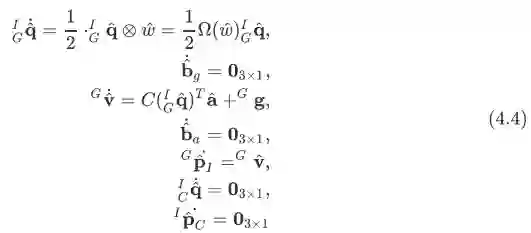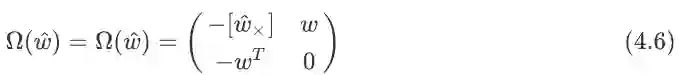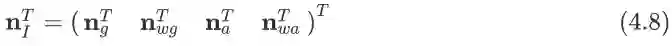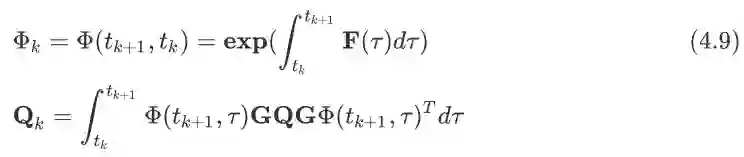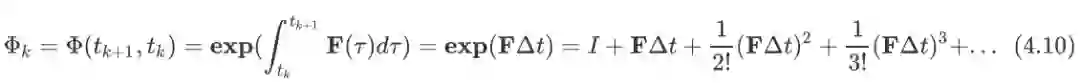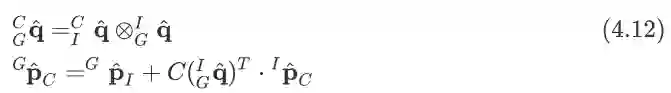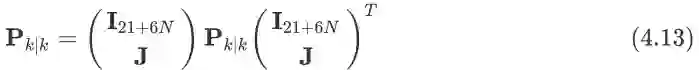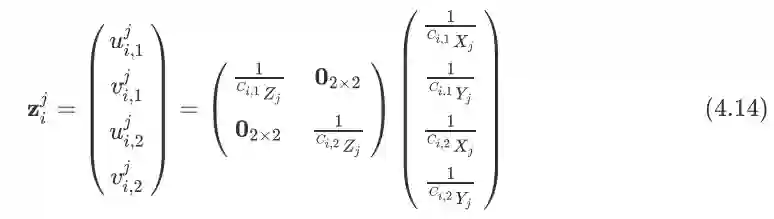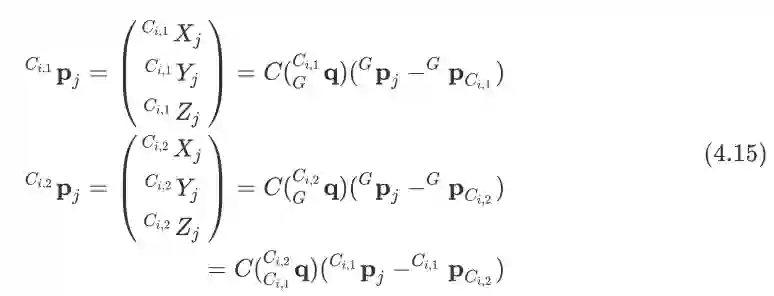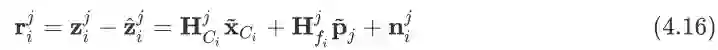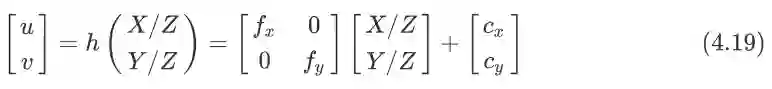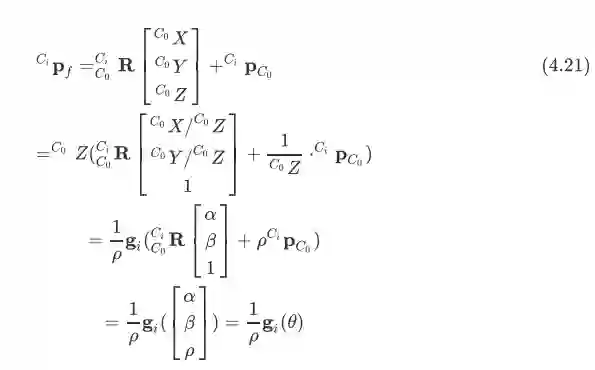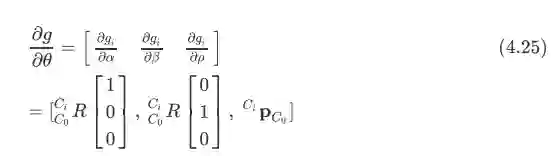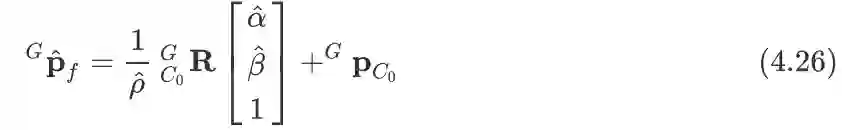【泡泡读者来稿】一步步深入了解S-MSCKF(二)
4.S-MSCKF
4.1 基本原理
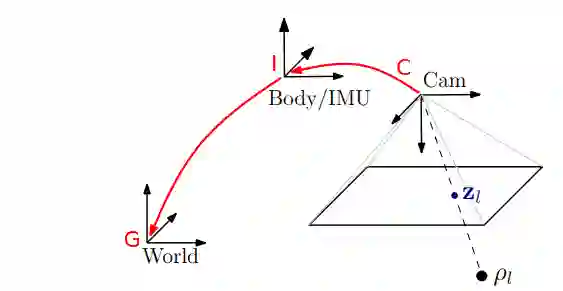
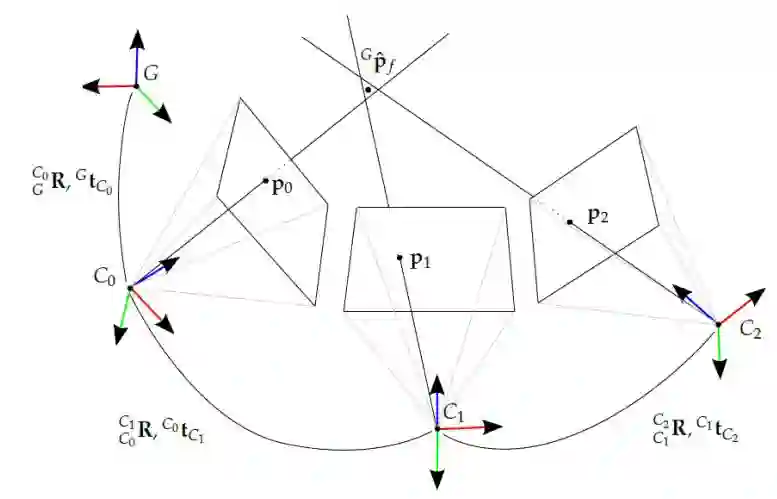
在讲解之前,我们先来定义一下坐标系,如下图所示:
其中表示IMU机体坐标系(Body Frame),
表示的是惯性系(Inertial Frame),
表示的是相机坐标系(Camera Frame).
作为一个滤波器,我们首先来看滤波器的状态向量,它包含两个部分,IMU状态和Camera状态:
其中表示的是从惯性系到机体IMU系的旋转变换,
和
分别表示机体在惯性系下的速度和位置,
和
分别代表IMU的bias,而
和
分别代表从相机坐标系到IMU坐标系的旋转与平移,其中以左相机为准. 但是我们注意到旋转实际上只有三个自由度,而且四元数必须是单位单位四元数,那这样额外的约束会使得协方差矩阵奇异,所以我们定义error IMU状态如下:
我们以标准error-state KF为准,其过程包含运动模型和观测模型.
A.运动模型
我们知道对于IMU的状态连续时间的运动学有:
其中 和
分别为角速度和加速度的估计值(测量值减去bias),即有:
其中有几点要说明,其中,
这个直接参考四元数乘法就可以了,然后是
的反对称矩阵;
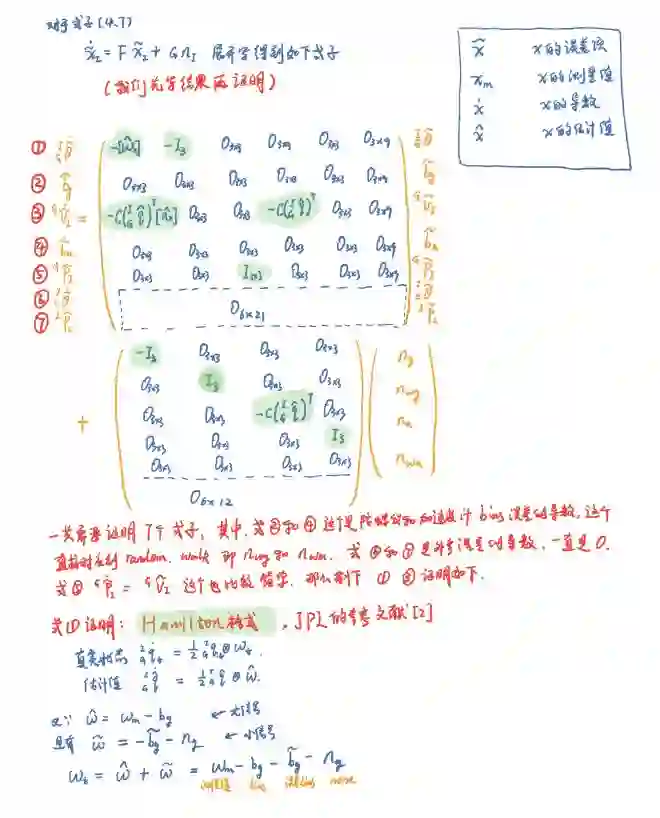
表示四元数到旋转矩阵的转换,这个可以参照[1]和[2]. 那按照S-MSCKF的论文所述,我们可以得到以下式子,
其中
和
分别代表角速度和加速度的测量噪声,服从高斯分布;
和
分别代表角速度和加速度的bias的随机游走噪声. F是21X21大小矩阵, G是21X12大小的矩阵,其详细推到见附录A.
对于IMU的状态来说,我们可以采用RK4的积分方法根据(4.4)求得IMU的状态. 那么对于IMU的协方差矩阵呢,我们需要事先求取状态转移矩阵和离散的运动噪声协方差矩阵,如下:
关于这个状态转移矩阵的求法, 其实式子4.9是一个指数,指数项是一个积分项,当
与
间
较小时候,可以得到这样的式子:
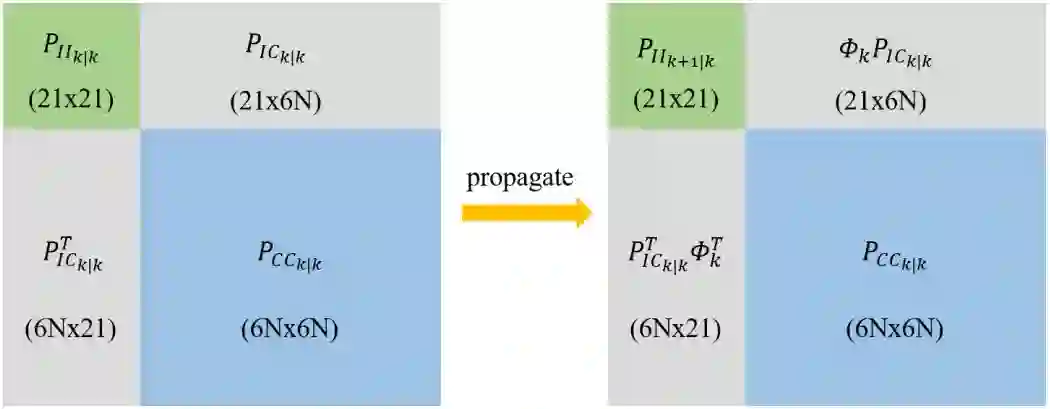
整个状态(IMU+Camera)的covariance传播过程如图所示:
那么对于左上角IMU的corvariance的传播有:
其中Camera的covariance暂时还没有变化是因为这个时间段图像还没有到来,只有IMU的影响,但是会影响到IMU与Camera协方差,即上图灰色矩形块.
B. 增广
当图像到来时,需要对当前相机姿态做增广,这个时刻的相机姿态是由上一时刻的IMU propagate的结果结合外参得到的:
假设上一时刻共有N个相机姿态在状态向量中,那么当新一帧图像到来时,这个时候整个滤波器的状态变成了的向量, 那么它对应的covariance维度变为
.其数学表达式为:
这个过程对应如下图过程:
其中的详细推导过程见附录B.
C.观测模型
MSCKF的观测模型是以特征点为分组的,我们可以知道一个特征(之前一直处于跟踪成功状态)会拥有多个Camera State.所有这些对于同一个3D点的Camera State都会去约束观测模型. 那这样其实隐式的将特征点位置从状态向量中移除,取而代之的便是Camera State. 我们考虑单个feture, 假设它所对应到
个相机姿态
. 当然双目版本的包含左目和右目两个相机姿态,
和
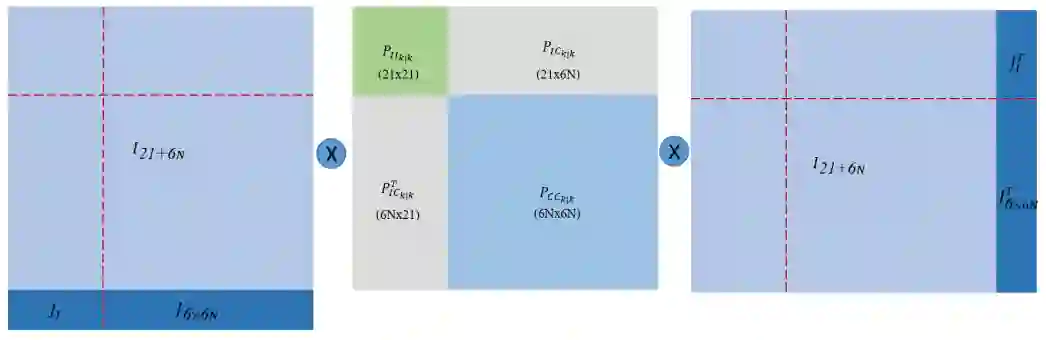
右相机很容易能通过外参得到. 其中双目的观测值可以表示如下:
而特征点在两个相机坐标系下可以分别表示为:
其中是特征点在惯性系下的坐标,这个是通过这个特征点的对应的所有camera state三角化得到的结果. 将观测模型在当前状态线性化可以得到如下式子:
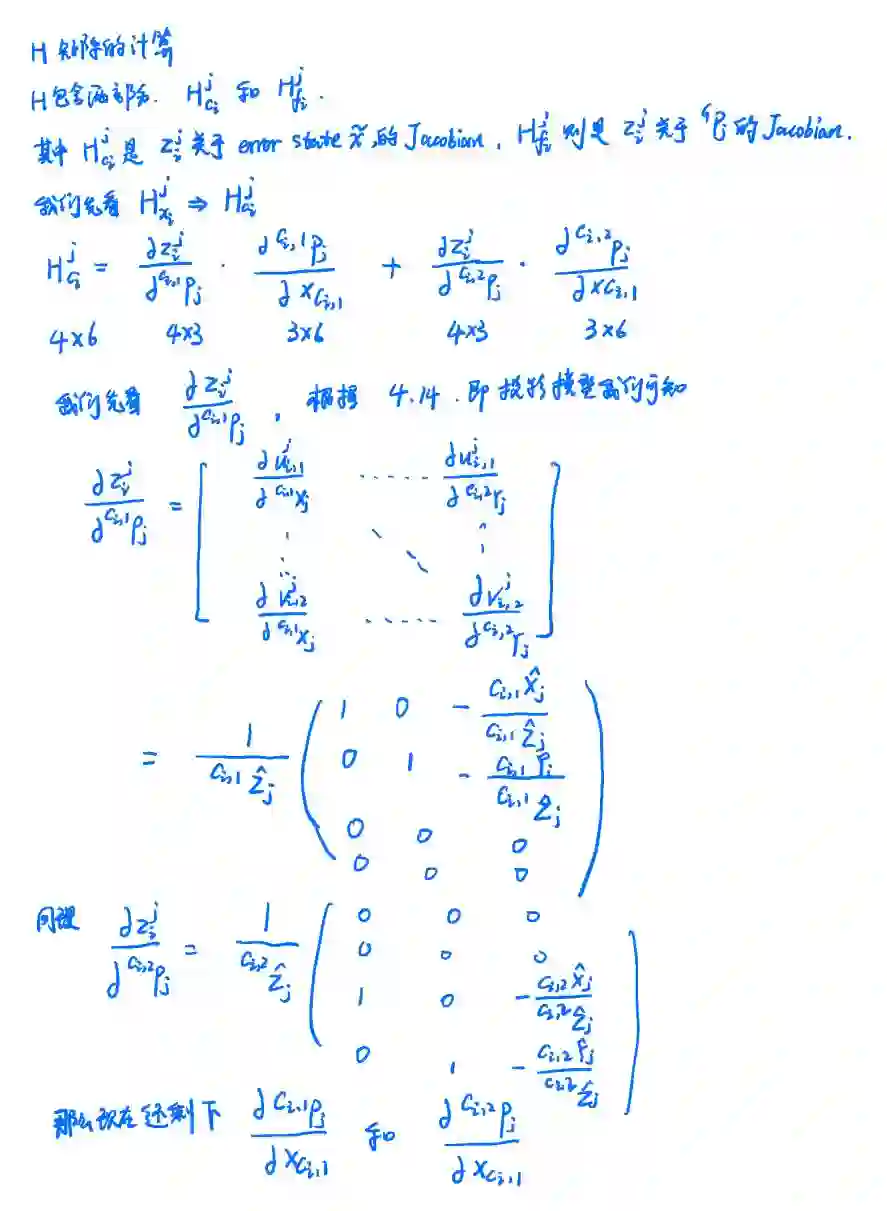
其中是观测噪声,
和
是对应的雅克比矩阵.其详细推导和解析见附录C. 式子(4.16)对应到的是单个特征点对应的其中某一个相机姿态, 但是这个特征点会对应到很多相机姿态,我们直接将它贴在后边可以得到一个特征点的残差模型为:
但是这个其实并不是一个标准的EKF观测模型,因为我们知道并不在我们的状态向量里边,所以做法是将式子(4.17)中红色部分投影到零空间, 假设
的left null space 为
, 即有
, 所以式(4.17)可有写成:
式(4.18)则是一个标准的EKF观测模型了,下面简单分析一下维度.分析时针对单个特征点, 我们知道的维度是
, 那么它的left null space的维度即
的维度为
, 则最终
的维度变为
, 残差的维度变为
, 假设一共有L个特征的话,那最终残差的维度会是
. 更多详细的代码细节见给到的注释版代码,然后H矩阵的详细推导见附录C.
4.2 三角化
三角化是通过多帧相机对同一个点的观测计算出特征点在世界坐标系下的绝对3D坐标,或者你可以认为是恢复出一个比较可靠的3D点. 在讲这个之前,我们先来简单过一下相机的投影模型, 假设相机图像已经去畸变了,那么我们很容易得到这样一个模型:
其中(X,Y,Z)为相机坐标系下的一个点. 我们再来看下图:
其中在惯性系下被多帧相机观测到,其中在每个相机下的坐标表示为
, 假设该特征第一个观测为
, 余数在第
个相机帧中可以表示为:
我们将这个转换为逆深度的表达形式,可以得到下面一系列式子:
其中为参数
,
,
.
并且这个假设我们的为
, 那么就是说
是一个3维输入,二维输出的函数. 所以误差函数可以写成:
假设一共共有N个相机观测,那么我们可以构建一个最小二乘问题,形如下式:
其中对应于单个特征点的jocabian形式如下:
其中第一项非常简单,就是参考式(4,19), 得到的结果第比较简单,第二部分
根据式子(4.21)可以很容易得到
然后用高斯-牛顿法就可以红容易解决这个最小二乘问题. 最后能得到, 那么其实也就是特征点在首个观测到它的相机帧下的坐标,根据下面的式子则很容易恢复出惯性系下的特征点的位置:
注意,代码中的实现和现在这个推到稍微有点出入,它的实现主要参考的是文献7,不过基本大同小异,大家阅读起来应该也不会有太大的阻碍.
4.3 能观测性分析
关于能观性分析,我个人感觉公式太多了,并且没有想到一个很好的描述方式,理解的也不算太透彻,所以这里还希望有大佬能把这部分写一下,或者单独写一个专题,我觉得那是极好的.
另外开源版本的S-MSCKF用的是OC-EKF, 这个主要参考了这两篇论文 Consistency Analysis and IMprovement of Vision-aided Inertial Navigation 和 On the consistency of Vision-aided Inertial Navigation. 代码中的实现主要参考了第二篇的给出的公式,我在注释里应该都有注明.
4.4 滤波器更新机制
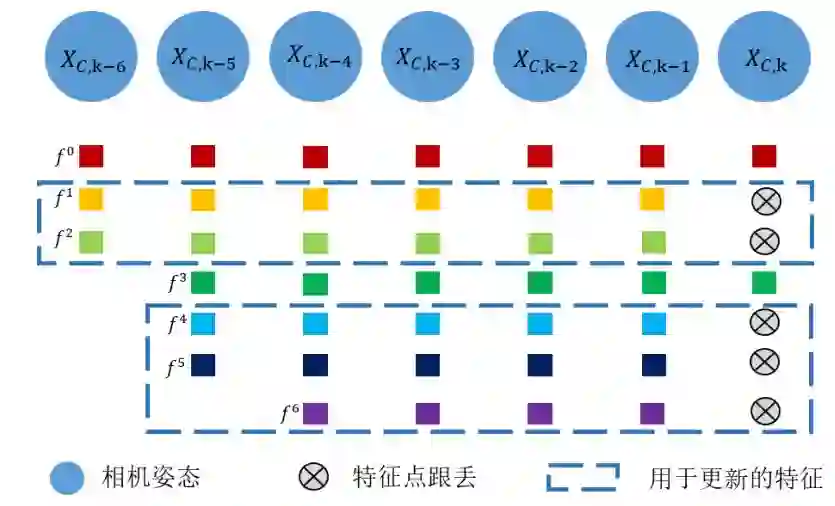
大致是有两种更新策略,假设新进来一帧图像,这个时候会丢失一些特征点,这个时候丢失的特征点(且三角化成功)用于滤波器更新,如下图所示:
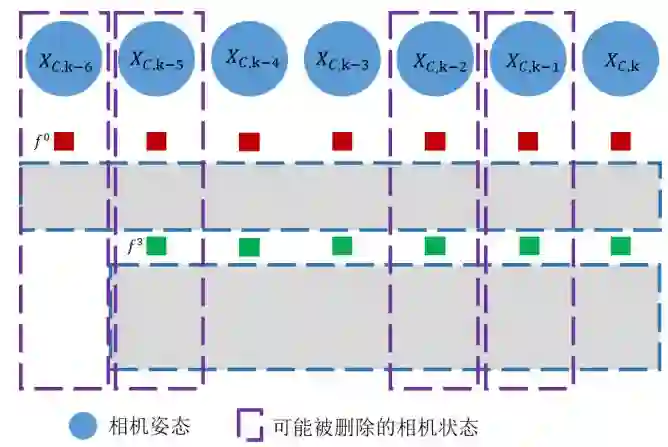
那当然随着时间的推移,相机状态会越来越多,这个时候呢, 相机状态会有一个阈值,也就是滑窗的上限, S-MSCKF与msckf1.0有稍微不同,它是当满了之后每次迭代的清除两个,最新的这个状态肯定保持, 清除依据就是帧间的旋转跟位移大小,如下图所示,假设Slide Window的大小正好为7,且已经经过了上面的update过程,那么这个时候还会再update一次,这个时候它的所有特征都会用于更新.因为要移除两个camera state,所以对应的状态和covariance也都需要剔除掉.所以删掉的两个状态其实肯定处于紫色框其中的两个.
5.S-MSCKF代码流程
这里放一张之前做的图,清晰图片从这里下载.另外中文注释版本的代码在这里
6.总结
全文以S-MSCKF为依托, 主要对MSCKF的理论基础和实现原理及细节进行了讲述, 并且对论文公式进行了详细的推导(很多手写的地方实在是不想敲了,太费时间了), 然后还对Quaternion kinematics for the error-state Kalman filter 这本书进行了详细的注释, 同时对开源版本的S-MSCKF的代码进行了注释. 由于笔者水平有限,有些地方理解难免不到位,其中就包括能观性分析这部分还没有做比较到位的解释,最后希望望读者批评指正文中不足的地方.
附录
A. F矩阵和G矩阵的推导
B. 的计算
的计算与正文有点出入,但还是先贴上来了,希望哪位大佬能推导得到论文的结果并告知我一下.
C. H矩阵
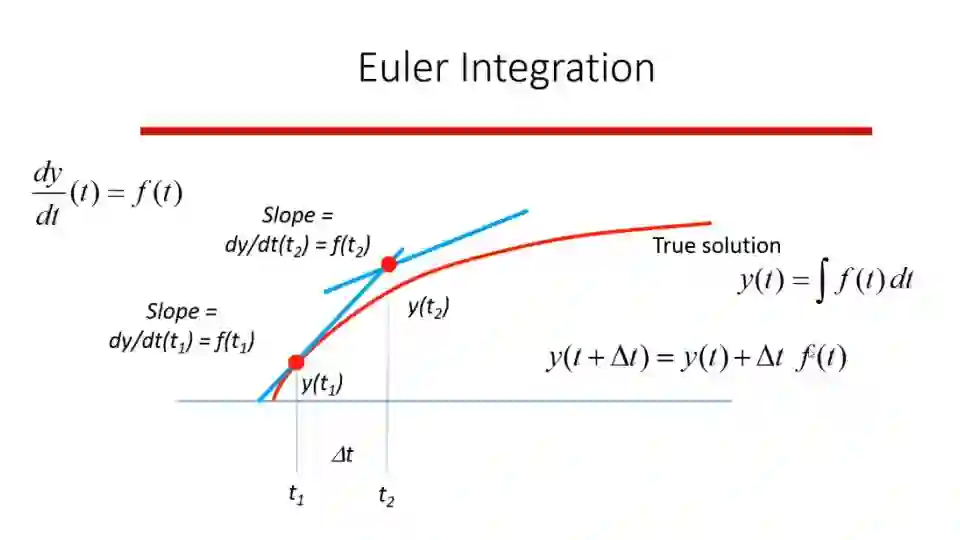
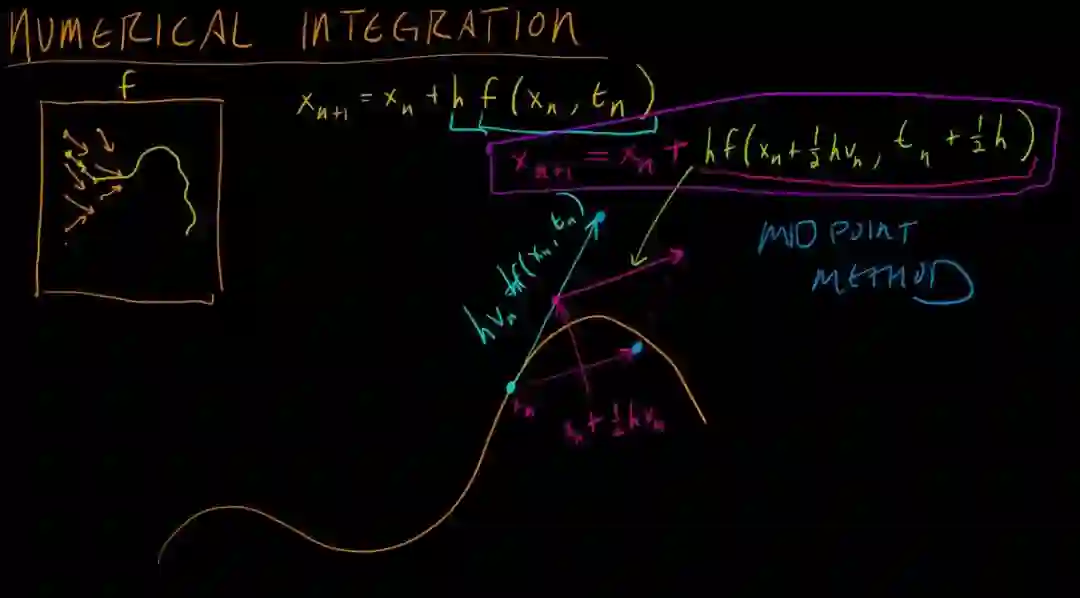
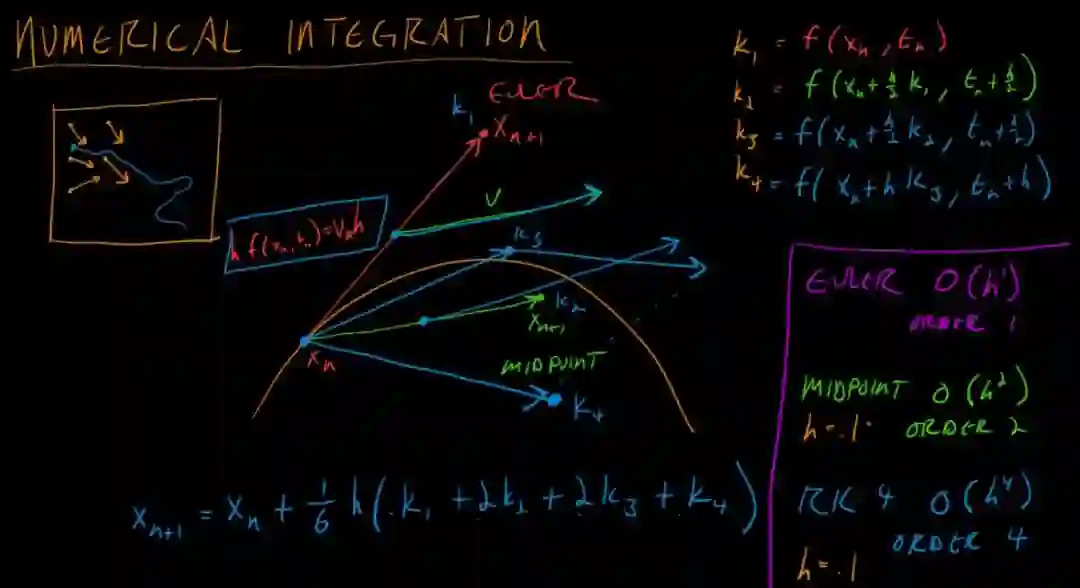
D. 三种常用数值积分方式:欧拉,中值,RK4积分
这部分其实比较简单, 大家也可以参考 参考文献1中附录A部分,也讲的很详细.这里简单附上三张图,分别对应三种积分方式.
7.参考文献
(1) Quaternion kinematics for the error-state Kalman filter
(2) Indirect Kalman Filter for 3D Attitude Estimation-A Tutorial for Quaternion Algebra
(3) Consistency Analysis and IMprovement of Vision-aided Inertial Navigation
(4) On the consistency of Vision-aided Inertial Navigation.
(5) Robust Stereo Visual Inertial Odometry for Fast Autonomous Flight
(6) Monocular Visual Inertial Odometry on a Mobile Device
(7) A multi-state constraint Kalman filter for vision-aided inertial navigation
(8) 视觉SLAM十四讲
(9) 卡尔曼滤波与组合导航原理