【泡泡读者来稿】VINS 论文推导及代码解析（四）

2019 年 3 月 17 日 泡泡机器人SLAM

崔华坤，SLAM算法工程师，主要研究方向是VIO。2011年硕士毕业于北京工业大学，毕业后从事六年的三维显示研发，从最初的裸眼3D显示到现在的AR显示，期间做出一款国内尺寸最大的裸眼3D LED屏。对作者感兴趣的可以加微信:cuihuakun。

7.闭环检测和优化

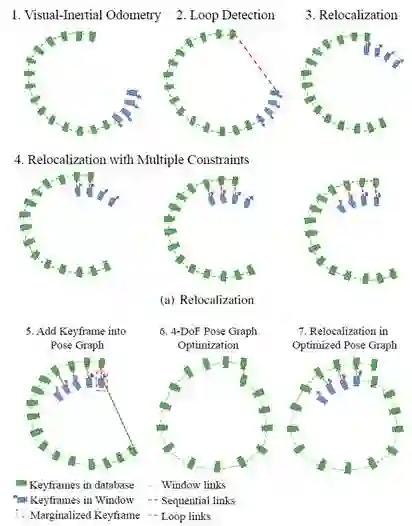
7.1 闭环检测

VINS是采用BRIEF描述子的DBoW2词袋进行闭环检测，因为前端识别的Harris角点数量通常只有70个（VINS-Mobile），对于闭环检测远远不够，因此会对新来的KeyFrame即后端非线性优化刚处理完的关键帧，再重新检测出500个FAST角点进行闭环检测用，同时对所有新老角点进行BRIEF描述（70个点的描述在computeWindowBRIEFPoint中，新的500个点在computeBRIEFPoint中，具体描述子代码在BriefExtractor::operator）。然后，将KF添加到数据中时（addKeyFrame），计算当前帧与词袋的相似度分数，并与关键帧数据库中所有帧进行对比，并进行闭环一致性检测，获得闭环的候选帧（detectLoop）。

当检测到闭环后，我们在findConnection函数中进行PnP求解相对位姿，首先利用BRIEF描述子对闭环对中老帧的500个FAST角点，和当前帧中的70个Harris角点进行基于描述子的邻域匹配（searchByBRIEF）；当匹配点数大于阈值后，将匹配点对利用PnPRANSAC求基础矩阵进行RANSAC异常点剔除，并求解相对位姿存储在loop_info变量中用于后续的闭环优化使用（为何求PnP时要用新帧的3D点，老帧的2D点呢？！），当剔除后的匹配点仍超过阈值时，我们最终认为该候选帧是一个正确的闭环帧，并将闭环帧push到optimize_buf中。

7.2 快速重定位

当检测到当前帧与之前帧（记为第v帧）有闭环时，若开启快速重定位，即FAST_RELOCALIZATION为true时，会将第v帧的位姿和相关特征点作为视觉约束项，加到后端非线性优化的整体目标函数中，但是并未固定第v帧的位姿，只是用滑窗优化来更精确计算第v帧的位姿，从而计算出闭环帧之间的相对位姿关系。这样的目标函数可写为：

b. 闭环边（Loop edge）：是指检测到闭环的两帧。

当运行时间越来越长，数据库将变得越来越大，导致闭环检测和闭环优化的耗时也将越来越长。虽然前面已经仅保留每帧图像的位姿和特征点描述子，已扔掉原始图像，但是当运行几小时后仍将无法实时。因此，我们将根据分布密度对数据库进行下采样，保留那些与周围帧的位置和角度不同的，而丢弃集中在一起的帧（代码对应KeyFrameDatabase::downsample）。

7.4 闭环优化

当从滑窗内滑出的帧与数据库中的帧为闭环帧时，则对数据库的所有帧进行闭环优化。因为前面已经跟重力对齐，因此根据重力方向可以观测出俯仰θ和翻滚ϕ角度，即pitch和roll可观。因此闭环优化时，我们仅优化位置x,y,z和偏航角yaw这四个自由度。

那么，第i帧和第j帧的残差可写成：

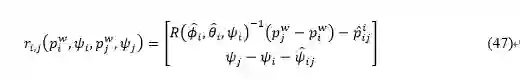
所有序列边和回环边的整体目标函数可写为：

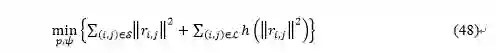
其中，S为序列边，L为回环边，h(.)为huber核函数。对应代码为KeyFrameDatabase::optimize4DoFLoopPoseGraph，注意代码中采用的Ceres自动求导方式。

到目前为止，我们就完成了对整个轨迹的闭环优化。

7.5 程序逻辑

下面我们对闭环与后端优化的关系再进行详细说明。

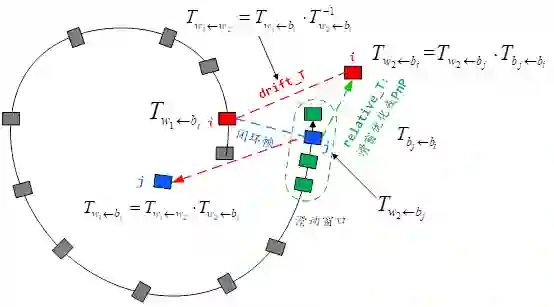
假设发生闭环的两帧为滑窗内的第j帧（蓝色帧），和数据库中的第i帧（红色帧）。令第i帧的位姿为T_(w_1←b_i )，第j帧的位姿为T_(w_2←b_j )，值得注意的是，两帧的世界系并不相同，滑窗所在的世界系w2为原世界系w1产生累积误差后的结果，重定位需要做的就是将w2改到w1。那么，根据PnP可得到两帧之间的相对位姿T_(b_j←b_i )，注意这里的PnP是用的第i帧的2D点和第j帧的3D点。但是PnP计算的相对位姿通常不准确，因此，可将PnP的结果作为初始值传到滑窗中，优化得到第i帧在世界系w2中的位姿T_(w_2←b_i )。为了将w2改到w1，我们计算累积偏移位姿：T_(w_1←w_2 )=T_(w_1←b_i )∙T_(w_2←b_i)^(-1)，这样的话，就可以将当前的第j帧重定位到原世界系中：T_(w_1←b_j )=T_(w_1←w_2 )∙T_(w_2←b_j )。如下图所示：

下图给出了闭环检测和优化的程序流程图：

上图中，蓝线为正常的闭环优化流程，即通过后端的非线性优化来更新滑窗内所有相机的位姿。紫线为闭环检测模块，当后端优化完成后，会将滑窗内的次新帧进行闭环检测，即首先提取新角点并进行描述，然后与数据库进行检索，寻找闭环帧，并将该帧添加到数据库中。红线为快速重定位模块，当检测到闭环帧后，会将闭环约束添加到后端的整体目标函数中进行非线性优化，得到第i帧（注意这里的帧为闭环帧中的老帧）经过滑窗优化后的位姿，从而计算出累积的偏移误差，进而对滑窗内的位姿进行修正。

这里，也可以在四自由度优化后PoseGraph::optimize4DoF()，将优化后的T_(w_1←w_2 )，即对应代码中的drift_correct_r、drift_correct_t，传回给后端优化线程，来更新滑窗内的相机位姿Estimator::update_loop_correction()。

8.其他

8.1 选KF策略

代码对应在addFeatureCheckParallax。

首先，迭代image即当前帧检测到的每个路标点id，看看图4中的feature队列中是否包含，若不含，则添加到feature队列中；若包含，则添加到对应id的FeaturePerFrame队列。

然后，compensatedParallax2计算每个路标点在两幅图中的视差量，若视差量大于某个阈值或者当前帧跟踪的路标点小于某个阈值，则边缘化滑窗内最老的帧；否则，边缘化掉次新帧，即倒数第二帧。

8.2 后端优化后的变量更新

代码对应：Estimator::double2vector()，其中rot_diff是根据滑窗中第一帧在优化前后的yaw偏差计算得到的旋转矩阵，之后对滑窗内所有帧都进行rot_diff的校正。这是因为在后端滑动窗口的非线性优化时，我们并没有固定住第一帧的位姿不变，而是将其作为优化变量进行调整。但是，因为相机的偏航角yaw是不可观测的，也就是说对于任意的yaw都满足优化目标函数，因此优化之后我们将偏航角旋转至优化前的初始状态。

8.3 丢失后多地图融合

当丢失后，会从丢失位置重新初始化，并将相机位姿Pose修正为上次修正完drift后的Pose，并将posegraph中的drift清零，就修改R_(b_j)^w为R_(b_j_drift)^w，并在此基础上进行闭环优化。

同时，每次跟丢后的地图记为新地图，并跟老地图一块放到datebase中进行闭环检测，只是sequence++，当闭环检测成功后，将新老地图进行对齐融合。

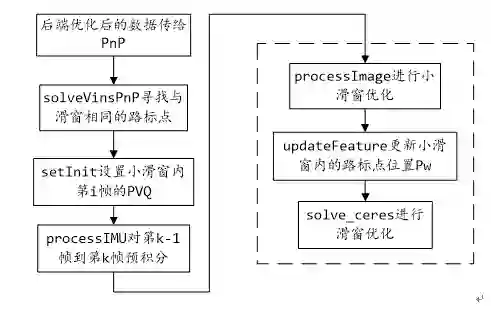
8.4 小滑窗PnP优化

为了控制后端滑窗优化的计算量，通常是每隔几帧（比如3帧）选一帧送到后端处理。为了计算被舍弃的帧的位姿，在VINS-Mobile版本中，加入了一种轻量级的基于小滑窗的PnP+IMU联合优化方案，对应在代码vins_pnp.cpp中。实现流程如下图所示：

1.当后端优化完成后，将滑窗内的最新帧（假设第i帧）的信息（时间戳、PVQ、bias）给到FeatureTracker的solved_vins，并将滑窗中所有的路标点信息（id、P_w、被观测到的次数）给到FeatureTracker的solved_features。另外，通过GetImuMeasurements()函数计算两帧之间的IMU数据，送给FeatureTracker的imu_msgs，注意这里的两帧是前端获得的最新帧（假设第k帧，注意k>i）和上一个连续帧之间。如下图所示：

2.FeatureTracker::solveVinsPnP()中寻找第k帧中与滑窗中相同的路标点，计算该路标点在归一化相机系中的坐标，传给feature_msg；

3. vinsPnP::setInit()对PnP的小滑窗（比如6个相邻帧）内的PVQB进行赋值，当小滑窗内有第i帧时，则用从后端传过来的第i帧PVQ来更新；

4. processImu是进行第k-1帧和第k帧的预积分；

5. processImage中首先通过updateFeatures更新小滑窗中与第k帧有共视关系的帧的3D点坐标P_w，最后调用solve_ceres来优化小滑窗内的PVQ，不优化路标点，涉及的两个约束为：IMU的帧间约束，和每一帧的PnP（即每一帧的2D-3D观测）的视觉重投影误差约束，因子图如下所示：

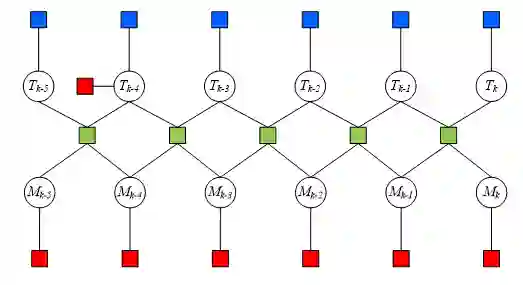
上图中，小方块为约束因子，圆圈为优化变量（这里路标点不是优化变量）：T=[R|t]，M=[v,b_a,b_w ]，绿色小块为IMU约束，蓝色小块为PnP视觉约束，红色小块为先验约束，比如第k-4帧对应后端大滑窗的第i帧，因此信赖并固定住第k-4帧的T_(k-4)和M_(k-4)；另外，固定住所有帧的bias。

9.参考文献

[1] T. Qin. VINS-Mono: A robust and versatile monocular visual-inertial state estimator. arXiv preprint arXiv: 1708.03852, 2017.

[2] N. Trawny. Indirect Kalman Filter for 3D Attitude Estimation. 2005.

[3] Sola. Quaternion kinematics for error-state kalman filter. 2017.

[4] K. Eckenhoff. Decoupled, Consistent Node Removal and Edge sparsification for graph-based SLAM. 2016.

[5] J. Engel. Direct Sparse Odometry. 2016.

[6] Sliding Window Filter with Application to Planetary Landing. 2010.

[7] S. Leutenegger. Keyframe-Based Visual-Inertial SLAM Using Nonlinear Optimization. 2015.

[8] “VINS-Mono代码分析总结”，https://www.zybuluo.com/Xiaobuyi/note/866099.

[9] 贺一家，“SLAM中的marginalization 和 Schur complement”，https://blog.csdn.net/heyijia0327/article/details/52822104.

请点击阅读原文获取完整解读！

欢迎来到泡泡论坛，这里有大牛为你解答关于SLAM的任何疑惑。