NeurIPS 2020 | 用于半监督学习的图随机神经网络
导读:在 NeurIPS 2020 上,清华大学联合微众银行、微软研究院以及博世人工智能中心提出了 Graph Random Neural Network (GRAND),一种用于图半监督学习的新型图神经网络框架。在模型架构上,GRAND 提出了一种简单有效的图数据增强方法 Random Propagation,用来增强模型鲁棒性及减轻过平滑。基于 Random Propagation,GRAND 在优化过程中使用一致性正则(Consistency Regularization)来增强模型的泛化性,即除了优化标签节点的 cross-entropy loss 之外,还会优化模型在无标签节点的多次数据增强的预测一致性。GRAND 不仅在理论上有良好的解释,还在三个公开数据集上超越了 14 种不同的 GNN 模型,取得了 SOTA 的效果。
这项研究被收入为 NeurIPS 2020 的 Oral paper (105/9454)。
论文名称:GraphRandom Neural Network for Semi-Supervised Learning on Graphs
ArXiv: https://arxiv.org/abs/2005.11079
Github: https://github.com/THUDM/GRAND
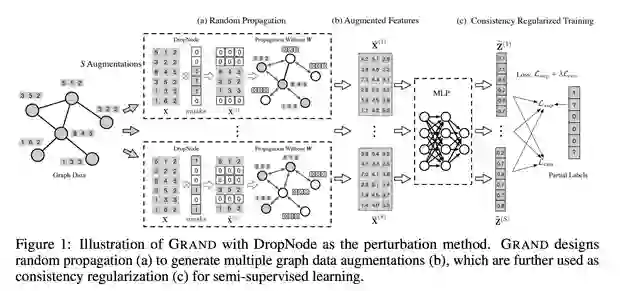
为了解决这些问题,在这个工作中我们提出了图随机神经网络(GRAND),一种简单有效的图半监督学习方法。与传统 GNN 不同,GRAND 采用随机传播 (Random Propagation)策略。具体来说,我们首先随机丢弃一些节点的属性对节点特征做一个随机扰动,然后对扰动后的节点特征做一个高阶传播。这样一来,每个节点的特征就会随机地与其高阶邻居的特征进交互,这种策略会降低节点对某些特定节点的依赖,提升模型的鲁棒性。
除此之外,在同质图中,相邻的节点往往具有相似的特征及标签,这样节点丢弃的信息就可以被其邻居的信息补偿过来。因此这样形成的节点特征就可以看成是一种针对图数据的数据增强方法。基于这种传播方法,我们进而设计了基于一致性正则(consistency regularization)的训练方法,即每次训练时进行多次 Random Propagation 生成多个不同的节点增强表示,然后将这些增强表示输入到一个 MLP 中,除了优化交叉熵损失之外,我们还会去优化 MLP 模型对多个数据增强产生预测结果的一致性。这种一致性正则损失无需标签,可以使模型利用充足的无标签数据,以弥补半监督任务中监督信息少的不足,提升模型的泛化能力,减小过拟合的风险。
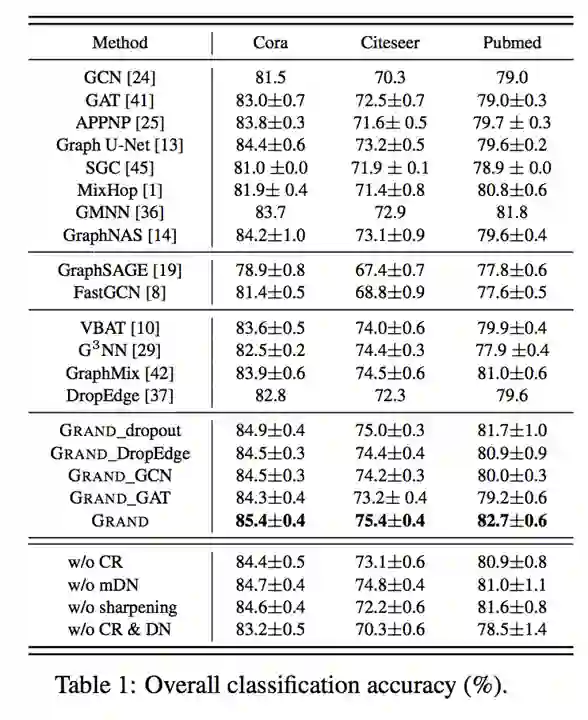
图三
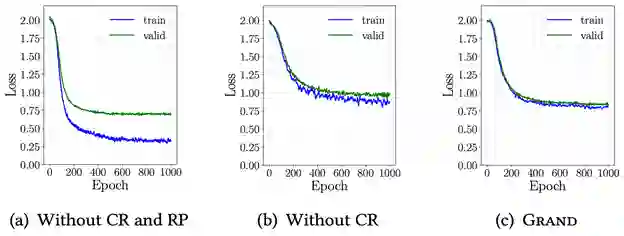
图四
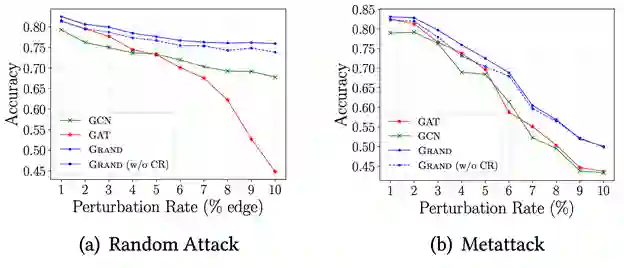
图五
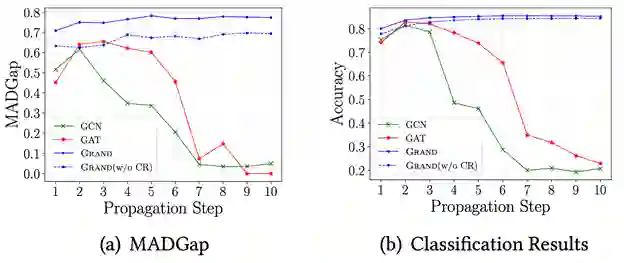
图六
[1] Kipf T N, Welling M. Semi-supervised classification with graph convolutional networks[J]. arXiv preprint arXiv:1609.02907, 2016.
[2] Zügner D, Akbarnejad A, Günnemann S. Adversarial attacks on neural networks for graph data[C]//Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. 2018: 2847-2856.