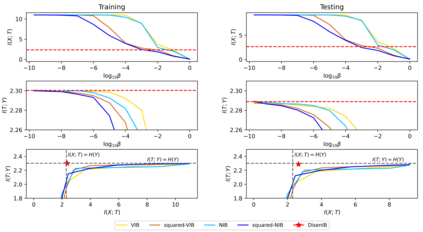
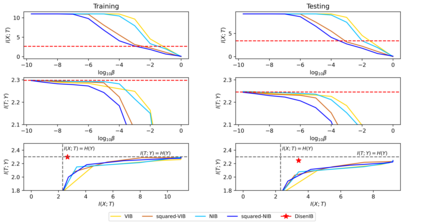
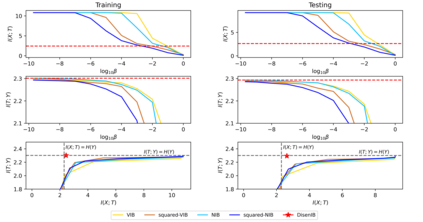
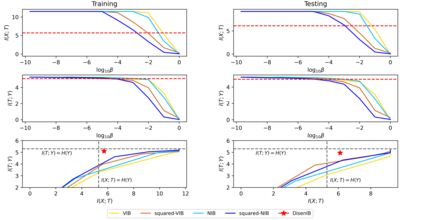
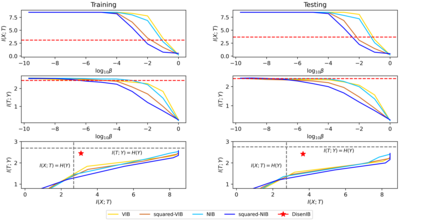
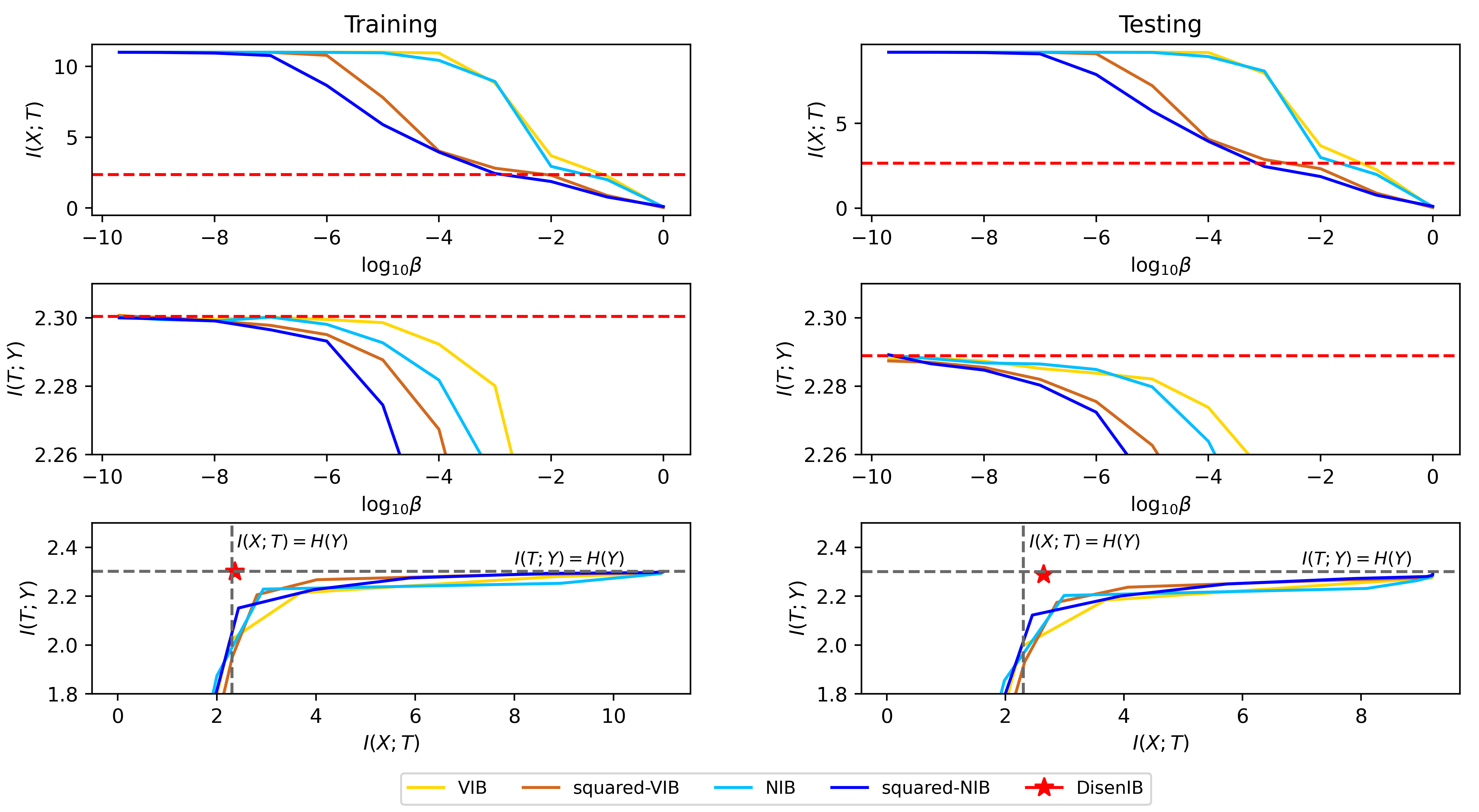
The information bottleneck (IB) method is a technique for extracting information that is relevant for predicting the target random variable from the source random variable, which is typically implemented by optimizing the IB Lagrangian that balances the compression and prediction terms. However, the IB Lagrangian is hard to optimize, and multiple trials for tuning values of Lagrangian multiplier are required. Moreover, we show that the prediction performance strictly decreases as the compression gets stronger during optimizing the IB Lagrangian. In this paper, we implement the IB method from the perspective of supervised disentangling. Specifically, we introduce Disentangled Information Bottleneck (DisenIB) that is consistent on compressing source maximally without target prediction performance loss (maximum compression). Theoretical and experimental results demonstrate that our method is consistent on maximum compression, and performs well in terms of generalization, robustness to adversarial attack, out-of-distribution detection, and supervised disentangling.
翻译:信息瓶颈(IB) 方法是一种从源随机变量中提取与预测目标随机变量相关的信息的技术,通常通过优化IB Lagrangian(IB Lagrangian)来实施,该方法平衡压缩和预测条件。然而,IB Lagrangian(IB)很难优化,需要多次测试拉格朗吉亚乘数的调值。此外,我们显示,随着压缩在优化 IB Lagrangian (IB) 时变得更强,预测性能将严格降低。 在本文中,我们从监督分解的角度实施IB(IB) 方法。 具体地说, 我们引入了分解信息瓶颈(DisenIB) 方法,该方法与压缩源一致,没有目标预测性效绩损失(最大压缩 ) 。 理论和实验结果表明,我们的方法与最大压缩一致,在一般化、 防御性攻击的强性、 分解检测和监督分解调方面表现良好。