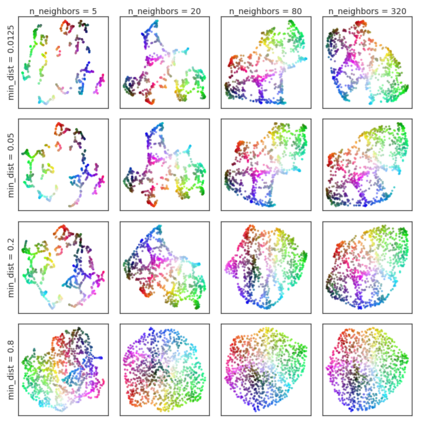
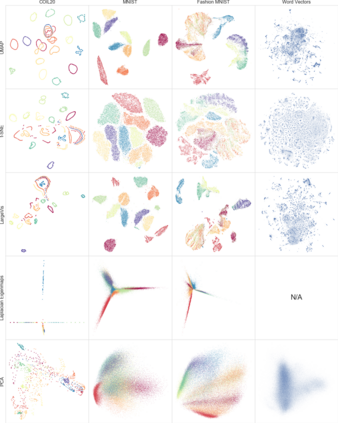
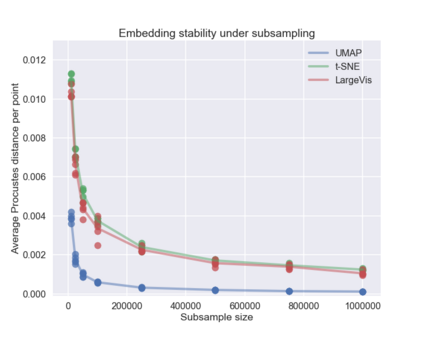
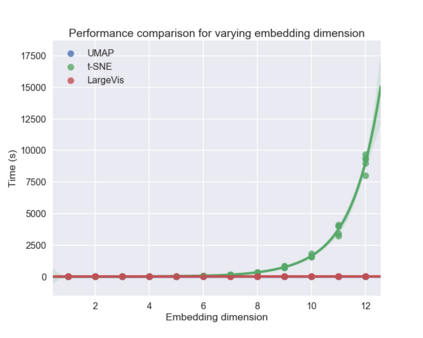
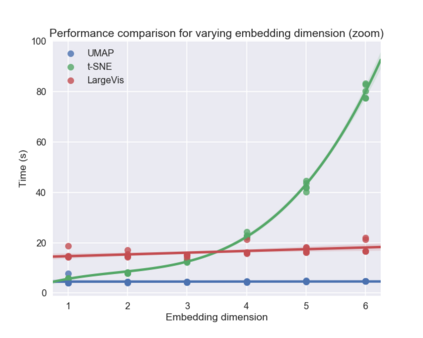
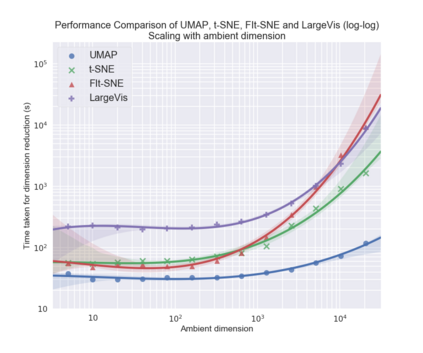
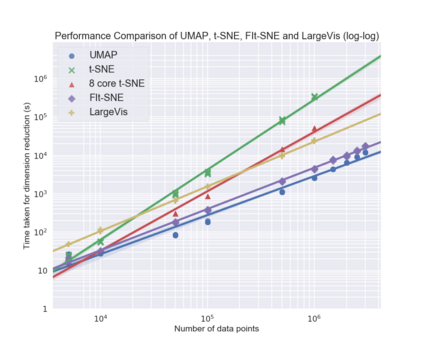
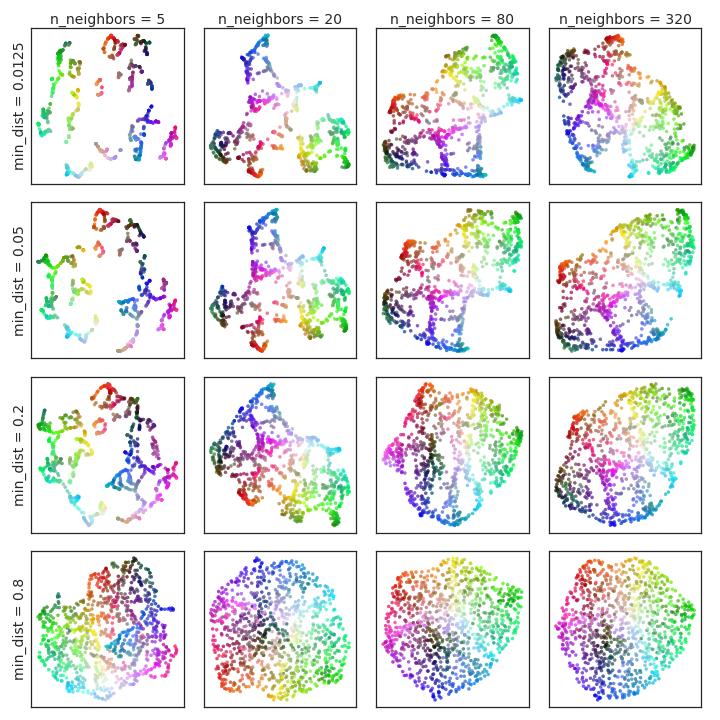
UMAP (Uniform Manifold Approximation and Projection) is a novel manifold learning technique for dimension reduction. UMAP is constructed from a theoretical framework based in Riemannian geometry and algebraic topology. The result is a practical scalable algorithm that applies to real world data. The UMAP algorithm is competitive with t-SNE for visualization quality, and arguably preserves more of the global structure with superior run time performance. Furthermore, UMAP has no computational restrictions on embedding dimension, making it viable as a general purpose dimension reduction technique for machine learning.
翻译:UMAP( UMAP ( Uniform Manifold Acceration and provision) 是用于降低维度的新颖的多种学习技术。 UMAP是根据基于里曼几何学和代数表层学的理论框架构建的。 其结果是适用于真实世界数据的实用可缩放算法。 UMAP算法在可视化质量方面与 t-SNE具有竞争力,而且可以说保留了更多的全球结构,具有较高的运行时间性能。 此外, UMAP在嵌入维方面没有计算限制,因此它作为机器学习的一般目的的减少维度技术是可行的。