【干货书】矩阵数学理论，事实和公式，第二版，1103页pdf

2005年首次出版时，《矩阵数学》迅速成为工程、科学和应用数学的所有分支中矩阵用户的必备参考书。在这个完全更新和扩展的版本中，作者汇集了矩阵理论的最新结果，使这成为矩阵上最完整的，当前的和易于使用的书。

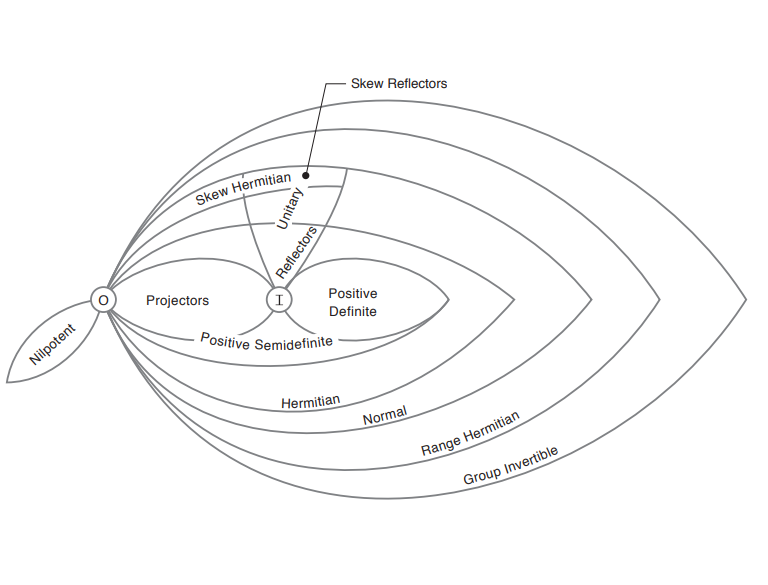
每一章都描述了相关的背景理论，然后是专门的结果。数以百计的恒等式、不等式和矩阵事实通过交叉引用、文献引用和启发性评论清楚而严格地陈述。从集合、函数和关系的初步开始，矩阵数学涵盖了矩阵理论中的所有主要主题，包括矩阵变换;多项式矩阵;矩阵分解;广义逆;Kronecker和Schur代数;半正定矩阵;向量和矩阵范数;矩阵指数与稳定性理论;线性系统和控制理论。还包括符号的详细列表，符号和惯例的摘要，广泛的参考书目和作者索引与页面引用，以及详尽的主题索引。这个显著扩展版的矩阵数学的特点在图上的新材料，标量恒等式和不等式，可选偏序，矩阵铅笔，有限组，多变量传递函数的零，多项式的根，凸函数，和矩阵规范。

涵盖了数以百计的矩阵理论的重要和有用的结果，许多以前从未在任何书中可用 提供符号列表和约定摘要，以方便使用 包括标量恒等式和不等式的广泛集合 功能一个详细的参考书目和作者索引与页面引用 包括一个详尽的主题索引与交叉引用