斯坦福开放新书《应用线性代数导论：向量、矩阵和最小二乘法》473页pdf，带你入门线代

【导读】斯坦福大学Stephen Boyd教授与加州大学Lieven Vandenberghe教授合著的应用线性代数导论：向量、矩阵和最小二乘法《Introduction to Applied Linear Algebra – Vectors, Matrices, and Least Squares》在2018年由剑桥大学出版社发行，开源书包含19章，473页pdf，这本书的目的是提供一个介绍向量，矩阵，最小二乘方法，应用线性代数的基本主题。目标是让学生通俗易懂，入门学习。让学习者了解在包括数据拟合、机器学习和人工智能,断层、导航、图像处理、金融、和自动控制系统的应用。是一本不可多得好教材。

作者介绍

Stephen P. Boyd是斯坦福大学电子工程Samsung 教授，信息系统实验室电子工程教授，斯坦福大学电子工程系系主任。他在管理科学与工程系和计算机科学系任职，是计算与数学工程研究所的成员。他目前的研究重点是凸优化在控制、信号处理、机器学习和金融方面的应用。

https://web.stanford.edu/~boyd/

Lieven Vandenberghe，美国加州大学洛杉矶分校电子与计算机工程系和数学系教授

Introduction to Applied Linear Algebra                          

– Vectors, Matrices, and Least Squares

新书地址：

https://web.stanford.edu/~boyd/vmls/

摘要：

这本书的目的是提供一个介绍向量，矩阵，最小二乘方法，应用线性代数的基本主题。我们的目标是让很少或根本没有接触过线性代数的学生快速学习,以及对如何使用它们在许多应用程序中, 包括数据拟合、机器学习和人工智能, 断层、导航、图像处理、金融、和自动控制系统。

读者所需要的背景知识是熟悉基本的数学符号。我们只在少数地方使用微积分，但它并不是一个关键的角色，也不是一个严格的先决条件。虽然这本书涵盖了许多传统上作为概率和统计的一部分来教授的话题，比如如何将数学模型与数据相匹配，但它并不需要概率和统计方面的知识或背景。

这本书涉及的数学比应用线性代数的典型文本还少。我们只使用线性代数中的一个理论概念，线性无关，和一个计算工具，QR分解;我们处理大多数应用程序的方法只依赖于一种方法，即最小二乘(或某种扩展)。从这个意义上说，我们的目标是知识经济:仅用一些基本的数学思想、概念和方法，我们就涵盖了许多应用。然而，我们所提供的数学是完整的，因为我们仔细地证明了每一个数学命题。然而，与大多数介绍性的线性代数文本不同，我们描述了许多应用程序，包括一些通常被认为是高级主题的应用程序，如文档分类、控制、状态估计和组合优化。

这本书分为三部分。 第一部分向读者介绍向 量 ，以及各种向量运算和函数，如加法、内积、距离和角度。 我们还将描述如何在应用程序中使用向量来表示文档中的字数、时间序列、病人的属性、产品的销售、音轨、图像或投资组合。 第二部分对矩阵也做了同样的处理 ，最终以矩阵的逆和求解线性方程的方法结束。 第三部分，关于最小二乘，是回报，至少在应用方面 。 我们展示了近似求解一组超定方程的简单而自然的思想，以及对这一基本思想的一些扩展，可以用来解决许多实际问题。

目录：

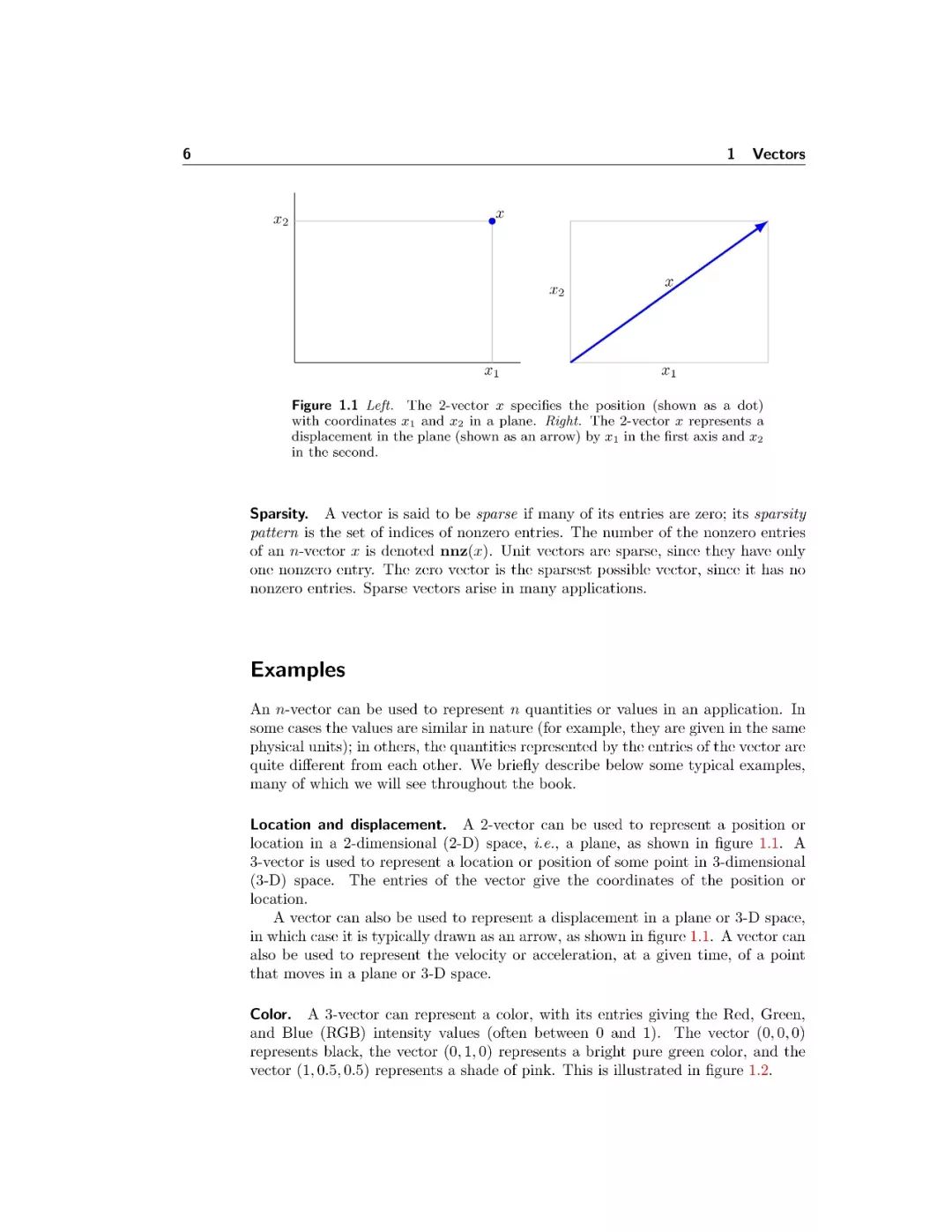
部分章节：

便捷下载：关注专知公众号（点击上方蓝色专知关注）

• 后台回复“VMLS” 获取《应用线性代数导论：向量、矩阵和最小二乘法》pdf链接下载索引~

-END-

专 · 知

专知，专业可信的人工智能知识分发，让认知协作更快更好！欢迎注册登录专知www.zhuanzhi.ai，获取5000+AI主题干货知识资料！

欢迎微信扫一扫加入专知人工智能知识星球群，获取最新AI专业干货知识教程视频资料和与专家交流咨询！

请加专知小助手微信（扫一扫如下二维码添加），获取专知VIP会员码，加入专知人工智能主题群，咨询技术商务合作~

点击“阅读原文”，了解成为 专知会员 ，查看5000+AI主题知识资料