ICML 2024 | 揭示非线形Transformer在上下文学习中学习和泛化的机制

转载机器之心：

本文作者李宏康，美国伦斯勒理工大学电气、计算机与系统工程系在读博士生，本科毕业于中国科学技术大学。研究方向包括深度学习理论，大语言模型理论，统计机器学习等等。目前已在 ICLR/ICML/Neurips 等 AI 顶会发表多篇论文。

上下文学习 (in-context learning, 简写为 ICL) 已经在很多 LLM 有关的应用中展现了强大的能力，但是对其理论的分析仍然比较有限。人们依然试图理解为什么基于 Transformer 架构的 LLM 可以展现出 ICL 的能力。

近期，一个来自美国伦斯勒理工大学和 IBM 研究院的团队从优化和泛化理论的角度分析了带有非线性注意力模块 (attention) 和多层感知机 (MLP) 的 Transformer 的 ICL 能力。他们特别从理论端证明了单层 Transformer 首先在 attention 层根据 query 选择一些上下文示例，然后在 MLP 层根据标签嵌入进行预测的 ICL 机制。该文章已收录在 ICML 2024。

论文题目：How Do Nonlinear Transformers Learn and Generalize in In-Context Learning? * 论文地址：https://arxiv.org/pdf/2402.15607

背景介绍

上下文学习 in context learning (ICL)

上下文学习 (ICL) 是一种新的学习范式，在大语言模型 (LLM) 中非常流行。它具体是指在测试查询 (testing query) 前添加 N 个测试样本 testing examples (上下文)，即测试输入 和测试输出 的组合，从而构成一个 testing prompt: ，作为模型的输入以引导模型作出正确的推断。这种方式不同于经典的对预训练模型进行微调的方式，它不需要改变模型的权重，从而更加的高效。

ICL 理论工作的进展

近期的很多理论工作都是基于 [1] 所提出的研究框架，即人们可以直接使用 prompt 的格式来对 Transformer 进行训练 (这一步也可以理解为在模拟一种简化的 LLM 预训练模式)，从而使得模型具有 ICL 能力。已有的理论工作聚焦于模型的表达能力 (expressive power) 的角度 [2]。他们发现，人们能够找到一个有着 “完美” 的参数的 Transformer 可以通过前向运算执行 ICL，甚至隐含地执行梯度下降等经典机器学习算法。但是这些工作无法回答为什么 Transformer 可以被训练成这样 “完美” 的，具有 ICL 能力的参数。因此，还有一些工作试图从 Transformer 的训练或泛化的角度理解 ICL 机制 [3,4]。不过，受制于分析 Transformer 结构的复杂性，这些工作目前止步于研究线性回归任务，而所考虑的模型通常会略去 Transformer 中的非线形部分。

本文从优化和泛化理论的角度分析了带有非线性 attention 和 MLP 的 Transformer 的 ICL 能力和机制：

基于一个简化的分类模型，本文具体量化了数据的特征如何影响了一层单头 Transformer 的域内 (in-domain) 和域外 (out-of-domain, OOD) 的 ICL 泛化能力。 * 本文进一步阐释了 ICL 是如何通过被训练的 Transformer 来实现了。 * 基于被训练的 Transformer 的特点，本文还分析了在 ICL 推断的时候使用基于幅值的模型剪枝 (magnitude-based pruning) 的可行性。

理论部分

问题描述

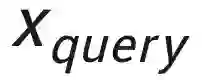
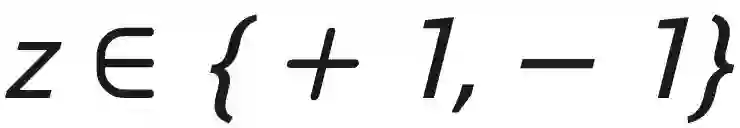
本文考虑一个二分类问题，即将 通过一个任务 映射到 。为了解决这样的一个问题，本文构建了 prompt 来进行学习。这里的 prompt 被表示为：

训练网络为一个单层单头 Transformer：

预训练过程是求解一个对所有训练任务的经验风险最小化 (empirical risk minimization)。损失函数使用的是适合二分类问题的 Hinge loss，训练算法是随机梯度下降。

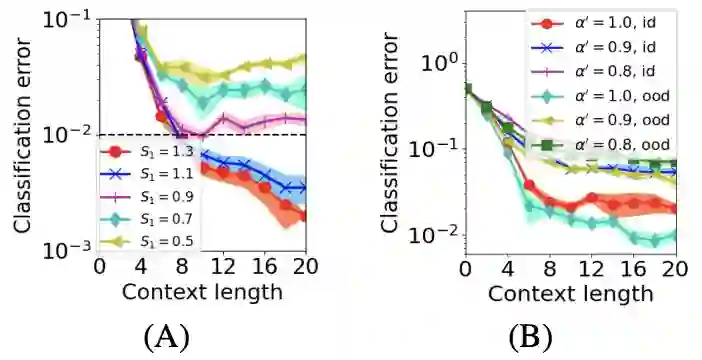
本文定义了两种 ICL 泛化的情况。一个是 in-domain 的，即泛化的时候测试数据的分布和训练数据一样，注意这个情况里面测试任务不必和训练任务一样，即这里已经考虑了对未见任务 (unseen task) 的泛化。另一个是 out-of-domain 的，即测试、训练数据分布不一样。

本文还涉及了在 ICL 推断的时候进行 magnitude-based pruning 的分析，这里的剪枝方式是指对于训练得到的中的各个神经元，根据其幅值大小，进行从小到大的删除。

对数据和任务的构建

这一部分请参考原文的 Section 3.2，这里只做一个概述。本文的理论分析是基于最近比较火热的 feature learning 路线，即通常将数据假设为可分（通常是正交）的 pattern，从而推导出基于不同 pattern 的梯度变化。本文首先定义了一组 in-domain-relevant (IDR) pattern 用于决定 in-domain 任务的分类，和一组与任务无关的 in-domain-irrelevant (IDI) pattern，这些 pattern 之间互相正交。IDR pattern 有 个，IDI pattern 有 个。一个 被表示为一个 IDR pattern 和一个 IDI pattern 的和。一个 in-domain 任务就被定义为基于某两个 IDR pattern 的分类问题。

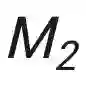
类似地，本文通过定义 out-of-domain-relevant (ODR) pattern 和 out-of-domain-irrelevant (ODI) pattern，可以刻画 OOD 泛化时候的数据和任务。

本文对 prompt 的表示可以用下图的例子来阐述，其中 是 IDR pattern， 是 IDI pattern。这里在做的任务是基于 x 中的 做分类，如果是 那么其标签为 + 1，对应于 +q，如果是 那么其标签为 - 1，对应于 -q。α，α' 分别被定义为训练和测试 prompt 中跟 query 的 IDR/ODR pattern 一样的上下文示例。下图中的例子里面， 。

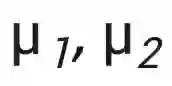
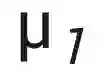
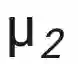
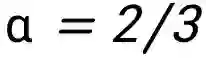
理论结果

首先，对于 in-domain 的情况，本文先给了一个 condition 3.2 来规定训练任务需要满足的条件，即训练任务需要覆盖所有的 IDR pattern 和标签。然后 in-domain 的结果如下：

这里表明：1，训练任务的数量只需要在全部任务中占比达到满足 condition 3.2 的小比例，我们就可以对 unseen task 实现很好的泛化；2，跟当前任务相关的 IDR pattern 在 prompt 中的比例越高，就可以以更少的训练数据，训练迭代次数，以及更短的 training/testing prompt 实现理想的泛化。

接下来是 out-of-domain 泛化的结果。

这里说明，如果 ODR pattern 是 IDR pattern 的线性组合且系数和大于 1，那么此时 OOD ICL 泛化可以达到理想的效果。这个结果给出了在 ICL 的框架下，好的 OOD 泛化所需要的训练和测试数据之间的内在联系。该定理也通过 GPT-2 的实验得到了验证。如下图所示，当 (12) 中的系数和 大于 1 的时候，OOD 分类可以达到理想的结果。与此同时，当 ，即 prompt 中和分类任务相关的 ODR/IDR pattern 比例越高的时候，所需要的 context 长度越小。

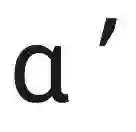
然后，本文给出了带有 magnitude-based pruning 的 ICL 泛化结果。

这个结果表明，首先，训练得到的 中有一部分（常数比例）神经元的幅值很小，而剩下的相对比较大（公式 14）。当我们只枝剪小神经元的时候，对泛化结果基本没有影响，而当枝剪比例增加到要剪大神经元的时候，泛化误差会随之显著变大（公式 15，16）。以下实验验证了定理 3.7。下图 A 中浅蓝色的竖线表示训练得到的 呈现出了公式 14 的结果。而对小神经元进行枝剪不会使泛化变差，这个结果符合理论。图 B 反映出当 prompt 中和任务相关的上下文越多的时候，我们可以允许更大的枝剪比例以达到相同的泛化性能。

ICL 机制

通过对预训练过程的刻画，本文得到了单层单头非线性 Transformer 做 ICL 的内在机制，这一部分在原文的 Section 4。该过程可以用下图表示。

简而言之，attention 层会选择和 query 的 ODR/IDR pattern 一样的上下文，赋予它们几乎全部 attention 权重，然后 MLP 层会重点根据 attention 层输出中的标签嵌入来作出最后的分类。

总结

本文讲解了在 ICL 当中，非线性 Transformer 的训练机制，以及对于新任务和分布偏移数据的泛化能力。理论结果对于设计 prompt 选择算法和 LLM 剪枝算法有一定实际意义。

参考文献 [1] Garg, et al., Neurips 2022. "What can transformers learn in-context? a case study of simple function classes." [2] Von Oswald et al., ICML 2023. "Transformers learn in-context by gradient descent." [3] Zhang et al., JMLR 2024. "Trained transformers learn linear models in-context." [4] Huang et al., ICML 2024. "In-context convergence of transformers."