【ICML2022】深入研究置换敏感的图神经网络

深入研究置换敏感的图神经网络

论文链接： https://www.zhuanzhi.ai/paper/da818de2d710f7cb9087582587f6240f 代码链接： https://github.com/zhongyu1998/PG-GNN 演示链接： https://github.com/zhongyu1998/PG-GNN/blob/main/demo.mp4

图与邻接矩阵的置换不变性是图神经网络（GNN）的首要要求，传统模型通过置换不变的聚合操作来满足这一前提条件。然而，这种高度对称的置换不变聚合方式假定所有邻居结点的地位均等，可能会忽略邻居结点与邻居结点之间的相互关系，进而阻碍 GNN 的表达能力。

与置换不变相反，置换敏感的聚合函数对于结点顺序非常敏感，可以看作是一种“对称性破缺”机制，打破了邻居结点的均等地位。这样一来，聚合函数可以显式地建模邻居结点之间的内在关系（如二元依赖），捕获两个邻居结点之间是否存在连接，从而识别并利用局部的图子结构来提高表达能力。

尽管置换敏感的聚合函数比置换不变的聚合函数具有更加强大的表达能力，但是还需要额外考虑所有n!种置换来保证泛化能力，在计算复杂度上面临着巨大的挑战。为了解决这一问题，本文利用置换群（permutation group）设计了一种新颖的置换敏感聚合机制，通过置换采样策略采样少量具有代表性的置换，捕获邻居与邻居之间的二元依赖，从而高效地提升 GNN 的表达能力：研究员们证明了所提出的方法严格地比二维 Weisfeiler-Lehman（2-WL）图同构测试更强大，并且能够区分一些 3-WL 测试无法区分的非同构图对；此外，相比于传统方法需要考虑所有 n! 种置换，本文所提出的方法能够达到线性的置换采样复杂度。

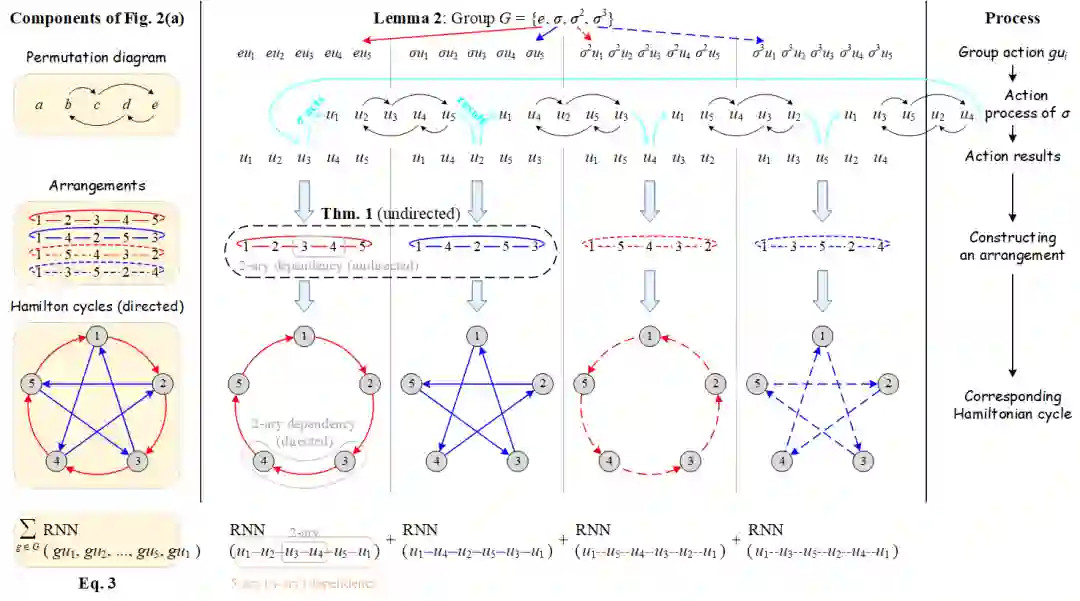
图2：考虑中心结点 v 和5个邻居结点的简单模型示例

综合而言，本文基于置换敏感的聚合机制设计了一种强大而高效的图神经网络，它在保证表达能力的同时，先后借助近似置换不变性的思想与线性置换采样策略，显著降低了计算复杂度。如何利用置换敏感的图神经网络在表达能力上的天然优势，在表达能力和计算复杂度之间寻找均衡，将是未来富有前景的研究方向。