会员服务 ·

陈政道：什么样的图神经网络更具表达能力？

2022 年 1 月 5 日 专知

分享嘉宾：陈政道纽约大学博士生

编辑整理：薛国潼武汉大学

出品平台：DataFunTalk

导读：我们最近研究的题目是探索图神经网络的表达能力，希望从理论上来理解图神经网络有哪些事情是能做的，哪些是不能做的，以此来比较不同的图神经网络模型，并提出一些更具表达能力的模型。

今天的探讨主要围绕以下3点展开：

图神经网络（GNN）简介
GNN表达能力的衡量
Graph-Augmented MLP

图神经网络（GNN）简介

1. 图神经网络（GNN）

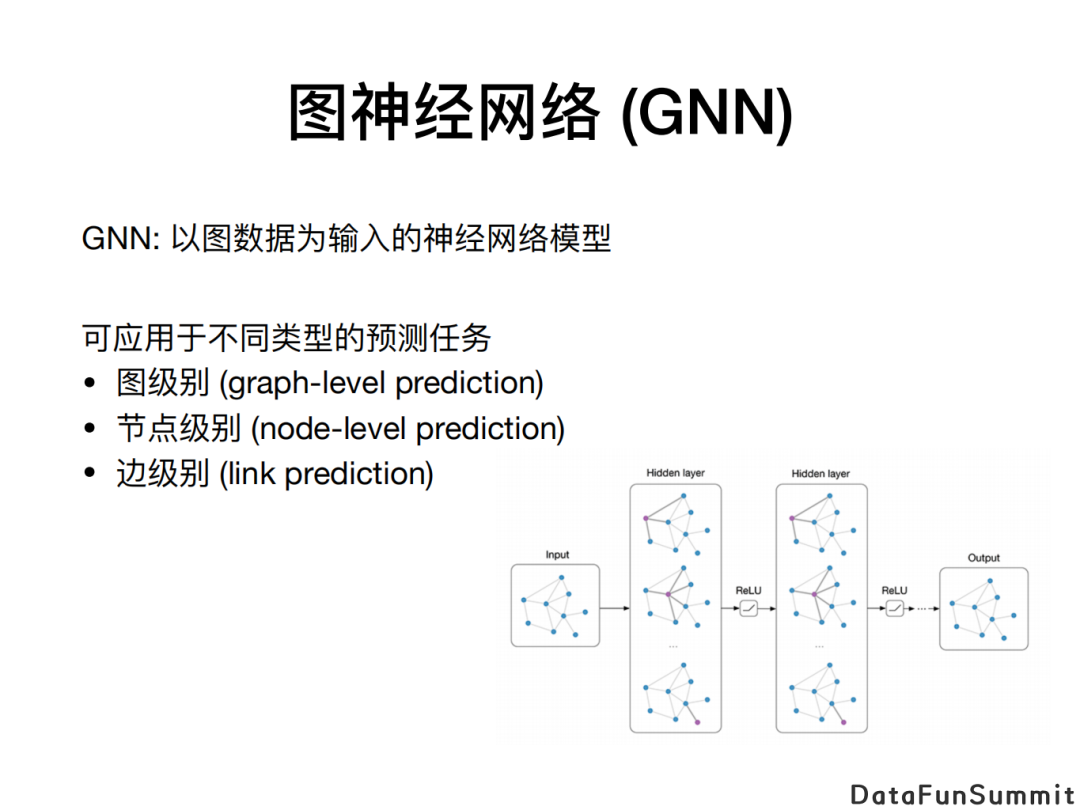
我们知道图神经网络(GNN)可以被用到不同类型的预测任务上，如图级别(graph-level)、节点级别(node-level)、或者边级别(edge-level)的任务。在图级别的预测任务中，我们可以把GNN视作一类用于图上的函数，它的输入是一个图，且图的节点或边上可能含有特征(features)。以分子预测为例，将分子视作图，可通过GNN将之映射为一个实数，这个实数可以代表该分子的某个化学性质，例如毒性或水溶性。

所以我们研究图神经网络的表达能力，也就是研究它作为一类用于图上的函数能有多强的表达能力来逼近图上的各类函数。

2. Message Passing NN（MPNN）

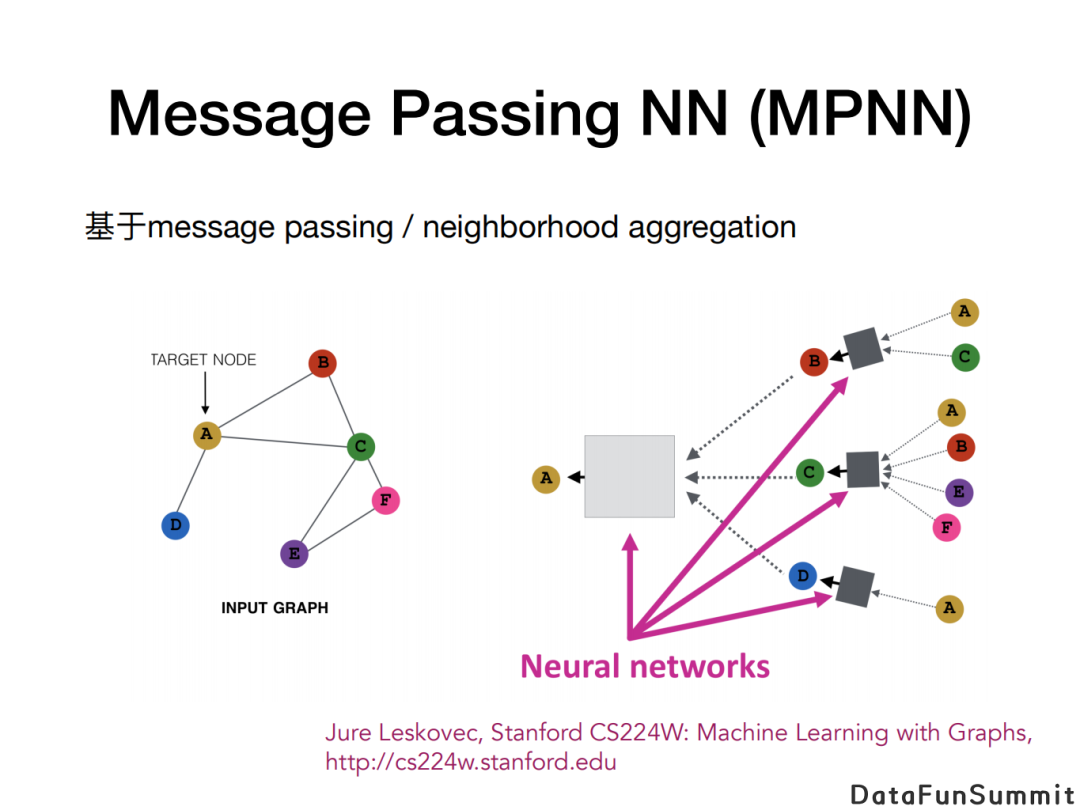
以常见的消息传播网络(Message Passing Neural Network, MPNN)为例，其核心思想是迭代更新节点的嵌入向量(embedding vector)。更新的方式是，首先每个节点会收到来自于它邻居节点传来的消息(message)，再对所收到的信息做聚合(aggregation)，以此来更新自身的嵌入向量。神经网络既参与第一步生成消息的过程，又参与之后更新节点的嵌入向量的过程。当使用不同的神经网络模型作为消息生成函数和节点更新函数时，便可得到不同种类的MPNN模型。

3. 理解图神经网络

GNN有一些好的性质：

满足对称性。如果对图的节点做置换(permutation)的话，GNN作为一个图上的函数，它的输出不会改变；
计算高效。消息传播是发生在局部的过程，有专门的实现方法来提升计算效率；
Inductive generalization。GNN可以在一个图上训练，然后在另一个图上做预测；
可训练+强表达能力。由于神经网络有很多参数可训练，所以其有能力表达复杂的函数。同时它具备好的优化性质，使得它可以基于数据训练来逼近的目标函数。

我们想研究的问题，是GNN的表达能力究竟如何。我们知道，前馈神经网络的表达能力常常是由它的宽度来限制。而图神经网络不只是受宽度限制，它本身如何利用图的拓扑进行消息传播与节点更新都会影响表达能力。我们希望对表达能力有一个理论上的理解，以此来比较不同的图神经网络模型，并且尝试去开发更有表达能力的模型。

GNN表达能力的衡量

1. 什么是图神经网络的表达能力

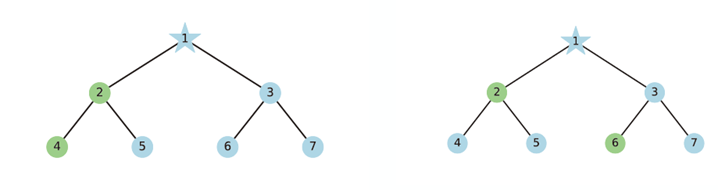
究竟什么是图神经网络表达能力，本身就是一个很好的问题。目前也有很多衡量表达能力的方法，如GNN能不能区分非同构图。以上两个图是非同构的，已有文章证明了MPNN无法区分这两个图，即，对任何一个MPNN，当我们把它作为一个图上的函数应用在这两个图上的时候，一定会得到相等的输出。

更一般性的结论是：MPNN区分同构图的能力最多等价于Weisfeiler-Lehman (WL)测试。许多工作基于此结论提出新模型，包括GIN，它使用单射(injective)的函数来做邻居信息的聚合，使得MPNN的表达能力在区分非图同构图上能够达到WL测试的能力。

2. 2-Invariant Graph Network（2-IGN）模型

我们关心的一个问题是在MPNN之外，其他类型的GNN在区分非同构图上拥有怎样的表达能力？

其中一个我们感兴趣的模型是Invariant Graph Network(IGN)。此类模型基于等变线性层(equivariant linear layer)和非线性激活函数的层层叠加。

假如图有N个节点，那么我们考虑从N^2维度的欧几里得空间到它自身的满足等变性的线性映射空间。研究发现所有这个函数空间的维度与N无关，且正好为15维的。相当于我们可以找到15个等变线性函数作为基底，可用它来参数化一个等变线性层，然后可以通过数据来对这些参数进行学习。这样通过叠加非线性激活函数，我们得到2-IGN模型。

2-IGN模型存在global信息传递，而不再是基于邻居节点之间的局部的消息传播，因而有可能有超出MPNN的表达能力。但我们也证明这一类2-IGN模型在区分非同构图的能力上和2-WL测试是等价的，也就是只有有限的区分非同构图的能力。

3. 构造表达能力更强的模型

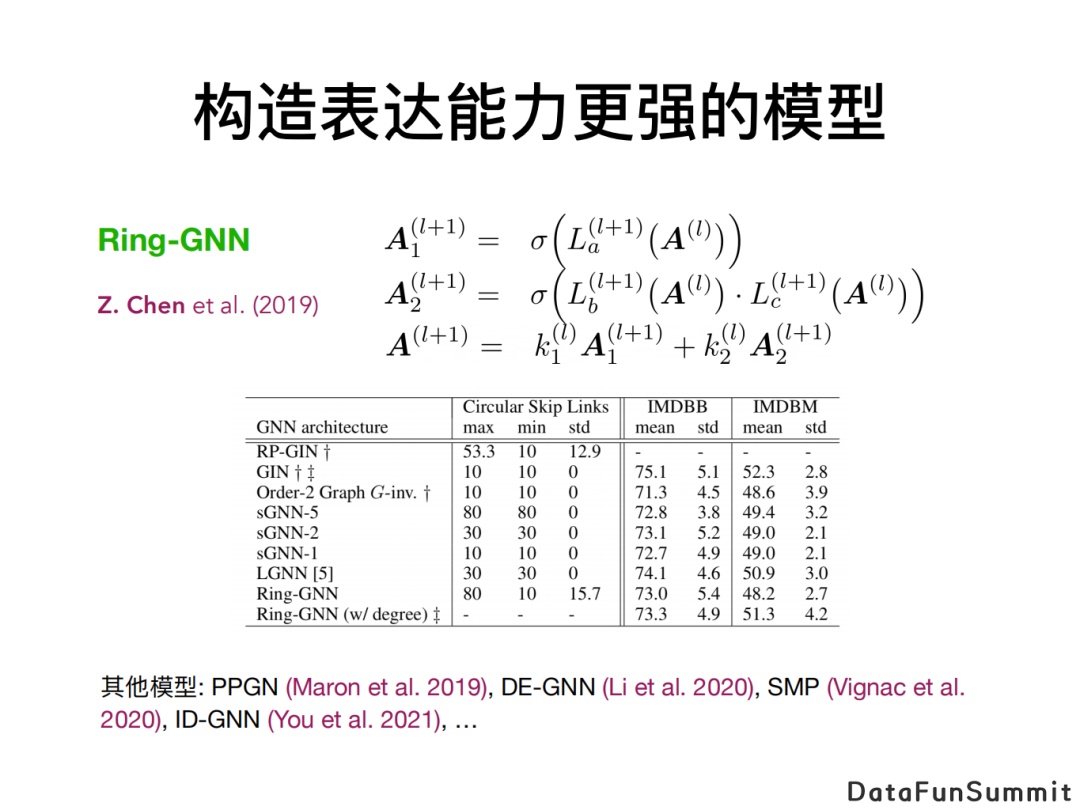
之后我们提出了一个更具表达能力的模型。在2-IGN的想法（也就是对等变线性层和非线性激活函数进行层层叠加）的基础上，我们增加了矩阵乘法的步骤。这个模型我们把它叫作Ring-GNN，名字来源于我们想基于加法与乘法构成一个图算子的环(ring)。我们在理论上证明Ring-GNN可以区分此前示例的两个非同构图。实验也表明它在区分一些非同构图上的效果强于其他的GNN模型。

近来也有很多其他的基于和WL测试对比的工作，包括Maron等人的PPGN模型，李攀等人的DE-GNN模型, Vignac等人的SMP模型，和尤佳轩等人的ID-GNN模型等。总之这是一个有趣的方向，以一种由理论支撑的方式来构造更强的模型。

4. 其他衡量表达能力的标准

经过以上的探讨，也许我们会疑惑，判断GNN能否区别非同构图在多大程度上是有意义的？如果我们发现模型无法区分某两个非同构图的话，对我们实际的应用有怎样的指导性价值？因为现实中的任务并非一定要区分非同构图。因此，我们希望找到一个更直观、具体、并和实际应用更加相关的标准来衡量GNN的表达能力。

因此，我们提出用能否对子图进行计数来衡量GNN表达能力。如果我们考虑分子预测的情景，有机分子的许多性质都由官能团来决定，而官能团就可看作分子中某一些原子的组合，即分子图的子图。除了在分子预测任务里，在社交网络预测、金融网络反欺诈等任务中对子图进行计数都是一个很有意义的能力。

5. GNN对子图计数的能力有限

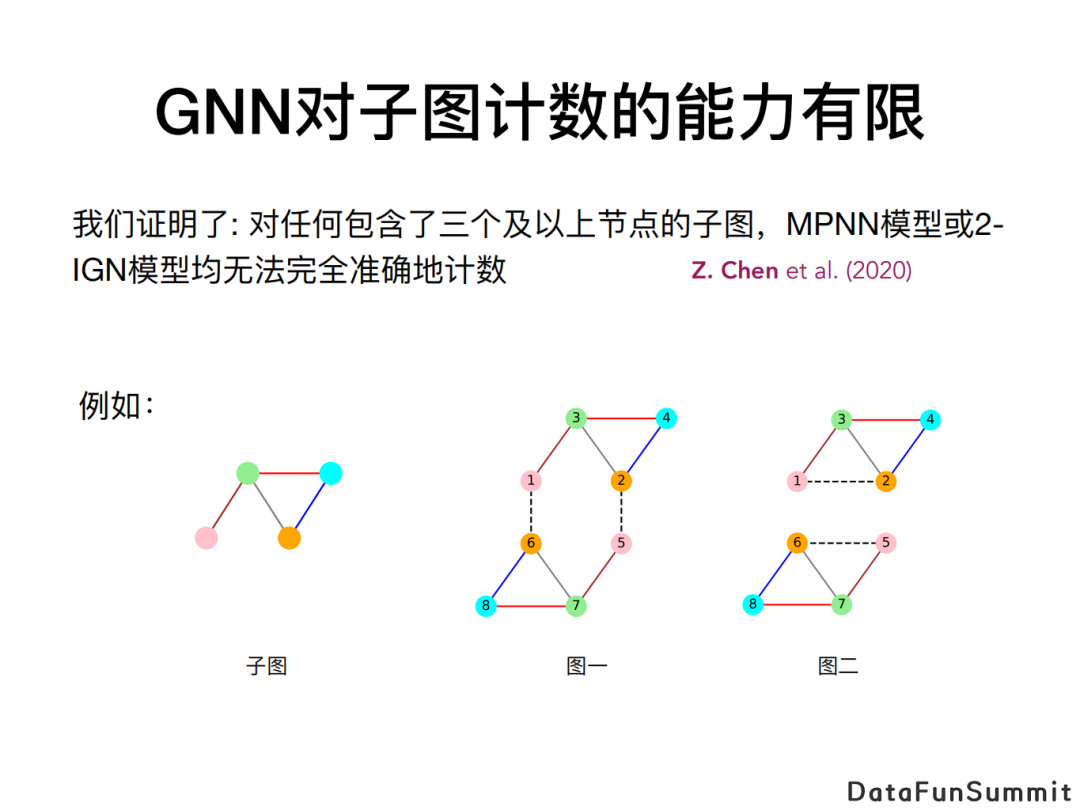
我们证明了传统的GNN模型，包括MPNN和刚才所提的2-IGN模型，即便在理论上也无法做到完全准确地对子图进行计数。

如上图，假设左边为希望进行计数的范型(pattern)。观察图一和图二，我们想数一数两个图里分别有多少个induced subgraph和该范型同构。可以发现，图一含有两个和该范型同构的induced subgraph; 而图二虽然有两个sub graph与该范型同构，但它没有一个induced subgraph和该范型同构。然而同时，我们可以证明MPNN和2-IGN都没有办法区分图一和图二，即不存在一个MPNN或2-IGN可以在图一和图二上给出不同的输出。因此，我们说MPNN和2-IGN无法对此范型进行计数。

6. 构造能对子图计数的模型

基于上述想法，我们提出了一个能对子图进行计数的更具表达能力的模型。假如我们感兴趣的子图较小，那它们会出现在较小的局部邻域(local neighborhood)里，此时只需对每个局部邻域打造具有表达能力的模型，然后再聚合所有局部邻域上的模型输出就可以获得子图数量的全部信息了。

我们这里对每个局部邻域用到的具有表达能力的模型叫作Relation Pooling(RP)。其基本想法是，若想得到一个满足置换不变性(permutation-invariance)的函数的话，我们可以通过对不满足置换不变性的函数进行symmetrization，比如通过枚举所有种置换然后对函数输出进行加和或取平均。这样的一个模型表达能力很强，但计算复杂度较高，如果输入图的大小是N的话，计算复杂度为N的阶乘。

而我们的想法是把RP模型用到每一个局部邻域上，再把所有局部邻域上得到的输出进行合并。设感兴趣的子图的半径是R的话，此时总计算复杂度为N乘以R的阶乘。如果R较小但N很大，计算复杂度远小于N的阶乘。这就是我们的Local Relational Pooling (LRP)模型。LRP模型也可被迭代式的应用，这时候可得深层的Deep LRP模型。

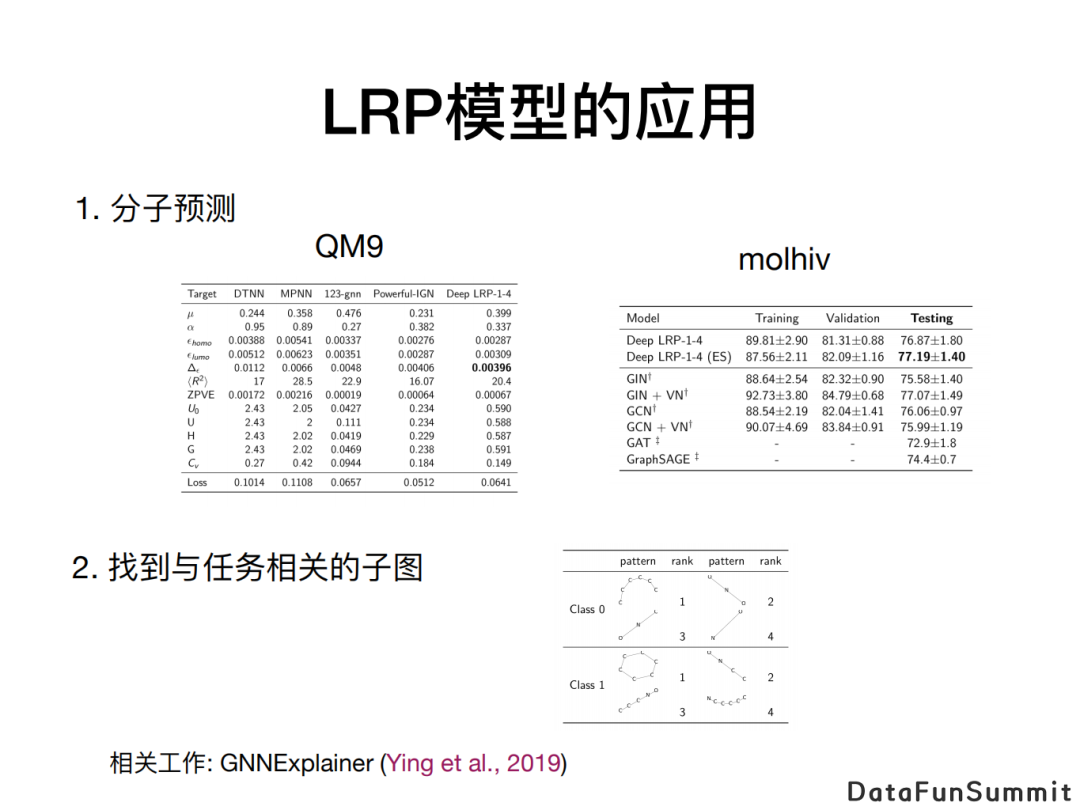
7. LRP模型的应用

我们把LRP模型应用到分子预测的任务上，如QM9和molhiv数据集，实验结果理想。此外，我们一方面可以通过LRP模型来预测分子性质，另一方面也可以用它来寻找与某个分子性质相关的子图，比如发现哪个官能团与分子的毒性或者是水溶性关联密切，以此达到解释的目的。

Graph-Augmented MLP

1. “GNN简化版“：Graph-Augmented MLP

最后一个话题，我们考虑一类简化版的GNN，称为Graph-Augmented MLP (GA-MLP)。它基本的想法是把对节点特征的变换(transformation)和传播(propagation)分开。相比于MPNN，此类模型用一些多跳的图算子来生成额外的节点特征（augmented nodefeature），从而利用到长距离的信息，而非通过多层的消息传播来得到。作为简化版的GNN，它一方面有更好的可扩增性(scalability)，可被应用到较大的图上，另外也可能缓解过平滑化(over-smoothing)的问题。

我们这里感兴趣的是，在这些优点之外，Graph-Augmented MLP相对于GNN是否在表达能力上有所欠缺。

2. GNN vs Graph-Augmented MLP

我们首先比较它们区分非同构图能力的差异。我们发现，确实能找到一些说明差异的例子，比如上图不能被只使用邻接矩阵的幂(powers of the adjacency matrix)的Graph-Augmented MLP来区分，但可被GNN区分。不过，这个结果在直观上并不能告诉我们有哪些任务是Graph-Augmented MLP所不擅长的。

对此，我们提出新的衡量标准，即考虑模型能否对图上带特征的游走(attributed walks)进行计数。大概想法是：我们想数一数由某个节点出发，能找到多少条满足特征要求的游走。比如，如果我们用不同颜色来代表节点的不同特征，我们想数一数有多少条游走满足“第一跳是红色节点，第二跳绿色节点，第三跳是蓝色节点”这样一个要求。

对于上述计数任务，我们可以证明Graph-Augmented MLP是做不到的，而MPNN理论上可以做到。因为GNN有能力获取rooted subtree的信息，这些信息里就包含了所有的游走，然而Graph-Augmented MLP无法完全保留这些信息。我们进行一些实验，也支持了这个结论。

3. 不同算子的区别

此外，Graph-Augmented MLP还受其所用的算子集合优劣性的限制。

我们在社群发现(community detection)任务上对比GNN和两种Graph-Augmented MLP。其中一种Graph-Augmented MLP是基于邻接矩阵的幂，另外一种是基于最优Bethe Hessian矩阵的幂。我们发现使用最优Bethe Hessian矩阵得到的结果优于使用邻接矩阵，并与GNN的结果相近。这也是Graph-Augmented MLP一类模型的性质，模型效果取决于是否找到好的算子。

然而，对最优Bethe Hessian矩阵本身的计算是依赖于图数据的而非先验。相比之下，GNN则有能力通过数据来直接学习合适的消息传播方式。不过更一般性的一些结论还需要进一步研究。

总结

我们讨论了三个衡量GNN表达能力的标准：

能否对非同构图进行区分；
能否对子图进计数；
能否对带特征的游走进行计数。

其中后两个衡量标准，是我们认为对一些实际应用较相关且可直观理解的标准。基于上述标准，我们证明了一些已有模型在表达能力上的局限，并根据理论结果提出了更具有表达能力模型，包括Ring-GNN以及Local Relational Pooling，它们在分子预测及寻找更适合任务的子图等实验有很不错的表现。

精彩问答

Q：表达能力是不是和模型实际应用的效果成正比，有应用的例子对比吗？

A：表达能力只是一方面，模型还有很多别的方面要考虑，如优化，泛化以及稳定度，可扩增性等。并不是表达能力更强的模型一定就有更好的表现，模型表现是和任务有关的。我们一般的经验是，在分子预测的情境下，强表达能力模型常常有更好的表现。因为分子图较小，模型可扩增性不是瓶颈，我们希望通过让模型变得更复杂的方式来获得更强的表达能力。但在其他的场景，如社交网络等大图，可扩增性和过平滑化等现象可能也需要关注。而且用复杂的模型可能导致过拟合，反而被噪声干扰。

Q：MPNN也是根据邻接矩阵进行聚合和传播的，这和Graph-Augmented MLP类型工作的本质区别在哪里?

A：在MPNN中, 信息在图中传播的距离和神经网络的深度是一致的，比如用十层的MPNN，那节点就能获得十跳之外的节点信息；相比之下，可以说Graph-Augmented MLP是一种“浅”的神经网络，若想获得十跳以内的信息，我们不做十层的信息传播，而是用十跳的图算子，比如说邻接矩阵的十次方，来生成augmented node feature，之后对每个节点分别使用两层或三层的MLP就可以了。

Q：讲座中提到Graph-Augmented MLP的表达能力比GNN弱，是没有像GNN一样交替地做propagation，transformation造成的吗？

A：我觉得可以理解成这个原因。以下图两个不同的rooted subtree为例。

一个两层的MPNN可以完全获得图中rooted subtree的信息并区分它们。因为在MPNN做第一层消息传播后，节点2处得到的嵌入向量就有区别了，然后再通过第二层消息传播将信息传回根节点。

然而Graph-Augmented MLP模型，以使用邻接矩阵的幂作为图算子集的情况为例，只能让根节点知道每层的子节点里绿色的节点和蓝色节点数量，而无法得到更具体信息，因此无法区分上面两个rooted subtree。

Q：如上个问题所讨论的图例，是否能理解为GNN有保序的能力而Graph-Augmented MLP所学信息是无序的？

A：也并不完全说。就像刚才所说，GNN可以获取完整的rooted subtree信息，但Graph-Augmented MLP所收集的信息更像是对每层子节点特征的整体上的统计信息。直观上是这样理解，我觉得关于序的问题欢迎进一步的探讨。

Q：为什么衡量模型的表达能力和子图计数相关？

A：这是我们所提出的一个衡量表达能力的标准。根本上，衡量GNN表达能力的标准是对图上函数的逼近的能力，即universal approximation的问题：是不是对一个图上的任意函数，都可以用GNN来逼近。这与对前馈神经网络表达能力的研究比较类似。从这根本观点出发，我们思考什么样的函数是GNN能够表达的。具体的，我们尝试探究与现实任务有所关系的函数，如研究GNN能不能逼近子图计数这一类函数。

今天的分享就到这里，谢谢大家。

在文末分享、点赞、在看，给个3连击呗~

分享嘉宾：