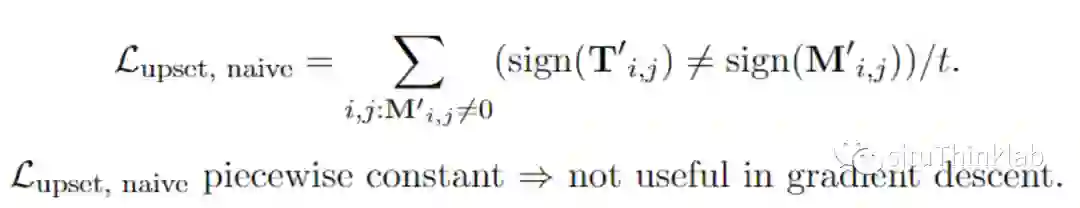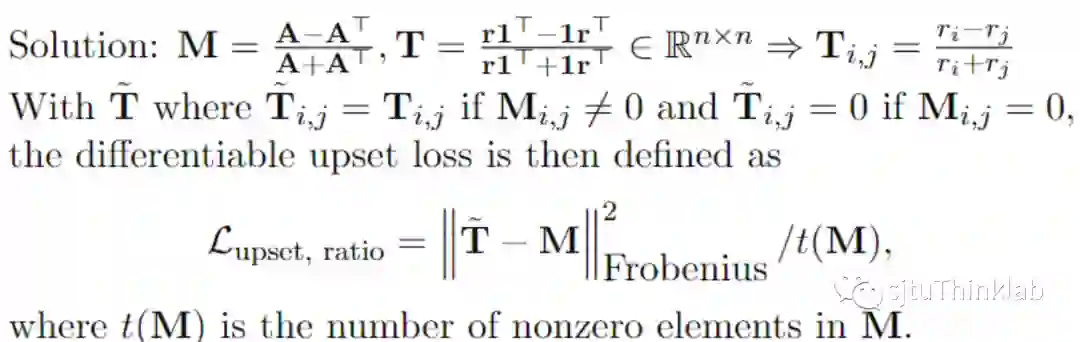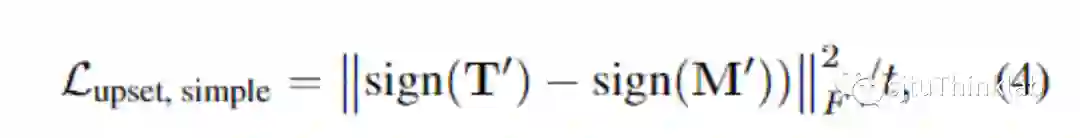【ICML2022】GNNRank: 基于有向图神经网络从两两比较中学习全局排序

2022 年 7 月 25 日 专知

本文简要介绍由牛津大学博士生何奕萱在上海交通大学访问期间与交大及亚马逊人工智能实验室合作发表的一篇ICML 2022论文 GNNRank: Learning Global Rankings from Pairwise Comparisons via Directed Graph Neural Networks，旨在推动机器学习求解图论与组合问题。

作者：何奕萱，甘全，David Wipf, Gesine Reinert, 严骏驰，Mihai Cucuringu

论文链接：https://proceedings.mlr.press/v162/he22b/he22b.pdf（可点击阅读原文查看）

代码链接：https://github.com/SherylHYX/GNNRank

摘要：

从两两的比较中恢复全局排名具有广泛应用。与比赛中的比赛相对应的成对比较可以解释为有向图（有向图）中的边，其节点表示例如排名未知的竞争对手。在本文中，我们通过提出所谓的 GNNRank 将神经网络引入排序恢复问题，这是一种可训练的基于图神经网络的有向图嵌入框架。此外，我们设计了新的目标来编码排名混乱/违规。该框架涉及排名分数估计方法，并通过展开由可学习的相似性矩阵构造的图的 Fiedler 向量计算来添加归纳偏差。大量数据集的实验结果表明，我们的方法相对于基线获得了具有竞争力且通常更出色的性能，并显示出不错的迁移能力。

动机

从反映相对潜在优势或分数的成对比较中恢复全局排名是信息检索中的一个基本问题。在分析大规模数据集时，人们通常会寻求各种形式的数据排序（即排序），以识别最重要的条目、有效计算搜索和排序操作或提取主要特征。这个问题的应用很广，包括亚马逊的 Mechanical Turk 众包系统、Netflix提供的电影推荐系统以及足球比赛等的排名等都需要用到两两的排名比较信息来得到全局的排名。然而，解决排名估计问题的现有方法迄今尚未利用强大的神经网络架构来优化排名目标。因此，我们用神经网络增强了某种排序算法，特别是图神经网络 (GNN)，因为它与手头问题的内在联系。

问题定义

不失一般性，我们考虑比赛中的成对比较，这些比较可以在有向图（有向图）𝐺=（𝑉，𝐸）中进行编码。

节点集𝑉：竞争对手。
边集𝐸：成对比较。
邻接矩阵：匹配的结果。

从成对比较中恢复全局排名相当于为每个节点 𝑣_𝑖∈𝑉 分配一个整数 𝑅_𝑖，表示其在竞争者中的位置，其中排名越低，节点越强。我们的办法是，首先尝试为所有节点学习技能级别向量𝑟，其中较高的技能值对应于较低的等级排序。

SerialRank[1]

首先计算某个相似度矩阵𝑺'的拉普拉斯算子。

在全局符号协调之后，𝑺'对应的 Fiedler 向量用作最终排名估计。

虽然在实践中通常有效，但 SerialRank 的表现重度取决于相似度矩阵 𝑺' 的质量。

为了解决这个问题，我们引入了一个参数化的 GNN 模型，它允许我们计算可训练的相似性度量，这对后续排名很有用。

方法

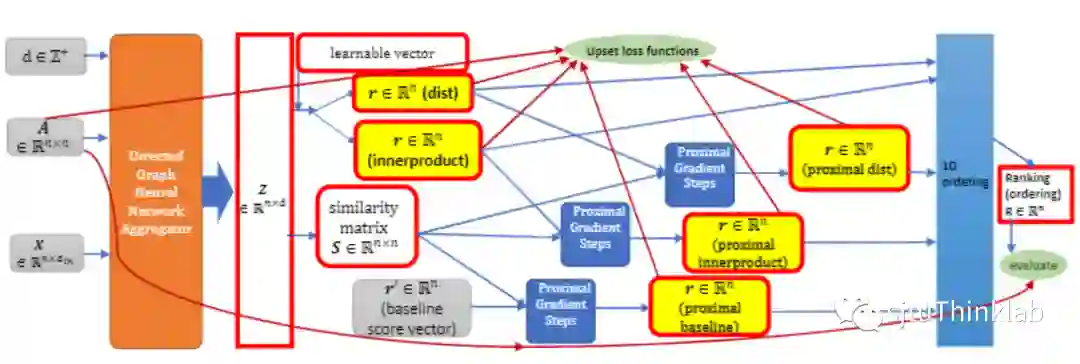
图为我们的 GNNRank 框架：从成对比较矩阵 A 和一些节点特征矩阵 X 开始，我们首先应用有向图神经网络聚合器来获得节点嵌入矩阵 Z。然后可以基于 Z 构造可学习的相似度矩阵 S。“dist”和“innerproduct”是从 Z 矩阵派生的两个非近端变体，不涉及近端梯度步骤。对于展开可学习相似度矩阵 S 的 Fiedler 向量计算的近端变体，需要初始猜测，这可能是非近端变体的输出之一，或基线方法的输出 r'。然后可以将损失函数应用于技能级别向量 r，并且可以通过对 r 向量进行排序来获得最终排名R向量。最后，我们可以评估我们的结果。

获取节点嵌入可以应用任何能够考虑方向性和输出节点嵌入的 GNN 方法。例如，DIMPA [2]、DiGCN [3]。我们记最终节点嵌入为 𝒁∈ℝ^(𝑛×𝑑)，节点 𝑣_𝑖 的嵌入向量 𝑧_𝑖 是 𝒛_𝑖≔(𝒁)_((𝑖,:))∈ℝ^𝑑，𝑖的第i行。

为了获得最终的排名分数，我们用近端梯度步骤展开了由我们的对称相似矩阵𝑺构造的图的 Fiedler 向量的计算。从高维嵌入矩阵𝒁，我们计算对称相似矩阵𝑺，其中𝑆_(𝑖,𝑗)=exp(−|𝑧_𝑗−𝑧_𝑖|^2/(𝜎^2 𝑑))。然后，我们应用近端梯度步骤来逼近 𝑺 的 Fiedler 向量，该向量用作技能级别向量 𝒓。

损失函数以及评价指标

评价指标除了upset naïve的指标之外还有一个可以区分 0 vs 1跟 -1 vs 1的：

此外，如果有真实的排名，我们可以用Kendall Tau [4] 数据来评价。

数据集

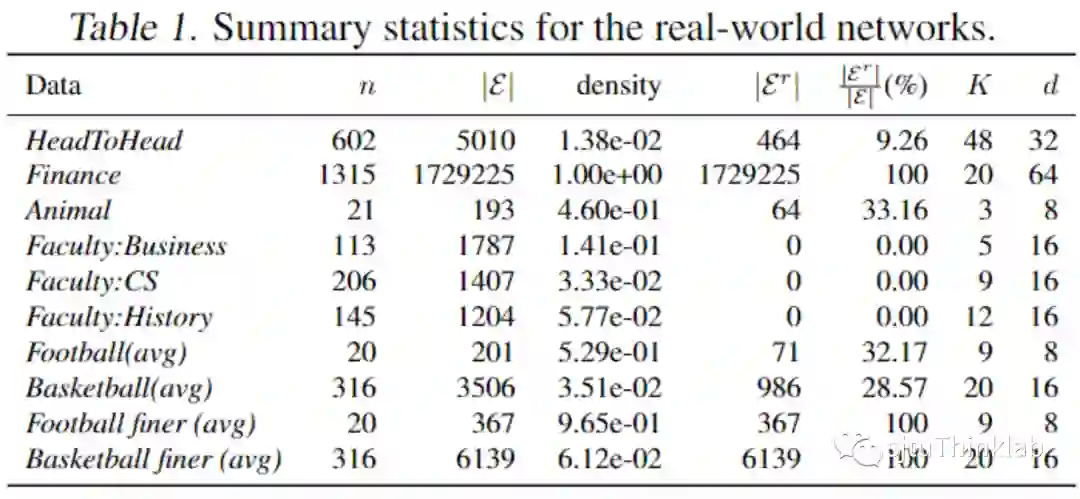
我们考虑了 10 个真实世界的数据集（总共构建了 78 个有向图）。在大多数情况下，基于成对比较的有向图构造如下：对于每次比赛，如果比赛结果不是平局，则添加一条边，权重为两端节点比赛中获得分数之间的差异（获胜分数的绝对差异），这种情况下平局跟没有比赛是没有区别的。

当两个竞争对手的个人比赛得分的原始数据可以被获取时，我们另外构建一个更细颗粒度的版本（记号为“finer”），该版本将平局考虑在内，如下所示：对于每场比赛，我们添加一条也许是两个方向权重不都为零的边，而且权重很可能是不一样的。如果有多场比赛，我们会对权重进行求和。为了区分零（平局）和没有比赛，在我们的数据处理中，我们对于每一场比赛的每一个分数都添加一个小值（此处为 0.1）。实际数据的总结表格如表1所示。表1给出节点数n、有向边数|E|、双向边边数 |E^r|（自循环的边计算一次，而对于两个不同的节点之间的一条边，双向边计算两次）及其在所有边中的百分比。此外我们罗列了网络大小的方差和密度（定义为 |E|}/[n(n-1)]）。

当输入特征没有被提供时，我们按照[2]中的办法生成特征，堆叠 (A-A^T) · i 的最大 K个特征向量的实部和虚部用于 GNN的输入特征。此外我们报告通过有向图GNN生成的节点嵌入的维度d。

除了真实世界的数据集之外，我们还做了生成数据的数据集。我们对 E R Outlier (ERO) 模型， n=350个节点的图进行实验, 数据集具体信息参考[5]，边密度p为 0.05或1，噪声水平eta从0到0.8以0.1为步长进行变化，并且沿用样式“uniform”或“gamma”对于生成真实分数的分布。我们为这些ERO 模型固定 K=5, d=16。

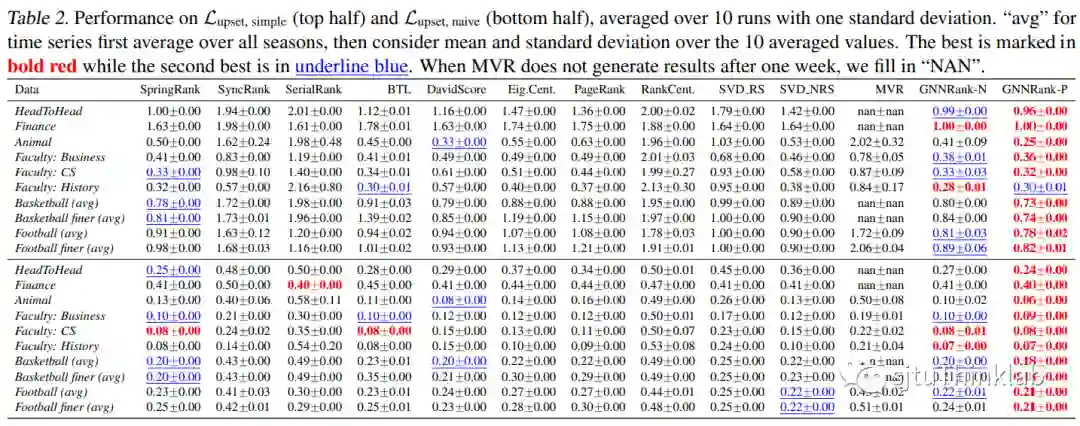
主要实验结果

对于一些密集的合成有向图，SerialRank（它激发了我们的近端梯度步骤）获得了领先的性能，而在其他一些情况下它失败了。我们在所有数据集中观察到我们的近似方法：1）通常优于非近端变体；2）当使用它们作为初始猜测时，可以改进现有的基线方法，并且永远不会比相应的基线表现更差，因此它们可以用来增强现有的方法；3）不要依赖基线方法进行初始猜测，而是可以使用非近端结果；4）可以通过使用可训练的相似度矩阵和近端梯度步骤展开其 Fiedler 向量计算来超越 SerialRank的表现。

全文总结

图论与组合问题的机器学习求解具有广阔的研究空间和应用价值，本文所提出的方法本质上是一个基于GNN的unrolling框架，对传统求解全局排序的Serialrank算法进行神经网络的二次实现，并对其收敛性质给出了相关理论分析。实验结果展示我们的方法具有良好的拟合能力和泛化能力。

参考文献

[1] Fogel, F., d'Aspremont, A., & Vojnovic, M. (2014). Serialrank: Spectral ranking using seriation. Advances in Neural Information Processing Systems, 27.

[2] He, Y., Reinert, G., & Cucuringu, M. (2021). DIGRAC: Digraph Clustering Based on Flow Imbalance. arXiv preprint arXiv:2106.05194.

[3] Tong, Z., Liang, Y., Sun, C., Li, X., Rosenblum, D., & Lim, A. (2020). Digraph inception convolutional networks. Advances in neural information processing systems, 33, 17907-17918.

[4] Brandenburg, F. J., Gleißner, A., & Hofmeier, A. (2013). Comparing and aggregating partial orders with kendall tau distances. Discrete Mathematics, Algorithms and Applications, 5(02), 1360003.

[5] d'Aspremont, A., Cucuringu, M., & Tyagi, H. (2021). Ranking and synchronization from pairwise measurements via SVD. Journal of Machine Learning Research, 22(19).

专知便捷查看