ICML2022|谱图神经网络有多强大？线性GNN就能达到SOTA

标题: ICML2022|谱图神经网络有多强大？线性GNN就能达到SOTA

Paper title: How Powerful are Spectral Graph Neural Networks

Paper link: https://arxiv.org/abs/2205.11172v2

Code: https://github.com/GraphPKU/JacobiConv

Publication Venue: ICML 2022

Institution: Peking University, Beijing Institute for General Artificial Intelligence

Authers: Xiyuan Wang, Muhan Zhang

概述

什么是谱图神经网络

谱图神经网络是一种基于图信号滤波器的图神经网络(GNN)，广泛应用于结点任务。大量知名的GNN可以归入谱GNN，比如ChebyNet[1], GCN[2], BernNet[3]。

给定一个图，令 为其邻接矩阵， 为一个对角元是结点度数的对角矩阵。归一化的拉普拉斯矩阵为 。图信号的多项式滤波器可以表示为 的多项式 。

现有的谱GNN可以归纳为以下形式：

首先使用多层感知机（MLP） 变换图的结点特征 ，然后使用多项式滤波器对特征滤波，最后用另一个MLP 变换滤波后特征。通过设计/学习多项式系数，谱GNN可以模拟各种滤波器（低通、带通、高通），可以处理同质图和异质图。

我们的工作

我们研究简化的谱GNN：线性GNN

首先使用线性变换变换结点特征 ，然后对特征滤波得到输出。线性GNN的价值有三个方面1. 给出了谱GNN表示能力的下界。2. 由于其可扩展性高，有广泛的应用 3. 我们发现线性GNN在理论上的表示能力足够强，在实验中的表现也显著高于有非线性函数的GNN。

尽管已经出现了大量的谱GNN模型，但谱GNN的表示能力仍然没有得到充分研究。此外，这些模型的主要区别在于构建滤波器函数的基函数，但是没有对这些基的性能的系统分析。我们在理论上讨论了这两个问题，得出结论1. 对结点分类任务，在温和条件下，线性GNN可以万能逼近 2. 可以使用正交基来加速模型的优化。据此我们提出了新的谱GNN模型JacobiConv，其架构非常简单，没有非线性函数。但是JacobiConv在实验中超过了现有的方法，由此验证了我们的理论。

理论分析

谱图神经网络的表示能力

主定理:

如果 没有多重特征值并且结点特征 包含所有频率分量，则线性GNN可以产生任何一维预测。

由此可以得到线性GNN表示能力的三大瓶颈。

1. 多维输出。瓶颈在于线性GNN为每一个输出维度使用相同滤波器。为每个维度使用不同滤波器可以完全解决这一问题。
2. 的多重特征值。多重特征值指矩阵有多个线性无关的特征向量有相同的特征值，相当于多个频率分量有相同的频率。这导致滤波器不能对信号中的同频不同分量进行不同过滤。我们发现多重特征值与高对称性密切相关，而真实图的对称性低。在我们的10个真实数据集上，仅有不到1%的特征值是多重的。
3. 结点特征 缺失一些频率分量。这导致线性GNN的输出也会缺失相应的分量。真实图的结点特征往往非常丰富。在我们的10个真实数据集上，没有缺失的频率分量。

由此，对结点问题，在没有多重特征值和缺失频率分量的温和条件下，线性GNN的表示能力已经达到最强。

我们还探究了从滤波器角度分析的表示能力与从图同构角度分析的表示能力之间的联系。我们也分析了非线性函数在GNN中的作用，发现它能混合不同频率的信号。

基选择影响谱图神经网络的优化

可以使用不同的多项式基线性组合得到多项式滤波函数。只要基是完备的，使用不同基的模型的表示能力没有任何区别，但是实验中却发现基的选择对性能有重要影响。

在一定的假设下，我们证明：（以图信号在频域中的强度为权函数的）正交归一多项式作为基 损失函数的Hessian矩阵条件数最低 优化最快。

由此，我们分析了过去各种模型使用的基的优劣，并引入Jacobi多项式。它是一类多项式，可以变化形式以适应数据，在理论上优于现有模型使用的基。Jacobi多项式的具体形式见模型实现。

模型实现

我们的模型称为JacobiConv

1. 使用一个线性层变换结点特征

2. 用 Jacobi基进行滤波

For ,

3. 对滤波后的特征进行 线性组合，得到输出

4. 观察到系数 随基阶数增大而快速衰减，因此将其分解。称为**多项式系数分解(PCD)**技术

其中 是衰减因子。我们设 。

实验

合成数据集

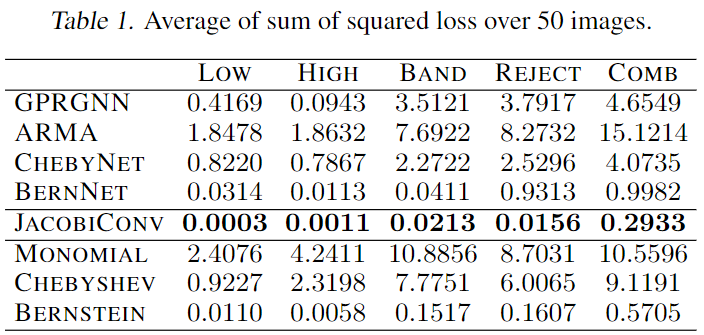
将图片转为图，每个结点是一个像素，特征是像素值。每个结点与4个临近像素结点相连。设计滤波器处理特征。模型输入特征拟合滤波后的特征。结果见表，loss越低性能越高。

模型优于现有的谱GNN（表上半部分），也优于使用其它基的线性GNN（表下半部分）。

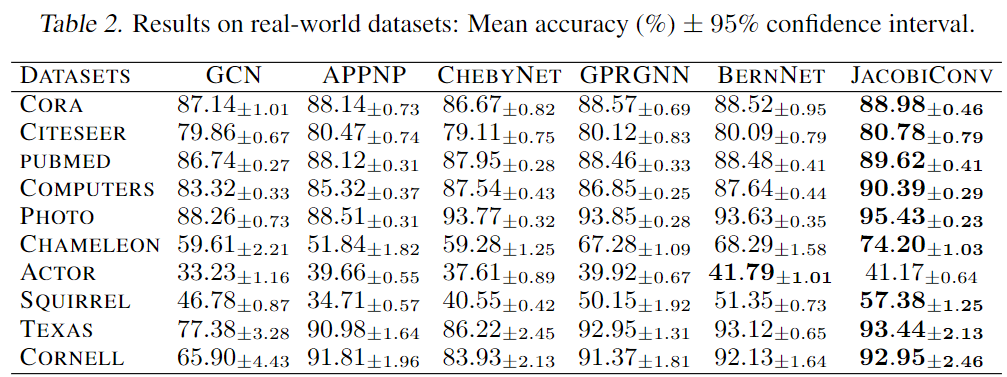
在真实数据集上分类结点

超过现有模型

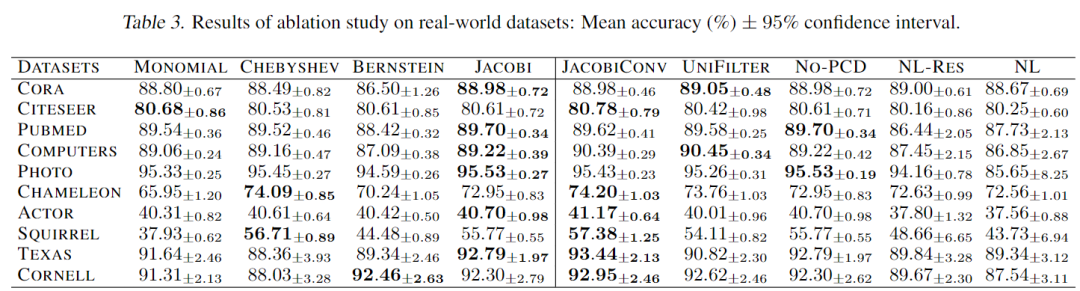
切割分析

Table 3

左侧说明Jacobi基优于其它基函数。右侧说明我们的各种设计都有效：为每个输出维度使用独立的filter，多项式系数分解，去除非线性函数。

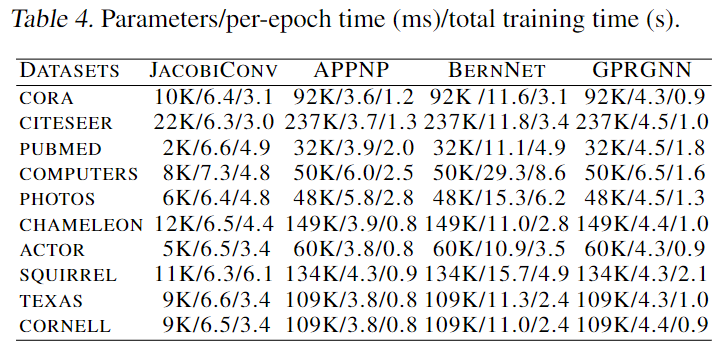
效率

Table 4

仅使用10%参数。训练时间接近。

总结

我们在理论上分析了线性GNN的表示能力与多项式基对谱GNN的影响，得出结论1. 对结点分类任务，在温和条件下，线性GNN可以万能逼近 

2. 可以使用正交基来加速模型的优化。我们提出的JacobiConv模型有着极为简单的架构，并且没有非线性函数。但其精度超过了现有的谱GNN模型，验证了我们的理论。

参考文献

[1] Defferrard, M., Bresson, X., and Vandergheynst, P. Convolutional neural networks on graphs with fast localized spectral filtering. NeurIPS 2016.

[2] Kipf, T. N. and Welling, M. Semi-supervised classification with graph convolutional networks. ICLR 2017.

[3] He, M., Wei, Z., Huang, Z., and Xu, H. Bernnet: Learning arbitrary graph spectral filters via bernstein approximation. NeurIPS 2021.