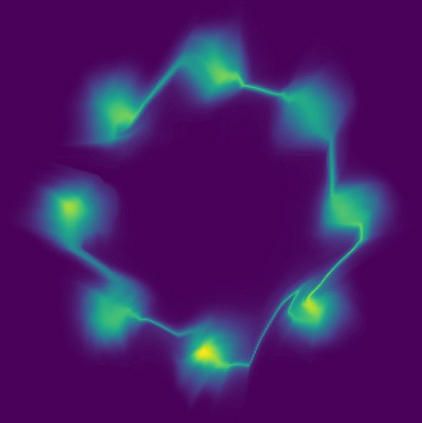
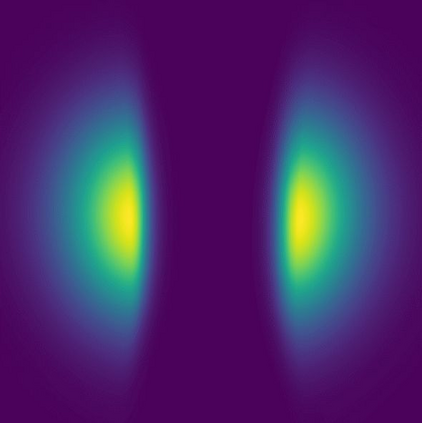
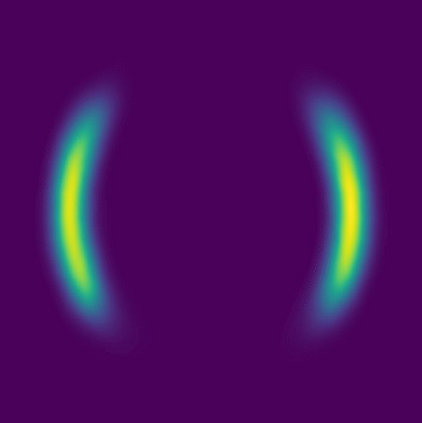
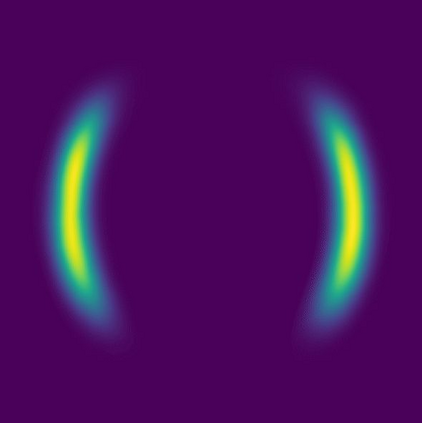
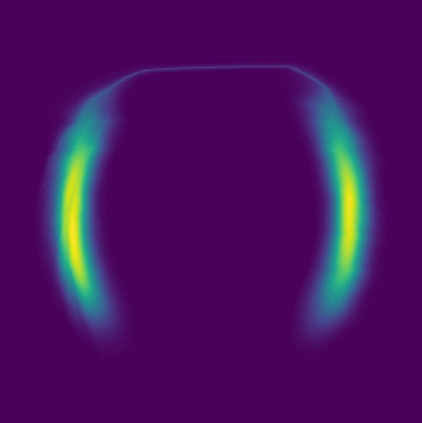
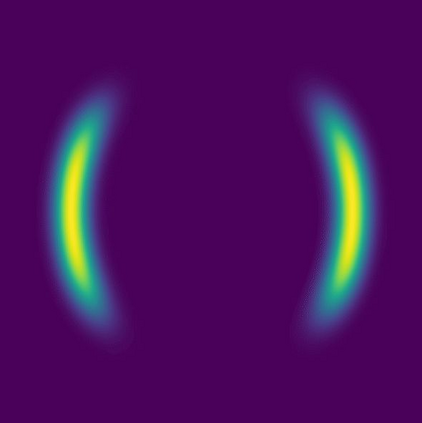
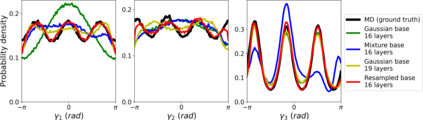
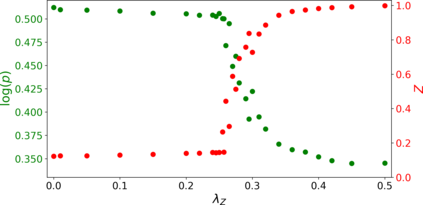
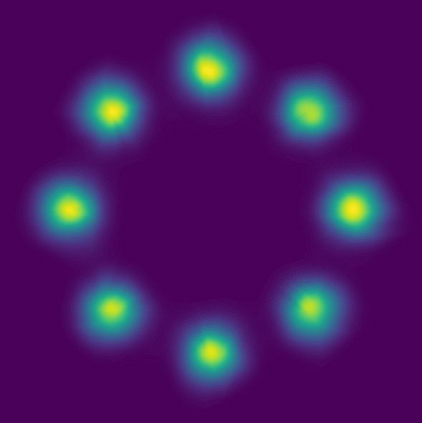
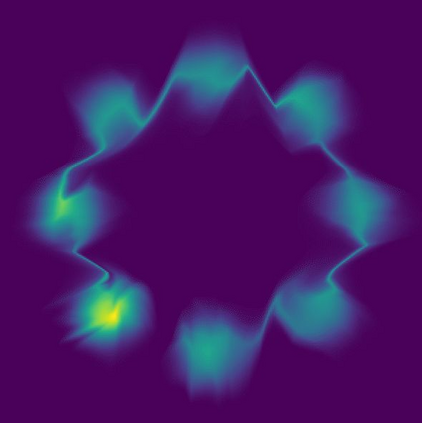
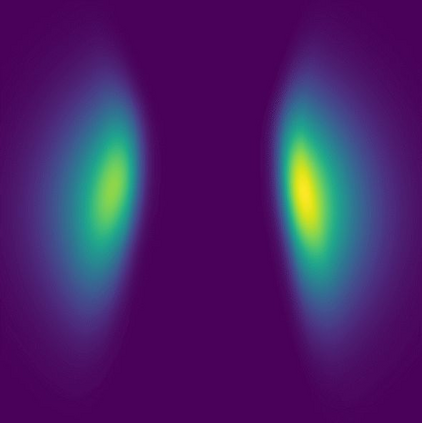
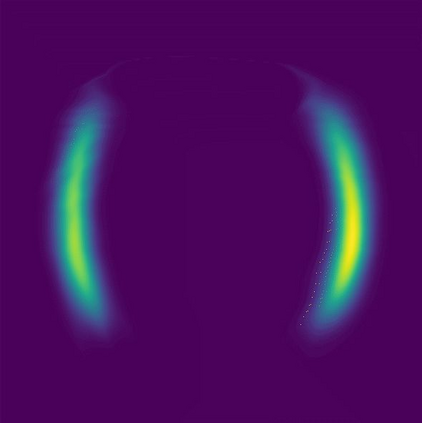
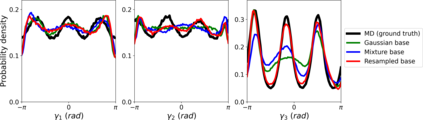
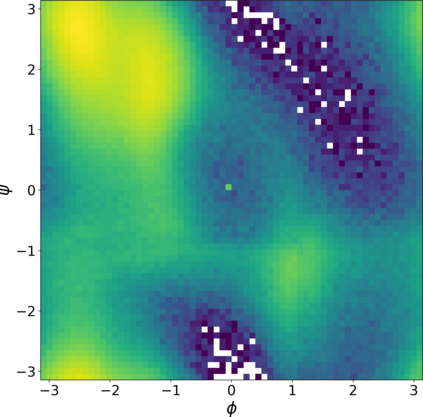
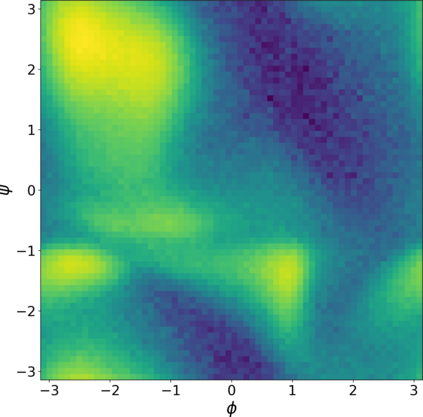
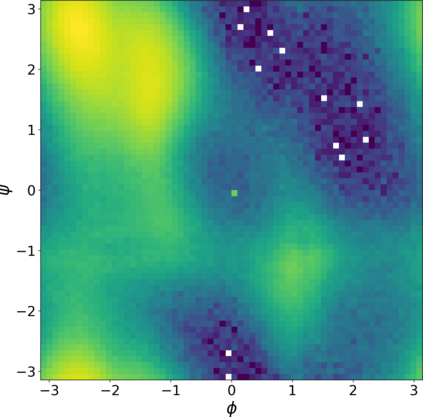
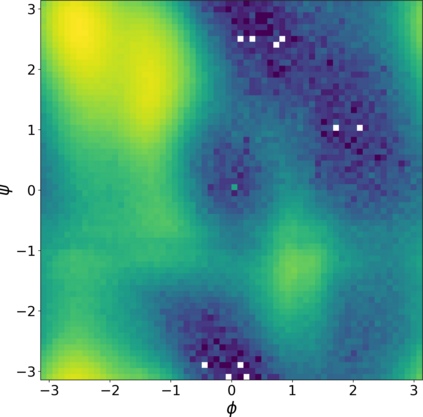
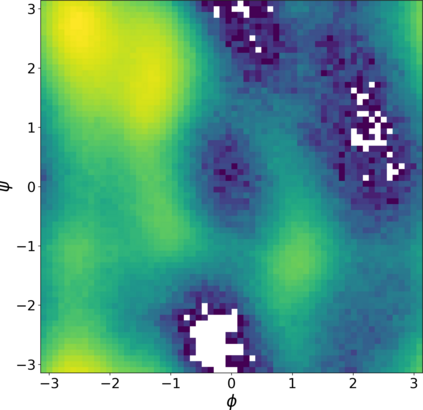
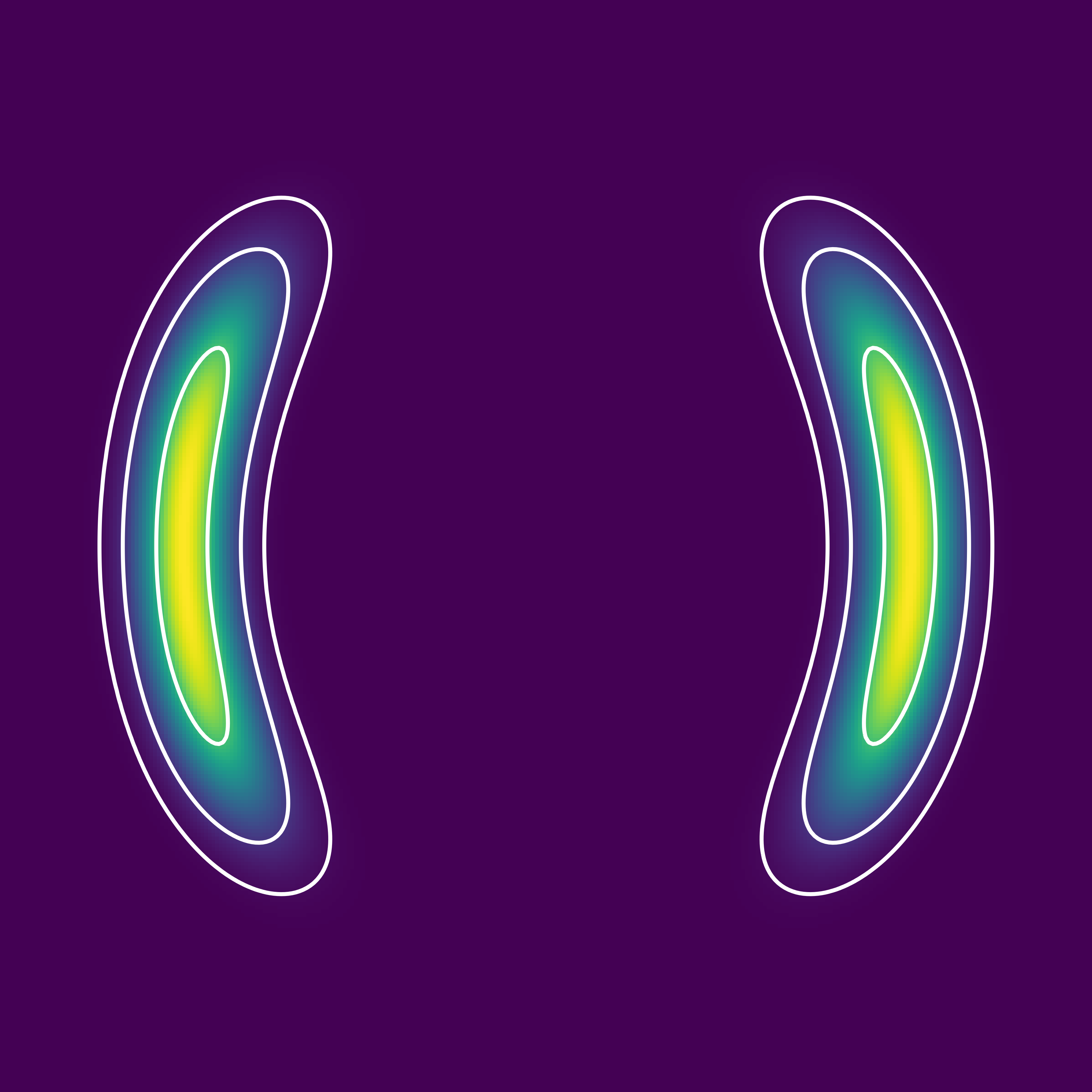
Normalizing flows are a popular class of models for approximating probability distributions. However, their invertible nature limits their ability to model target distributions whose support have a complex topological structure, such as Boltzmann distributions. Several procedures have been proposed to solve this problem but many of them sacrifice invertibility and, thereby, tractability of the log-likelihood as well as other desirable properties. To address these limitations, we introduce a base distribution for normalizing flows based on learned rejection sampling, allowing the resulting normalizing flow to model complicated distributions without giving up bijectivity. Furthermore, we develop suitable learning algorithms using both maximizing the log-likelihood and the optimization of the Kullback-Leibler divergence, and apply them to various sample problems, i.e. approximating 2D densities, density estimation of tabular data, image generation, and modeling Boltzmann distributions. In these experiments our method is competitive with or outperforms the baselines.
翻译:流的正常化是接近概率分布的流行模型类别。 但是,它们的不可逆性限制了它们模拟目标分布的能力,而目标分布的模型支持具有复杂的地形结构,如波尔茨曼分布。 已经提出了几项程序来解决这个问题,但其中许多程序却牺牲了不可逆性,从而牺牲了日志相似性和其他可取特性的可移动性。 为了解决这些局限性,我们引入了一种基础分布基础,在学习的拒绝抽样基础上实现流的正常化,允许由此而来的向模型复杂分布的正常化流,而不会放弃双向性。 此外,我们开发了适当的学习算法,同时利用了对日志相似性的最大化和对 Kullback- Leiber 差异的优化,并将其应用于各种抽样问题,即接近 2D 密度、 表格数据的密度估计、 图像生成和 Boltzmann 分布模型。 在这些实验中,我们的方法具有竞争力,或者超过了基线。