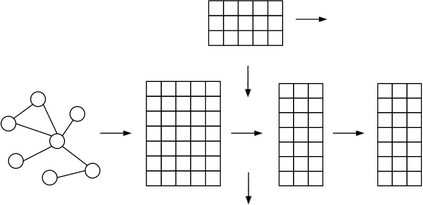
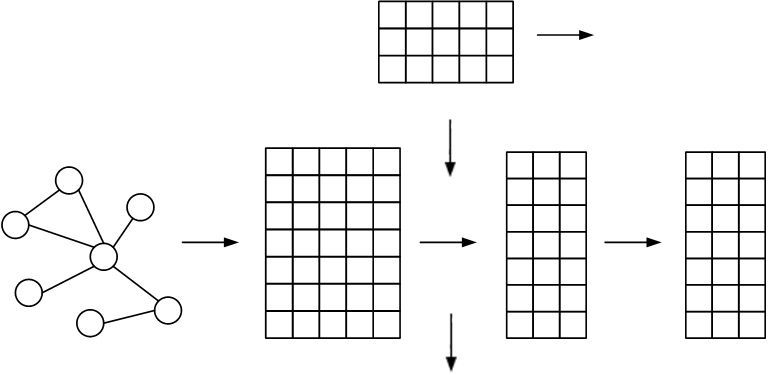
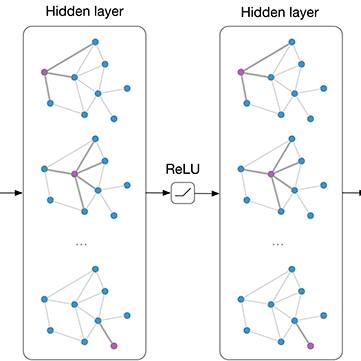
The graph convolution network (GCN) is a widely-used facility to realize graph-based semi-supervised learning, which usually integrates node features and graph topologic information to build learning models. However, as for multi-label learning tasks, the supervision part of GCN simply minimizes the cross-entropy loss between the last layer outputs and the ground-truth label distribution, which tends to lose some useful information such as label correlations, so that prevents from obtaining high performance. In this paper, we pro-pose a novel GCN-based semi-supervised learning approach for multi-label classification, namely ML-GCN. ML-GCN first uses a GCN to embed the node features and graph topologic information. Then, it randomly generates a label matrix, where each row (i.e., label vector) represents a kind of labels. The dimension of the label vector is the same as that of the node vector before the last convolution operation of GCN. That is, all labels and nodes are embedded in a uniform vector space. Finally, during the ML-GCN model training, label vectors and node vectors are concatenated to serve as the inputs of the relaxed skip-gram model to detect the node-label correlation as well as the label-label correlation. Experimental results on several graph classification datasets show that the proposed ML-GCN outperforms four state-of-the-art methods.
翻译:图形共变网络(GCN)是一个广泛用来实现基于图形的半监督学习的工具,它通常将节点特征和图形模拟信息整合在一起,以建立学习模型。然而,对于多标签学习任务,GCN的监督部分只是将最后一个层输出和地面图象标签分布之间的交叉物种流失最小化,这往往会丢失一些有用的信息,如标签相关性等,从而无法取得高性能。在本文件中,我们为多标签分类(即ML-GCN.ML-GCN.ML-GCN首先使用GCN来嵌入节点特征和图示图示图解信息。随后,GCN的监督部分会随机生成一个标签矩阵,其中每行(即标签矢量)代表一种标签。标签矢量的尺寸与GCN上一次变异操作前的节点矢量矢量矢量矢量矩阵的尺寸相同。所有标签和节点都嵌在统一的矢量分类空间(即ML-GN.ML-G-G-G-G-G-G-G-C-C-Ceral-commal-commal-commal-commal-commal-commal-commal-comml-comml-comml-dal-comml-dal-destrisml-dal-dal-destrevol-dal-dal-dal-dal-dal-dal-s-dalismlisml)中,作为Sl 的升级的升级的测试,没有检测到制成数个,以制成的制成的制成的标签-dal-dal-dal-dal-dal-dal-dal-dal-dal-dal-dal-dal-dal-dal-dal-dal-dal-dal-dal-dal-dal-dal-dal-dal-dal-dal-dal-dal-dal-dal-dal-dal-dal-dal-dal-dal-dal-dal-dal-dal-dal-dal-dal-dal-dal-dal-dal-dal-