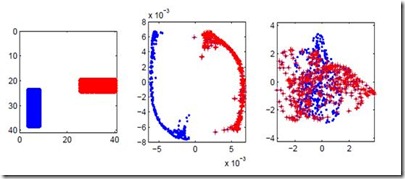
Graph contrastive learning attracts/disperses node representations for similar/dissimilar node pairs under some notion of similarity. It may be combined with a low-dimensional embedding of nodes to preserve intrinsic and structural properties of a graph. In this paper, we extend the celebrated Laplacian Eigenmaps with contrastive learning, and call them COntrastive Laplacian EigenmapS (COLES). Starting from a GAN-inspired contrastive formulation, we show that the Jensen-Shannon divergence underlying many contrastive graph embedding models fails under disjoint positive and negative distributions, which may naturally emerge during sampling in the contrastive setting. In contrast, we demonstrate analytically that COLES essentially minimizes a surrogate of Wasserstein distance, which is known to cope well under disjoint distributions. Moreover, we show that the loss of COLES belongs to the family of so-called block-contrastive losses, previously shown to be superior compared to pair-wise losses typically used by contrastive methods. We show on popular benchmarks/backbones that COLES offers favourable accuracy/scalability compared to DeepWalk, GCN, Graph2Gauss, DGI and GRACE baselines.
翻译:在类似概念下,类似/不同节点的类似/不同节点对相近/不同相异的学习吸引/不同相异的学习节点显示。可以与低维嵌入节点相结合,以保存图的内在和结构特性。在本文中,我们通过对比性学习,推广了著名的拉帕西亚Eigenmaps(Lapalcian Eigenmaps),并将其称为Contrastition Laplecian Eigenmaps(COLES)。从GAN启发的对比性配方开始,我们显示许多对比性图形嵌入模型的詹森-沙农差异在脱节点正和负分布下失败,这些分布在对比性取样期间自然会出现。相比之下,我们从分析上表明,COLES基本上最大限度地减少了瓦列斯特距离的替代点,而众所周知,这种替代点在不协调的分布下可以很好地应对。此外,我们表明COLES的损失属于所谓的块相调损失的家族,先前显示与对比性方法通常使用的配对式损失相比,我们展示了通用的CN基准/后座标/后座,COLES提供了有利的精度、GIGGGGG和GRGV的基线。