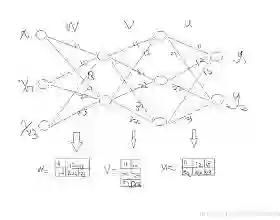
Stochastic gradient descent with backpropagation is the workhorse of artificial neural networks. It has long been recognized that backpropagation fails to be a biologically plausible algorithm. Fundamentally, it is a non-local procedure -- updating one neuron's synaptic weights requires knowledge of synaptic weights or receptive fields of downstream neurons. This limits the use of artificial neural networks as a tool for understanding the biological principles of information processing in the brain. Lillicrap et al. (2016) propose a more biologically plausible "feedback alignment" algorithm that uses random and fixed backpropagation weights, and show promising simulations. In this paper we study the mathematical properties of the feedback alignment procedure by analyzing convergence and alignment for two-layer networks under squared error loss. In the overparameterized setting, we prove that the error converges to zero exponentially fast, and also that regularization is necessary in order for the parameters to become aligned with the random backpropagation weights. Simulations are given that are consistent with this analysis and suggest further generalizations. These results contribute to our understanding of how biologically plausible algorithms might carry out weight learning in a manner different from Hebbian learning, with performance that is comparable with the full non-local backpropagation algorithm.
翻译:神经神经网络的工作马是人工神经网络的工作马。 人们早已认识到, 反向调整不能是一种生物上合理的算法。 从根本上说, 它是一个非本地程序 -- -- 更新一个神经神经元的合成重量要求了解下游神经神经元的突变重量或可接受领域。 这限制了使用人工神经网络作为理解大脑信息处理的生物原则的工具。 Lillicrap et al. (2016) 提出了一种更具有生物上合理性的“ 后退校准” 算法, 该算法使用随机和固定反向调整重量, 并显示有希望的模拟。 在本文中, 我们通过分析两层网络在正方位误差损失下的趋同和校准, 来研究反馈校准程序的数学特性。 在过分分化的环境下, 我们证明错误会趋同为零, 并且为了使参数与随机反向反向调整重量而需要规范。 模拟符合这一分析, 并且建议进一步的概括性分析。 这些结果有助于我们了解反馈程序的数学特性特性, 与他完全的演算法可能以不同的方式学习不同的方式, 。