反向传播 - 专知主题

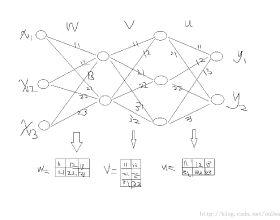
反向传播一词严格来说仅指用于计算梯度的算法，而不是指如何使用梯度。但是该术语通常被宽松地指整个学习算法，包括如何使用梯度，例如通过随机梯度下降。反向传播将增量计算概括为增量规则中的增量规则，该规则是反向传播的单层版本，然后通过自动微分进行广义化，其中反向传播是反向累积（或“反向模式”）的特例。在机器学习中，反向传播（backprop）是一种广泛用于训练前馈神经网络以进行监督学习的算法。对于其他人工神经网络（ANN）都存在反向传播的一般化–一类算法，通常称为“反向传播”。反向传播算法的工作原理是，通过链规则计算损失函数相对于每个权重的梯度，一次计算一层，从最后一层开始向后迭代，以避免链规则中中间项的冗余计算。