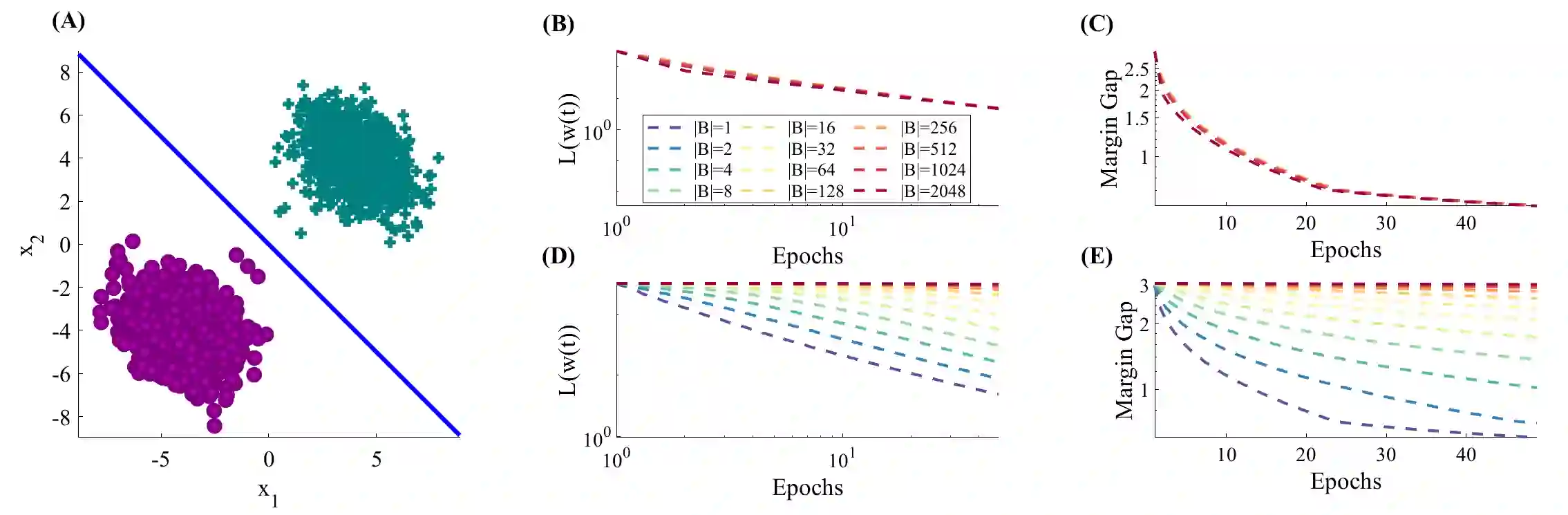
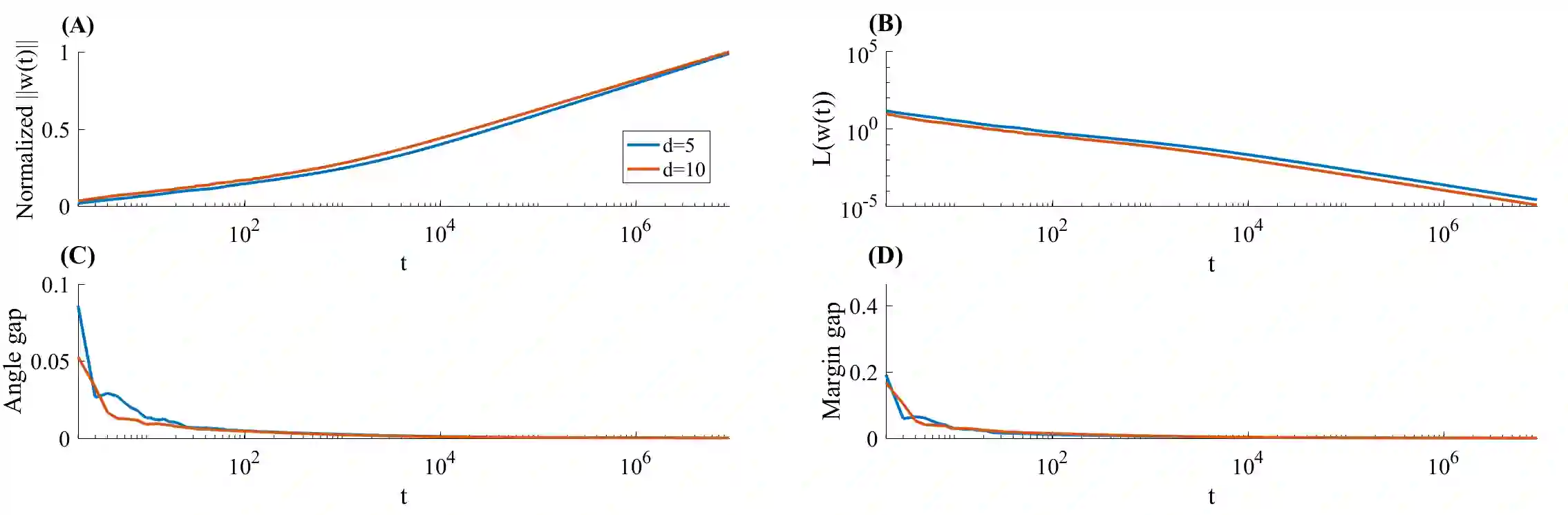
Stochastic Gradient Descent (SGD) is a central tool in machine learning. We prove that SGD converges to zero loss, even with a fixed (non-vanishing) learning rate - in the special case of homogeneous linear classifiers with smooth monotone loss functions, optimized on linearly separable data. Previous works assumed either a vanishing learning rate, iterate averaging, or loss assumptions that do not hold for monotone loss functions used for classification, such as the logistic loss. We prove our result on a fixed dataset, both for sampling with or without replacement. Furthermore, for logistic loss (and similar exponentially-tailed losses), we prove that with SGD the weight vector converges in direction to the $L_2$ max margin vector as $O(1/\log(t))$ for almost all separable datasets, and the loss converges as $O(1/t)$ - similarly to gradient descent. Lastly, we examine the case of a fixed learning rate proportional to the minibatch size. We prove that in this case, the asymptotic convergence rate of SGD (with replacement) does not depend on the minibatch size in terms of epochs, if the support vectors span the data. These results may suggest an explanation to similar behaviors observed in deep networks, when trained with SGD.
翻译:SGD 是机器学习的核心工具。 我们证明, SGD 归结为零损失, 即使是固定的( 非损耗) 学习率, 在单线性线性分类器的特殊情况下, 以线性分解数据优化, 以线性分解数据优化 。 以前的工作假设要么是学习率消失, 循环平均率, 或者是损失假设, 与用于分类的单线性损失函数不相符, 如后勤损失。 我们证明, 无论是抽样还是不替换的固定数据集的结果。 此外, 在后勤损失( 和类似的指数性分解损失) 方面, 我们证明, 在 SGD 中, 重量矢量向方向趋近于$L_ 2美元的最大边矢量为$O( 1/\log( t) ), 而损失则与 $O( 1/ t) 相近, 与梯度下降值相似。 最后, 我们检查一个固定学习率与微型分解大小相称的例子。 此外, 在本案中, 后勤损失( 和类似的超尾量损失), 我们证明, 当SGDGD 网络的迷性趋同性趋同的行为解释时, 时, 可能不取决于SGDM 的精确的精确的粘合率率率, 的SGDB 的计算结果。