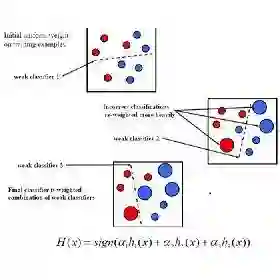
AdaBoost is one of the most popular ML algorithms. It is simple to implement and often found very effective by practitioners, while still being mathematically elegant and theoretically sound. AdaBoost's interesting behavior in practice still puzzles the ML community. We address the algorithm's stability and establish multiple convergence properties of "Optimal AdaBoost," a term coined by Rudin, Daubechies, and Schapire in 2004. We prove, in a reasonably strong computational sense, the almost universal existence of time averages, and with that, the convergence of the classifier itself, its generalization error, and its resulting margins, among many other objects, for fixed data sets under arguably reasonable conditions. Specifically, we frame Optimal AdaBoost as a dynamical system and, employing tools from ergodic theory, prove that, under a condition that Optimal AdaBoost does not have ties for best weak classifier eventually, a condition for which we provide empirical evidence from high dimensional real-world datasets, the algorithm's update behaves like a continuous map. We provide constructive proofs of several arbitrarily accurate approximations of Optimal AdaBoost; prove that they exhibit certain cycling behavior in finite time, and that the resulting dynamical system is ergodic; and establish sufficient conditions for the same to hold for the actual Optimal-AdaBoost update. We believe that our results provide reasonably strong evidence for the affirmative answer to two open conjectures, at least from a broad computational-theory perspective: AdaBoost always cycles and is an ergodic dynamical system. We present empirical evidence that cycles are hard to detect while time averages stabilize quickly. Our results ground future convergence-rate analysis and may help optimize generalization ability and alleviate a practitioner's burden of deciding how long to run the algorithm.
翻译:AdaBoost 是一个最受欢迎的 ML 算法之一。 执行起来非常简单, 并且经常被从业者发现非常有效, 虽然在数学上还是优雅的和理论上的。 AdaBoost 在实践中令人感兴趣的行为仍然令 ML 社区感到困惑。 我们处理算法的稳定性, 并建立了由Rudin、 Daubechies 和 Schapire 于2004 所创的“ Optimal AdaBoost ” 的多重趋同特性。 我们从一个相当强烈的计算意义上证明, 时间平均平均平均几乎是普遍存在的, 并且随着这个过程, 分类者本身的趋同、 其普遍化错误、 以及由此产生的利润差幅, 以及其他许多物体, 使得固定的数据集, 具体地说, 我们把Opatimal AdaBoostbost当作一个动态的系统, 证明我们一般的测算结果, 而我们一般的测算结果, 在一个条件下, 最弱的算法最终, 我们从高度的解算算法的算算算算算算,, 不断更新的周期的周期的周期的周期, 不断的算算法是 的系统, 的精确的系统, 直路的 直路的 直路的显示的 直路的系统, 直路的 直路的 直路的 直路的测的 的 的 的 的 的 的 的 的 直路的 直路的 直路的 直路的 直路的 直路的 直路路的 根 根 根基的 根基的 根基的 根基的 根基的 根基的 直路的 根基的根基的根基的根基的根基的根基的根基的 直路的 直 直到最 根基的 直到我们的 直到我们的 根 根 根基的 根基的根基的 直到我们的 直到我们的根基的 直到最 根的根的 根基的根基的根基的根基的根基的根基的根基的根基的根基的根基的根基的根基的根基