Direct Estimation of Parameters in ODE Models Using WENDy: Weak-form Estimation of Nonlinear Dynamics

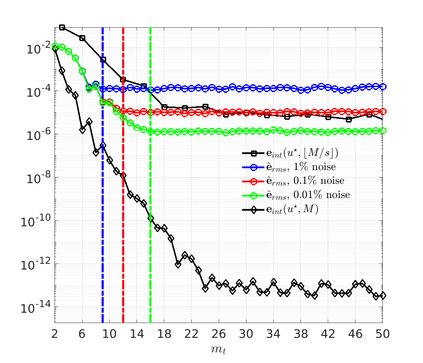
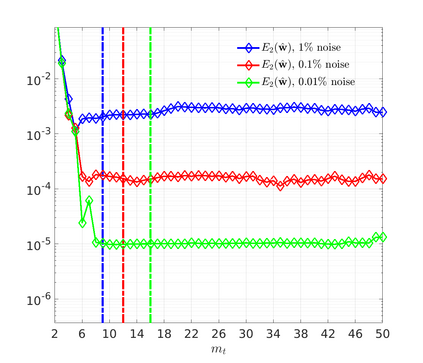
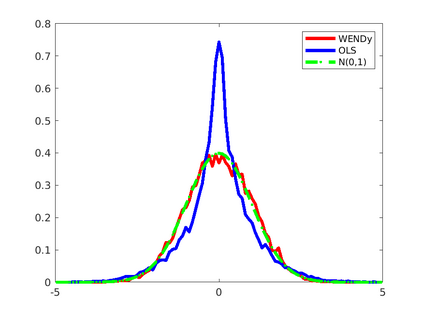
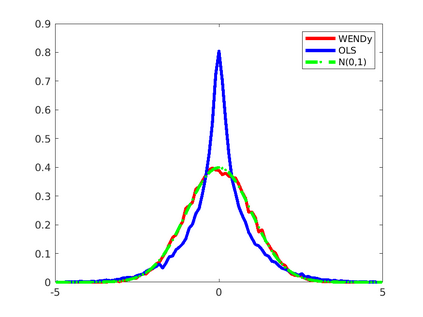
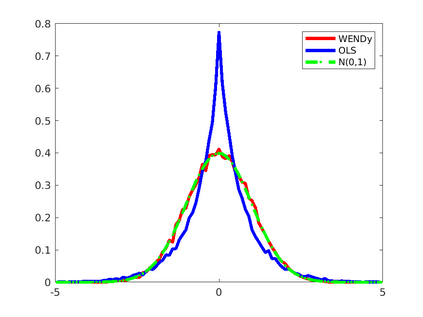
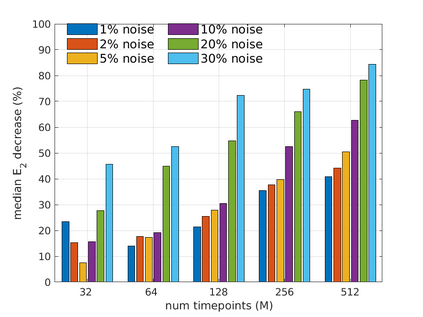
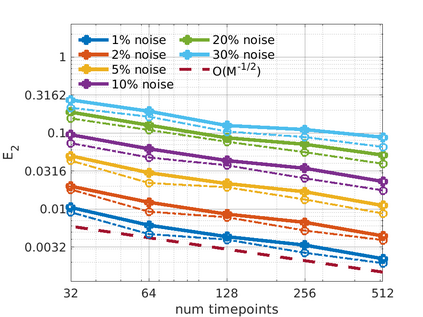
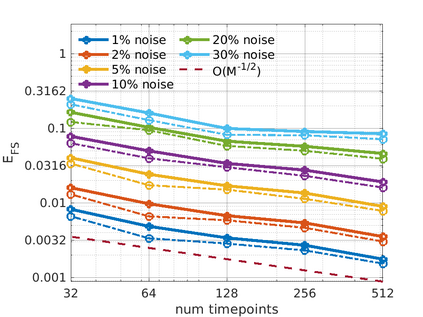
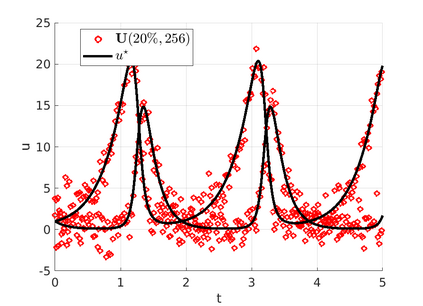
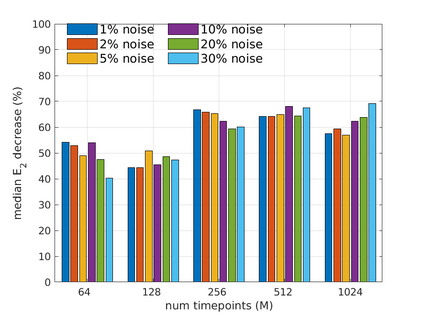
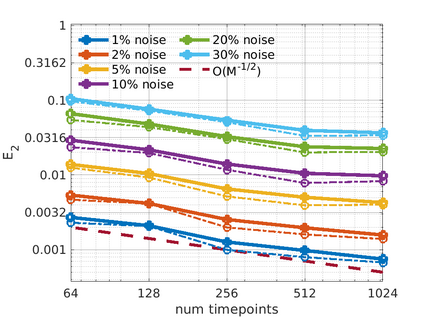
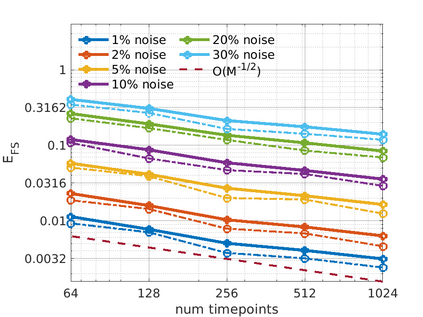
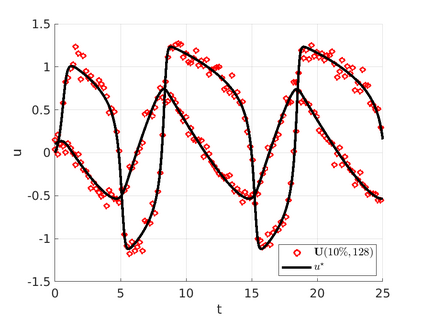
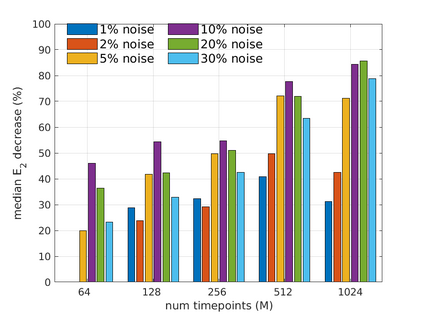
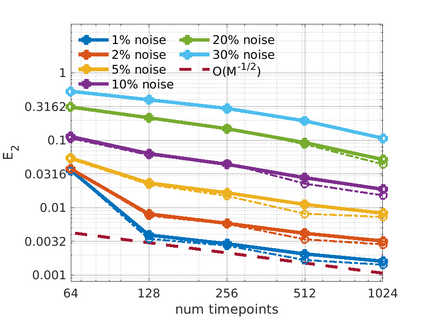
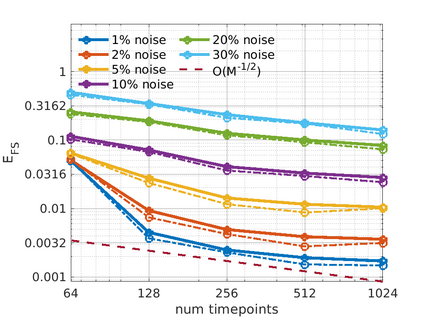
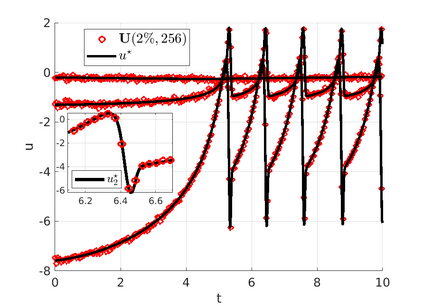
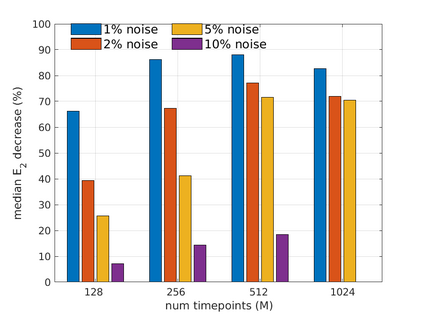
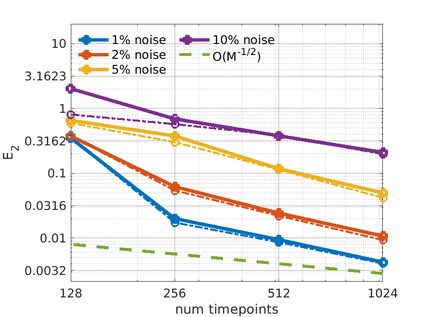
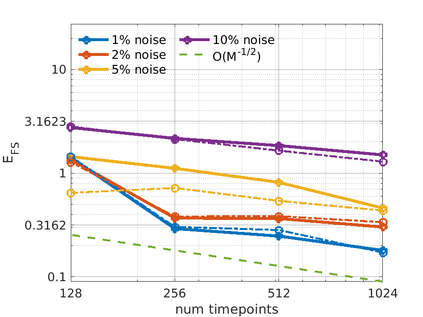
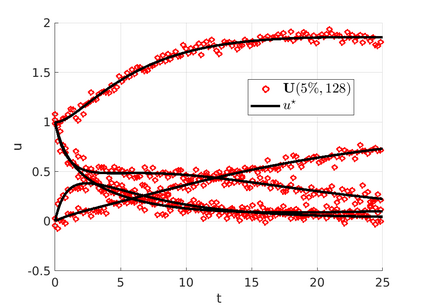
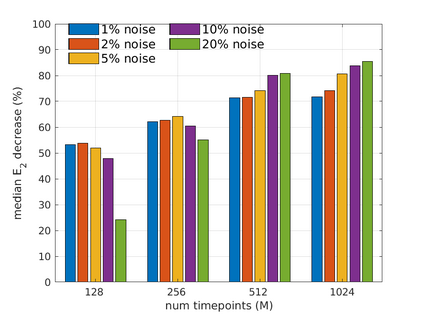
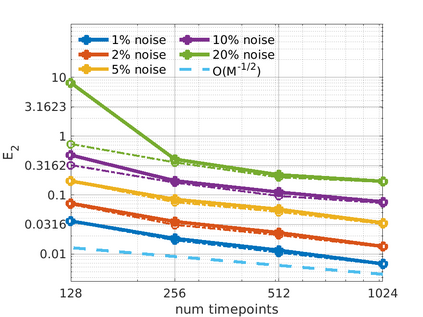
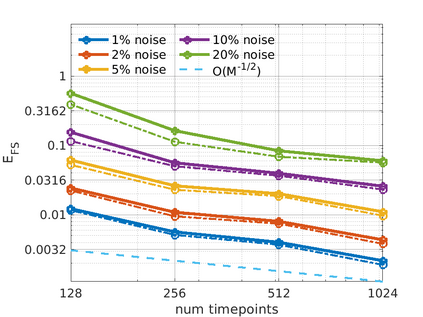
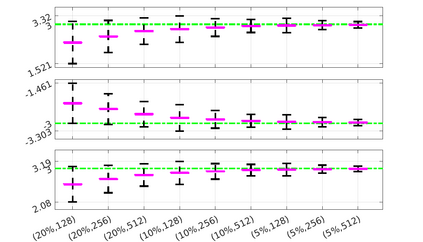
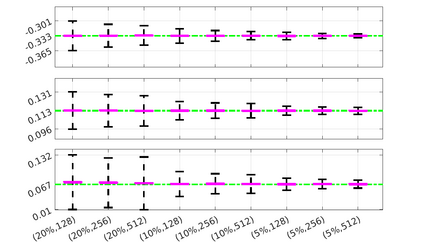
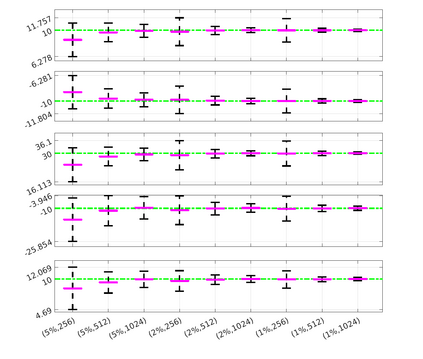
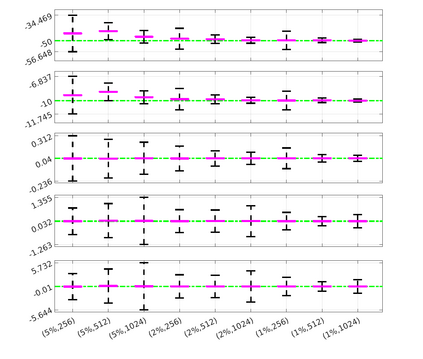
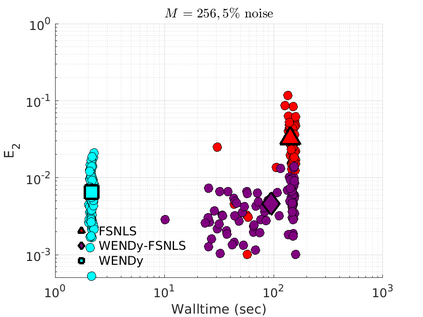
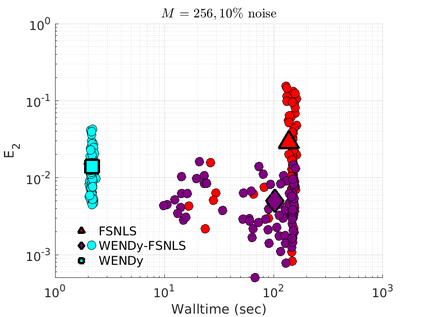
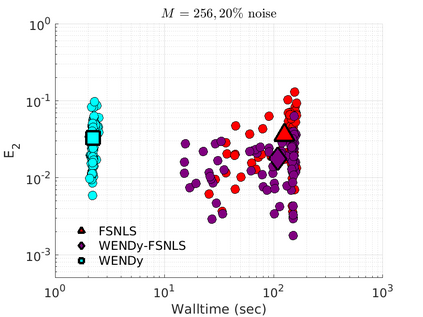
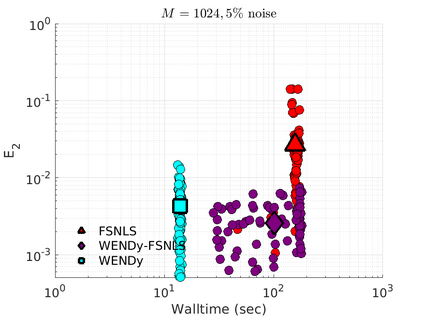
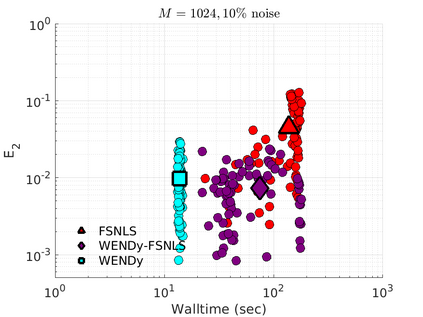
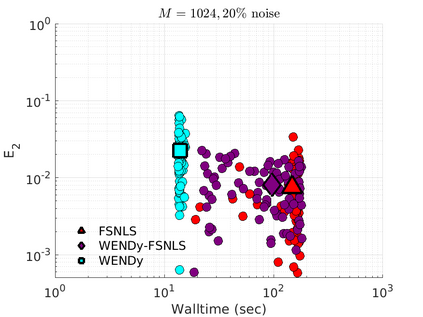
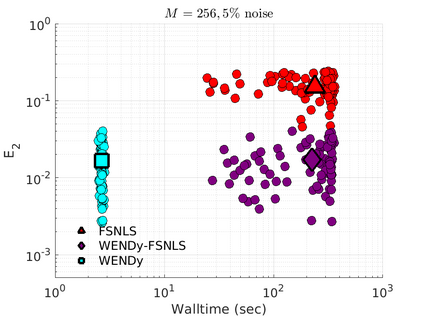
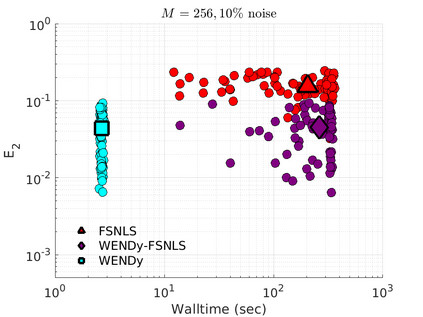
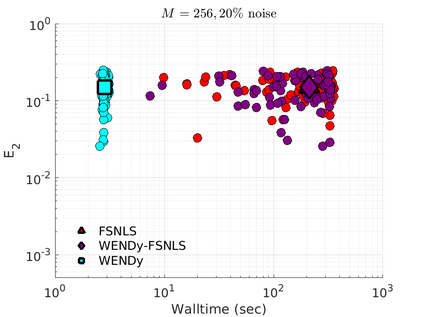
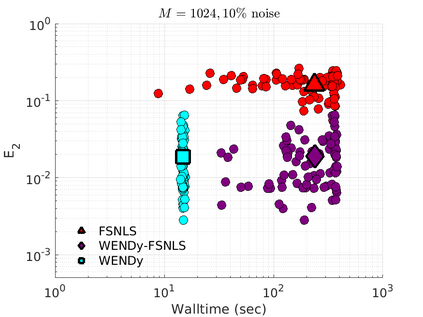
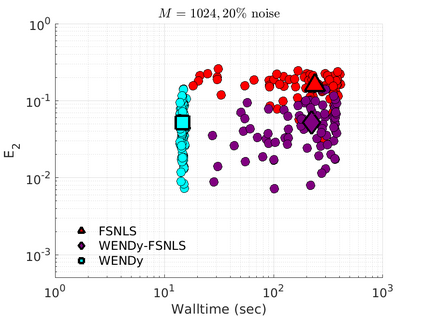
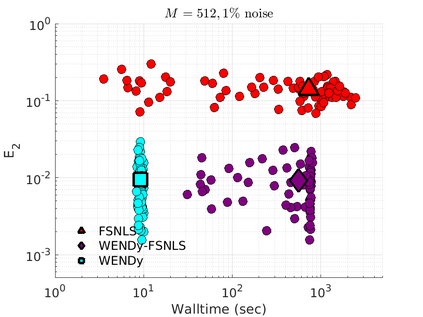
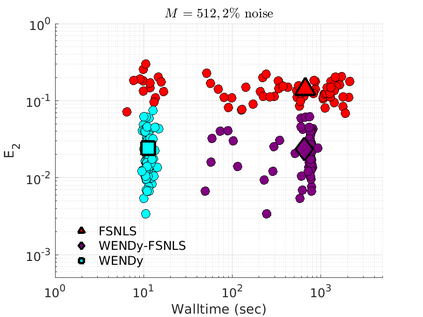
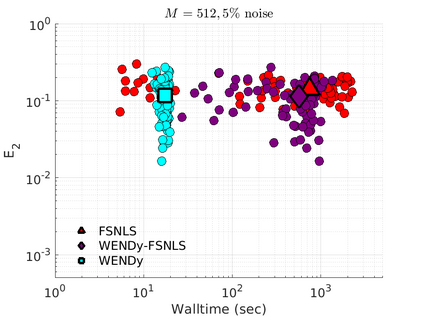
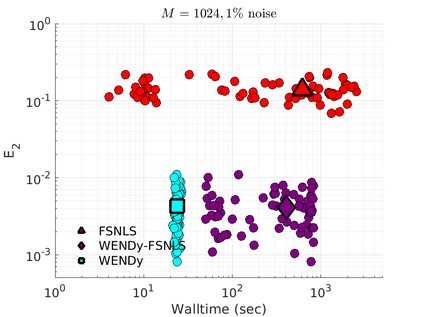
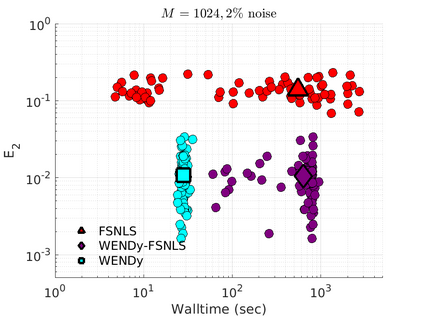
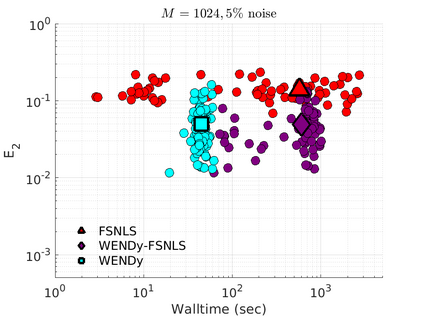
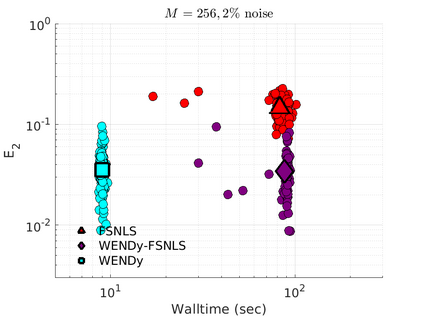
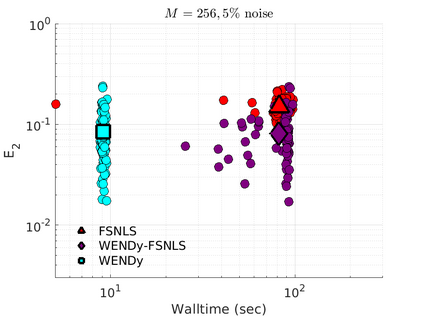
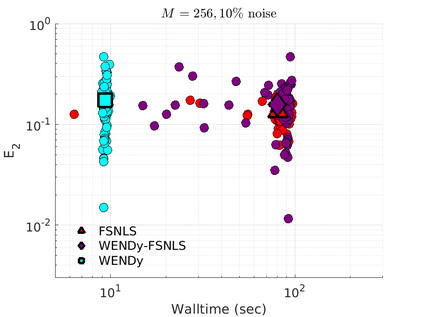
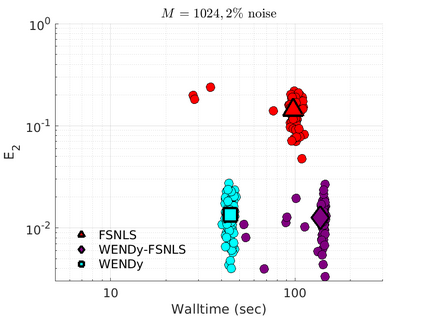
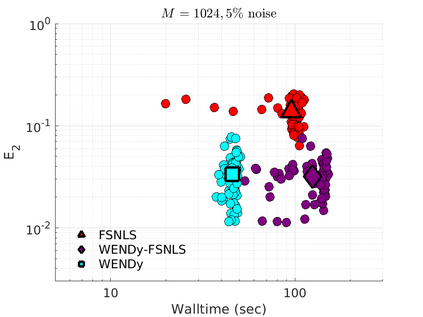
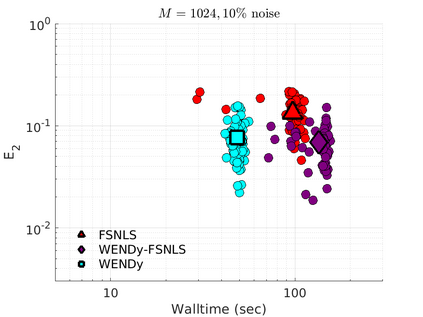
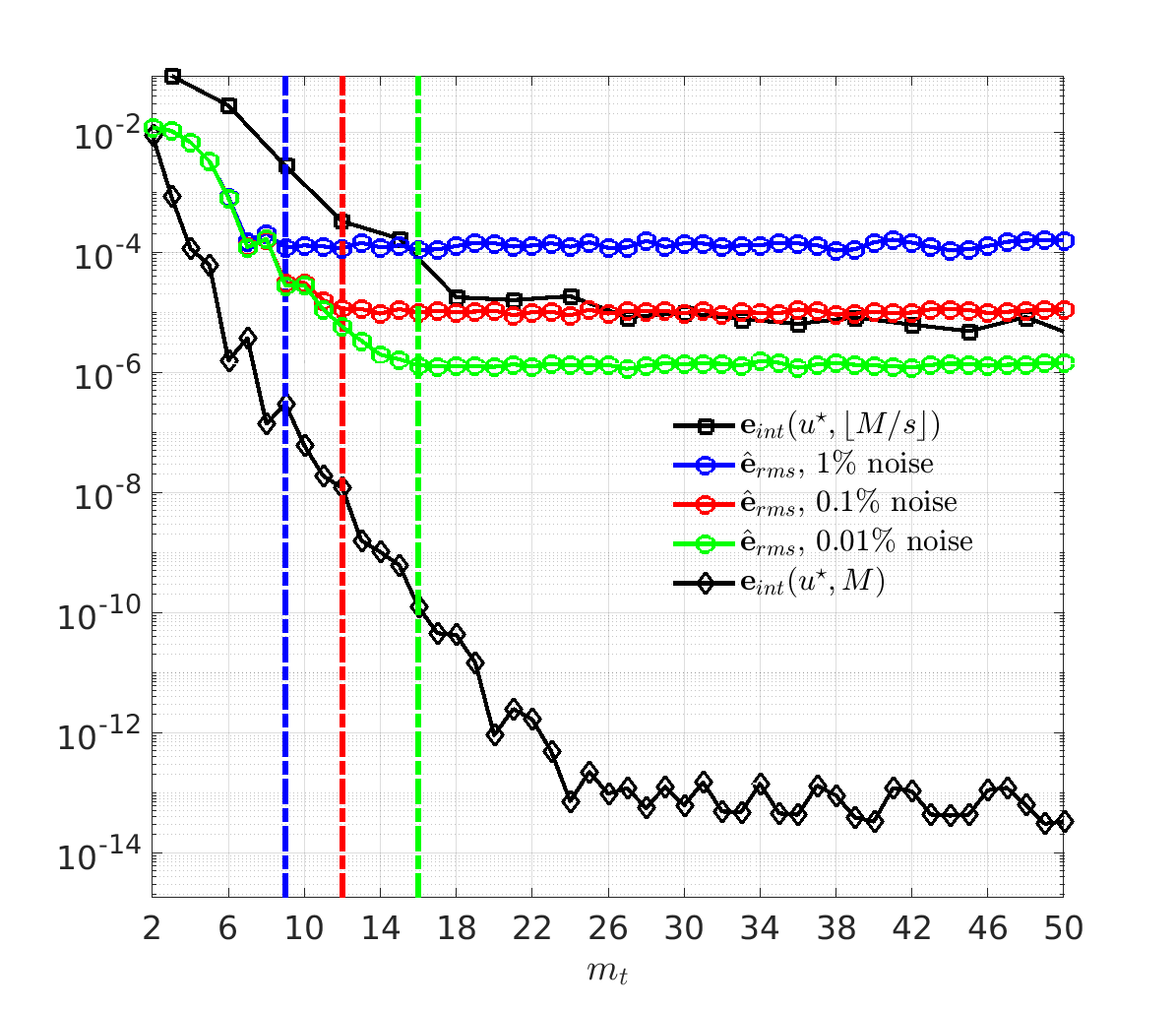
We introduce the Weak-form Estimation of Nonlinear Dynamics (WENDy) method for estimating model parameters for non-linear systems of ODEs. The core mathematical idea involves an efficient conversion of the strong form representation of a model to its weak form, and then solving a regression problem to perform parameter inference. The core statistical idea rests on the Errors-In-Variables framework, which necessitates the use of the iteratively reweighted least squares algorithm. Further improvements are obtained by using orthonormal test functions, created from a set of $C^{\infty}$ bump functions of varying support sizes. We demonstrate that WENDy is a highly robust and efficient method for parameter inference in differential equations. Without relying on any numerical differential equation solvers, WENDy computes accurate estimates and is robust to large (biologically relevant) levels of measurement noise. For low dimensional systems with modest amounts of data, WENDy is competitive with conventional forward solver-based nonlinear least squares methods in terms of speed and accuracy. For both higher dimensional systems and stiff systems, WENDy is typically both faster (often by orders of magnitude) and more accurate than forward solver-based approaches. We illustrate the method and its performance in some common population and neuroscience models, including logistic growth, Lotka-Volterra, FitzHugh-Nagumo, Hindmarsh-Rose, and a Protein Transduction Benchmark model. Software and code for reproducing the examples is available at (https://github.com/MathBioCU/WENDy).