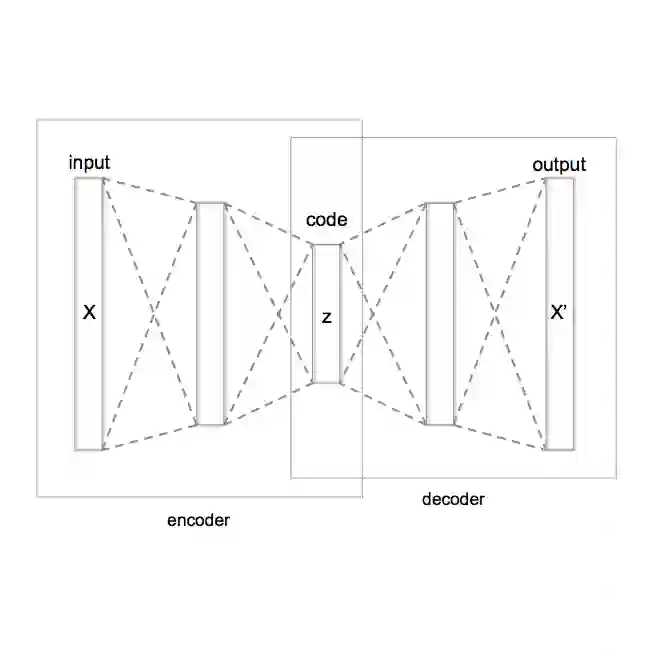
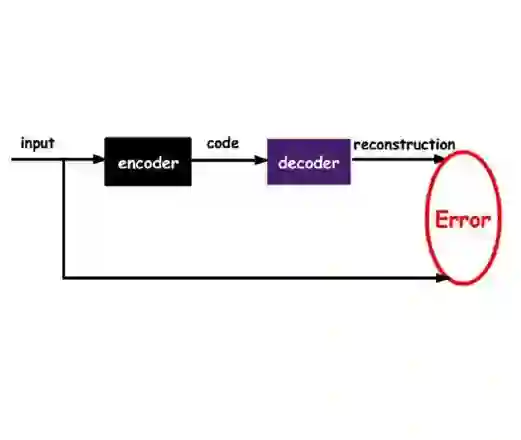
Although the variational autoencoder (VAE) and its conditional extension (CVAE) are capable of state-of-the-art results across multiple domains, their precise behavior is still not fully understood, particularly in the context of data (like images) that lie on or near a low-dimensional manifold. For example, while prior work has suggested that the globally optimal VAE solution can learn the correct manifold dimension, a necessary (but not sufficient) condition for producing samples from the true data distribution, this has never been rigorously proven. Moreover, it remains unclear how such considerations would change when various types of conditioning variables are introduced, or when the data support is extended to a union of manifolds (e.g., as is likely the case for MNIST digits and related). In this work, we address these points by first proving that VAE global minima are indeed capable of recovering the correct manifold dimension. We then extend this result to more general CVAEs, demonstrating practical scenarios whereby the conditioning variables allow the model to adaptively learn manifolds of varying dimension across samples. Our analyses, which have practical implications for various CVAE design choices, are also supported by numerical results on both synthetic and real-world datasets.
翻译:虽然变式自动编码器(VAE)及其有条件的扩展(CVAE)能够在不同领域取得最新的最新结果,但是它们的确切行为仍然没有得到完全理解,特别是在低维元上或接近低维元的数据(图像)方面。例如,先前的工作表明,全球最佳的VAE解决方案可以学习正确的多维度,这是从真实数据分布中制作样本的必要(但并非足够)条件,但从未得到严格证明。此外,在采用各种类型的调节变量或数据支持扩大到多个元的组合(例如,对MMIST数字和相关数据可能存在的情况)时,这些考虑因素将如何改变。在这项工作中,我们首先通过证明VAE全球微型模型确实能够恢复正确的多维度,然后将这一结果推广到更普遍的CVAE,表明调节变量允许模型适应性地学习不同层面的多维度的实用假设。我们对各种CVAE模型的实际影响以及各种合成数据都得到真实数字结果的支持。