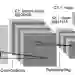
In this paper we investigate the use of Fourier Neural Operators (FNOs) for image classification in comparison to standard Convolutional Neural Networks (CNNs). Neural operators are a discretization-invariant generalization of neural networks to approximate operators between infinite dimensional function spaces. FNOs - which are neural operators with a specific parametrization - have been applied successfully in the context of parametric PDEs. We derive the FNO architecture as an example for continuous and Fr\'echet-differentiable neural operators on Lebesgue spaces. We further show how CNNs can be converted into FNOs and vice versa and propose an interpolation-equivariant adaptation of the architecture.
翻译:在本文中,我们比较了傅里叶神经算子(Fourier Neural Operators,FNOs)与标准的卷积神经网络(Convolutional Neural Networks,CNNs)在图像分类上的应用。神经算子是神经网络到无穷维函数空间中算子近似的一种去离散化的泛化方法。FNOs 是一个具有特定参数化的神经算子,已经成功地应用于参数化偏微分方程的上下文中。我们通过一些连续和 Fr\'echet 可微的神经算子在勒贝格空间中,推导了 FNO 架构。我们进一步展示了CNNs可转换为FNOs,反之亦然,并提出了一种插值等变的适应方法。