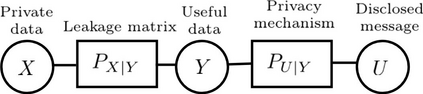
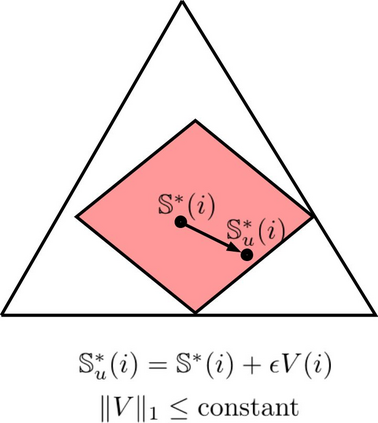
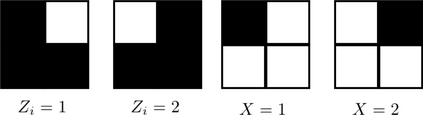
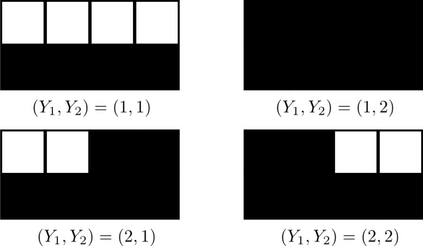
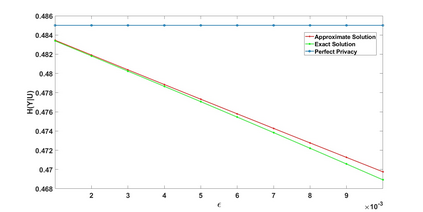
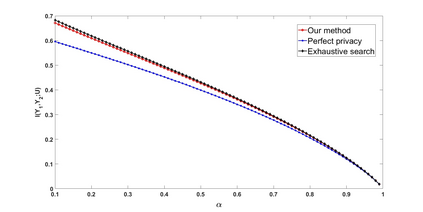
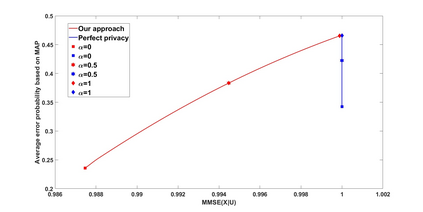
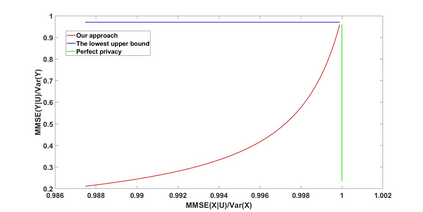
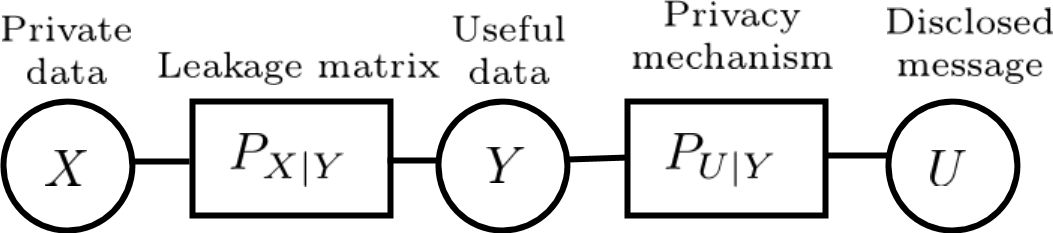
We study a statistical signal processing privacy problem, where an agent observes useful data $Y$ and wants to reveal the information to a user. Since the useful data is correlated with the private data $X$, the agent employs a privacy mechanism to generate data $U$ that can be released. We study the privacy mechanism design that maximizes the revealed information about $Y$ while satisfying a strong $\ell_1$-privacy criterion. When a sufficiently small leakage is allowed, we show that the optimizer vectors of the privacy mechanism design problem have a specific geometry, i.e., they are perturbations of fixed vector distributions. This geometrical structure allows us to use a local approximation of the conditional entropy. By using this approximation the original optimization problem can be reduced to a linear program so that an approximate solution for privacy mechanism can be easily obtained. The main contribution of this work is to consider non-zero leakage with a non-invertible leakage matrix. In an example inspired by water mark application, we first investigate the accuracy of the approximation. Then, we employ different measures for utility and privacy leakage to compare the privacy-utility trade-off using our approach with other methods. In particular, it has been shown that by allowing small leakage, significant utility can be achieved using our method compared to the case where no leakage is allowed.
翻译:我们研究一个统计信号处理隐私问题,其中代理商观测有用的数据,但希望向用户披露有关信息。由于有用的数据与私人数据挂钩,该代理商使用一个隐私机制生成能够释放的数据美元美元。我们研究一个隐私机制设计,在满足强烈的1美元1美元隐私标准的同时,将披露的信息最大化。当允许足够小的渗漏时,我们显示,隐私机制设计问题的最佳矢量具有特定的几何,即它们是固定矢量分布的干扰。这一几何结构允许我们使用一个本地的有条件的矢量分布近似。通过使用这一近似,最初的优化问题可以降低为线性程序,这样可以很容易地获得对隐私机制的近似解决办法。这项工作的主要贡献是考虑非零渗漏,使用非垂直的渗漏矩阵。在水标记应用的启发下,我们首先调查近差的准确性。然后,我们使用不同的实用性和隐私渗漏措施来比较有条件的诱导的诱导。通过使用显著的渗漏方法,我们无法使用其他的方法来比较重要的渗漏法。