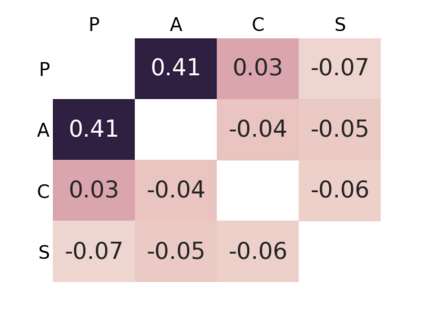
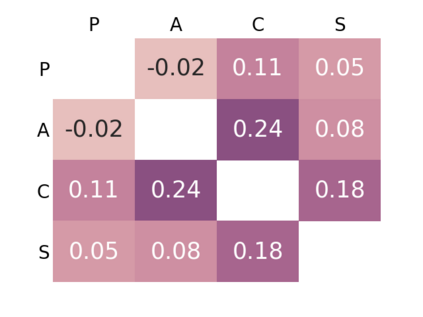
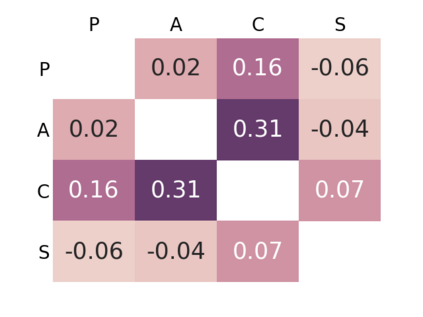
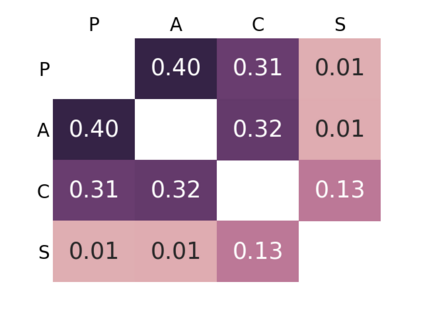
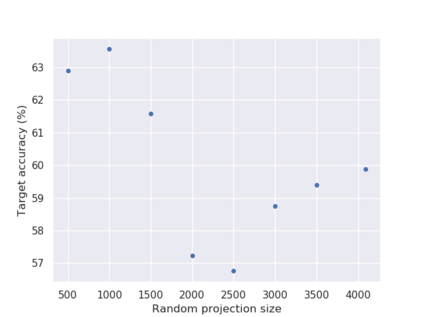
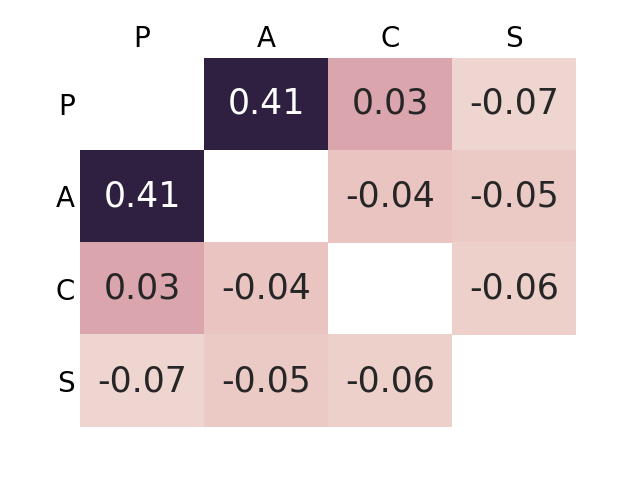
Supervised learning results typically rely on assumptions of i.i.d. data. Unfortunately, those assumptions are commonly violated in practice. In this work, we tackle such problem by focusing on domain generalization: a formalization where the data generating process at test time may yield samples from never-before-seen domains (distributions). Our work relies on the following lemma: by minimizing a notion of discrepancy between all pairs from a set of given domains, we also minimize the discrepancy between any pairs of mixtures of domains. Using this result, we derive a generalization bound for our setting. We then show that low risk over unseen domains can be achieved by representing the data in a space where (i) the training distributions are indistinguishable, and (ii) relevant information for the task at hand is preserved. Minimizing the terms in our bound yields an adversarial formulation which estimates and minimizes pairwise discrepancies. We validate our proposed strategy on standard domain generalization benchmarks, outperforming a number of recently introduced methods. Notably, we tackle a real-world application where the underlying data corresponds to multi-channel electroencephalography time series from different subjects, each considered as a distinct domain.
翻译:受监督的学习结果通常依赖于i. id. 数据的假设。 不幸的是,这些假设在实践上通常被违反。 在这项工作中,我们通过侧重于领域一般化来解决这个问题:一个正规化的过程,测试时的数据生成过程可能从从未见的域(分布)中产生样本。我们的工作依赖于以下列姆马:通过将一组特定域的所有对子之间的差异概念最小化,我们还最大限度地缩小了对一组特定域的所有对子之间的差异。使用这一结果,我们为我们的设置得出了一种通用化。然后,我们通过在以下空间中代表数据,可以实现对隐蔽域的低风险:(一) 培训分布是无法分辨的,以及(二) 保留与手头任务相关的信息。我们结合的术语产生一种对抗性配方,该配方估计和尽量减少相对的差异。我们验证了我们关于标准域一般化基准的拟议战略,比最近采用的一些方法要好。值得注意的是,我们在现实世界应用中,基础数据与不同主题的多声波断时间序列相对。