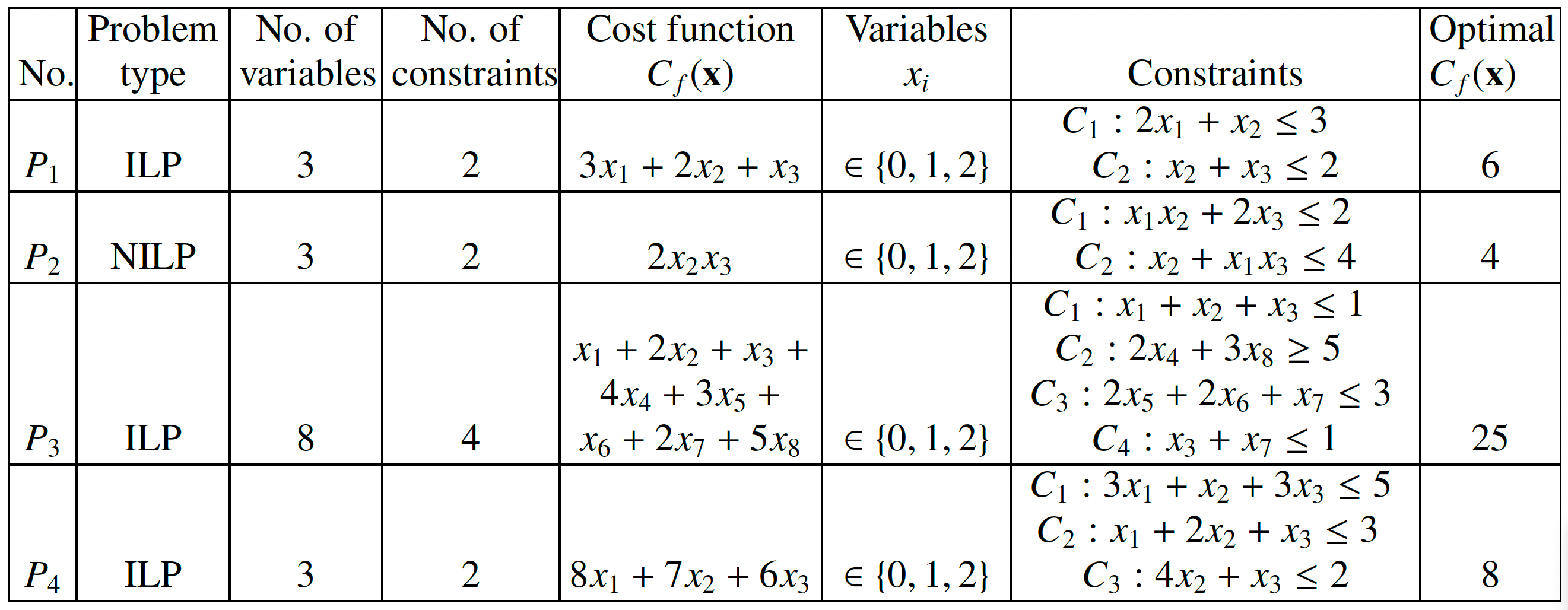
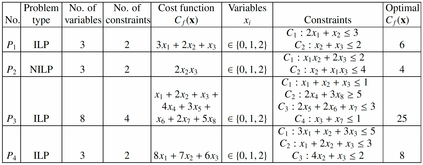
Integer Programming Using A Single Atom

Integer programming (IP), as the name suggests is an integer-variable-based approach commonly used to formulate real-world optimization problems with constraints. Currently, quantum algorithms reformulate the IP into an unconstrained form through the use of binary variables, which is an indirect and resource-consuming way of solving it. We develop an algorithm that maps and solves an IP problem in its original form to any quantum system that possesses a large number of accessible internal degrees of freedom which can be controlled with sufficient accuracy. Using a single Rydberg atom as an example, we associate the integer values to electronic states belonging to different manifolds and implement a selective superposition of these different states to solve the full IP problem. The optimal solution is found within 2-40{\mu}s for a few prototypical IP problems with up to eight variables and up to four constraints including a non-linear IP problem, which is usually harder to solve with classical algorithms when compared with linear IP problems. Our algorithm for solving IP is benchmarked using the Branch & Bound approach and it outperforms the classical algorithm in terms of the number of steps needed to converge and carries the potential to improve the bounds provided by the classical algorithm for larger problems.