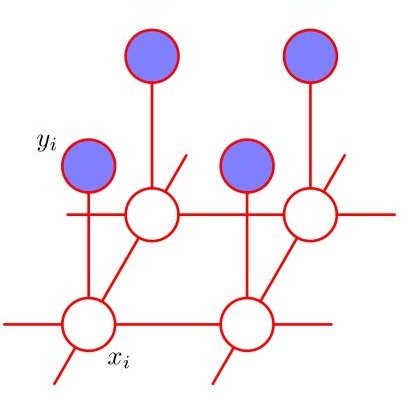
The paper introduces the application of information geometry to describe the ground states of Ising models by utilizing parity-check matrices of cyclic and quasi-cyclic codes on toric and spherical topologies. The approach establishes a connection between machine learning and error-correcting coding. This proposed approach has implications for the development of new embedding methods based on trapping sets. Statistical physics and number geometry applied for optimize error-correcting codes, leading to these embedding and sparse factorization methods. The paper establishes a direct connection between DNN architecture and error-correcting coding by demonstrating how state-of-the-art architectures (ChordMixer, Mega, Mega-chunk, CDIL, ...) from the long-range arena can be equivalent to of block and convolutional LDPC codes (Cage-graph, Repeat Accumulate). QC codes correspond to certain types of chemical elements, with the carbon element being represented by the mixed automorphism Shu-Lin-Fossorier QC-LDPC code. The connections between Belief Propagation and the Permanent, Bethe-Permanent, Nishimori Temperature, and Bethe-Hessian Matrix are elaborated upon in detail. The Quantum Approximate Optimization Algorithm (QAOA) used in the Sherrington-Kirkpatrick Ising model can be seen as analogous to the back-propagation loss function landscape in training DNNs. This similarity creates a comparable problem with TS pseudo-codeword, resembling the belief propagation method. Additionally, the layer depth in QAOA correlates to the number of decoding belief propagation iterations in the Wiberg decoding tree. Overall, this work has the potential to advance multiple fields, from Information Theory, DNN architecture design (sparse and structured prior graph topology), efficient hardware design for Quantum and Classical DPU/TPU (graph, quantize and shift register architect.) to Materials Science and beyond.
翻译:暂无翻译