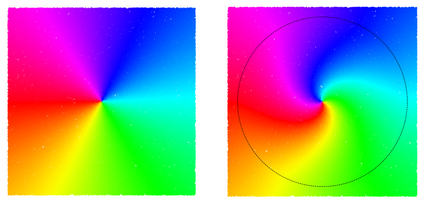
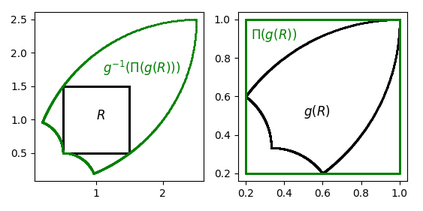
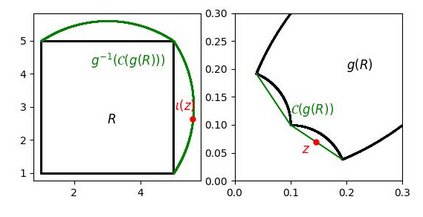
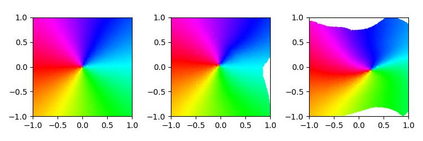
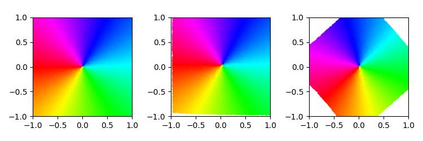
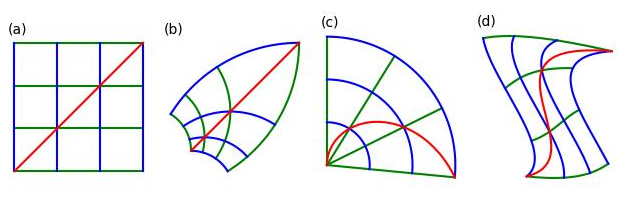
Unsupervised learning of latent variable models (LVMs) is widely used to represent data in machine learning. When such models reflect the ground truth factors and the mechanisms mapping them to observations, there is reason to expect that they allow generalization in downstream tasks. It is however well known that such identifiability guaranties are typically not achievable without putting constraints on the model class. This is notably the case for nonlinear Independent Component Analysis, in which the LVM maps statistically independent variables to observations via a deterministic nonlinear function. Several families of spurious solutions fitting perfectly the data, but that do not correspond to the ground truth factors can be constructed in generic settings. However, recent work suggests that constraining the function class of such models may promote identifiability. Specifically, function classes with constraints on their partial derivatives, gathered in the Jacobian matrix, have been proposed, such as orthogonal coordinate transformations (OCT), which impose orthogonality of the Jacobian columns. In the present work, we prove that a subclass of these transformations, conformal maps, is identifiable and provide novel theoretical results suggesting that OCTs have properties that prevent families of spurious solutions to spoil identifiability in a generic setting.
翻译:对潜伏变量模型(LVMs)的未经监督的学习被广泛用于在机器学习中代表数据。当这些模型反映地面真相因素和将其映射为观测机制时,有理由期望这些模型能够对下游任务进行概括化。然而,众所周知,在不限制模型类的情况下,这种可识别性保障通常无法实现。在非线性独立组成部分分析中,LVM绘制了通过确定性的非线性非线性功能进行观测的统计独立的变量图。一些模棱两可的解决方案家庭,完全适合数据,但不符合地面真相因素的,可以在通用环境中构建。然而,最近的工作表明,限制这类模型的功能类别可能会促进可识别性。具体地说,有人提议了对部分衍生物有限制的分类,这些分类在雅各基矩阵中收集,例如,可图式协调变式变形(OCT),这些变形将雅各列的变形或多义性地强加于人。在目前的工作中,我们证明,这些变形的子小类,即符合地图,可识别,并提供新的理论结果显示OCT可预期性。