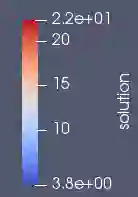
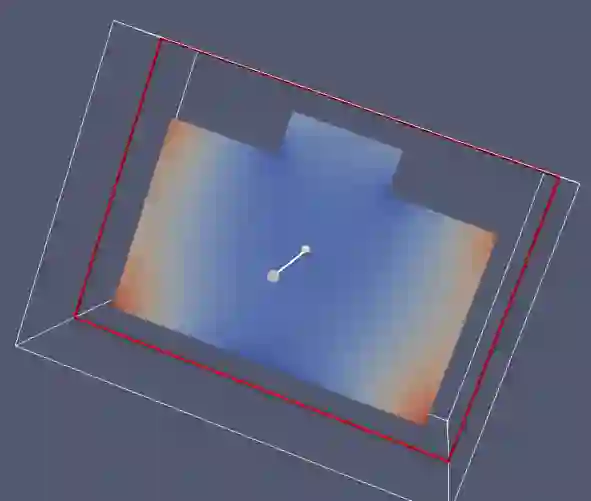
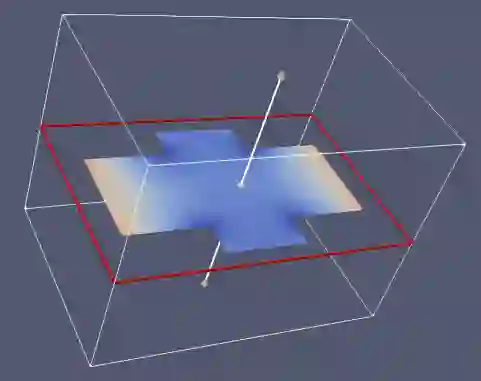
Partial Differential Equations (PDEs) describe several problems relevant to many fields of applied sciences, and their discrete counterparts typically involve the solution of sparse linear systems. In this context, we focus on the analysis of the computational aspects related to the solution of large and sparse linear systems with HPC solvers, by considering the performances of direct and iterative solvers in terms of computational efficiency, scalability, and numerical accuracy. Our aim is to identify the main criteria to support application-domain specialists in the selection of the most suitable solvers, according to the application requirements and available resources. To this end, we discuss how the numerical solver is affected by the regular/irregular discretisation of the input domain, the discretisation of the input PDE with piecewise linear or polynomial basis functions, which generally result in a higher/lower sparsity of the coefficient matrix, and the choice of different initial conditions, which are associated with linear systems with multiple right-hand side terms. Finally, our analysis is independent of the characteristics of the underlying computational architectures, and provides a methodological approach that can be applied to different classes of PDEs or with approximation problems.
翻译:部分均衡(PDEs)描述与应用科学许多领域有关的若干问题,其离散对应方通常涉及稀散线性系统的解决办法。在这方面,我们侧重于分析与高聚苯乙烯溶解器有关的大型和稀散线性系统解决办法的计算方面,方法是从计算效率、可缩放性和数字准确性等方面考虑直接和迭代解决器的性能。我们的目的是根据应用要求和现有资源,确定支持应用领域专家选择最合适的解决器的主要标准。为此,我们讨论了数字解答器如何受到输入领域经常/不定期离散的影响,投入PDE与小线性线性系统相关联的分解线性或多面基功能,通常导致系数矩阵的较高/较低宽度,以及选择不同的初始条件,这些条件与具有多重右侧条件的线性系统有关。最后,我们的分析独立于基本计算结构的特点,并提供了一种方法方法,可适用于不同类别的PDE或近似问题。