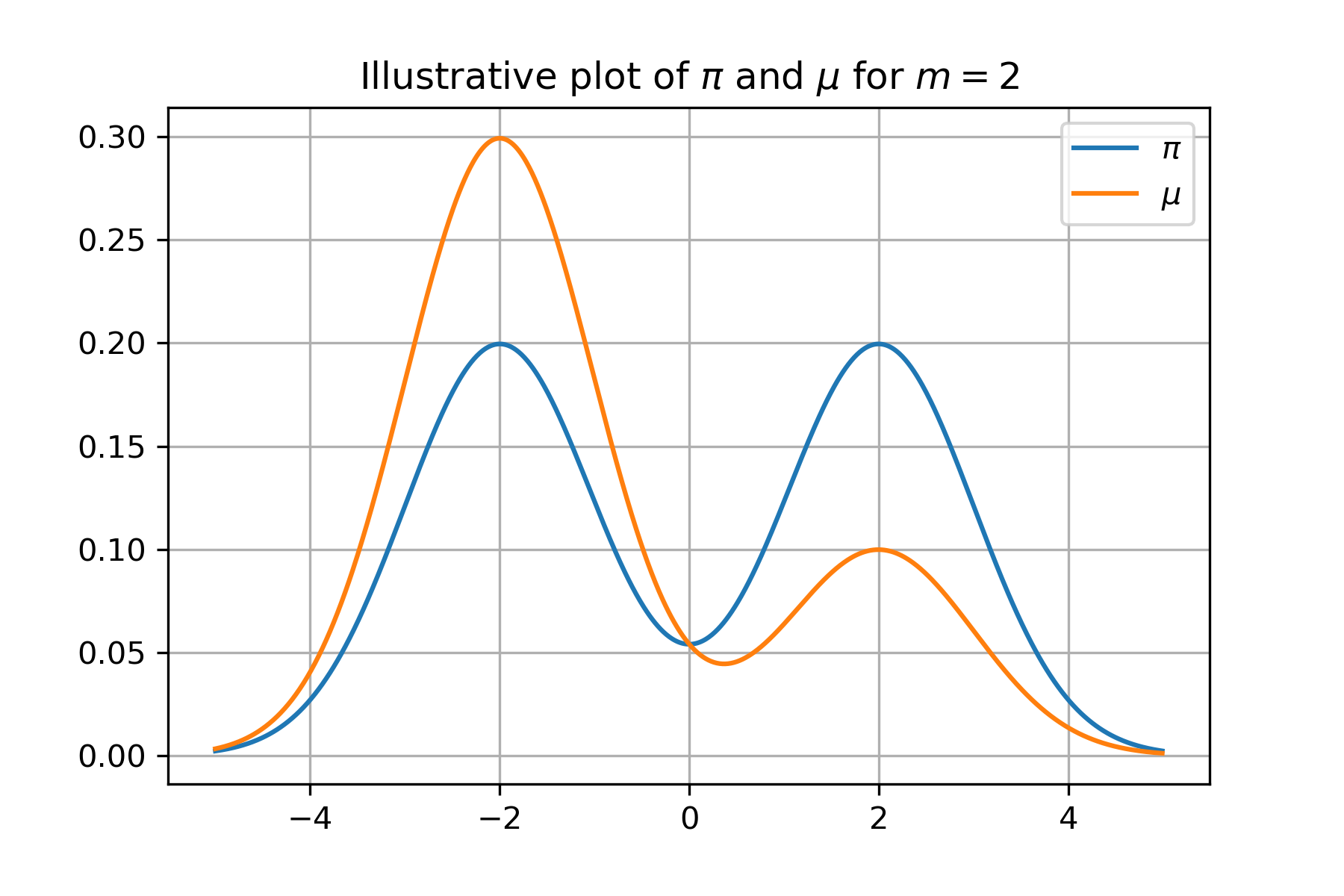
For the task of sampling from a density $\pi \propto \exp(-V)$ on $\mathbb{R}^d$, where $V$ is possibly non-convex but $L$-gradient Lipschitz, we prove that averaged Langevin Monte Carlo outputs a sample with $\varepsilon$-relative Fisher information after $O( L^2 d^2/\varepsilon^2)$ iterations. This is the sampling analogue of complexity bounds for finding an $\varepsilon$-approximate first-order stationary points in non-convex optimization and therefore constitutes a first step towards the general theory of non-log-concave sampling. We discuss numerous extensions and applications of our result; in particular, it yields a new state-of-the-art guarantee for sampling from distributions which satisfy a Poincar\'e inequality.
翻译:对于从一个密度$\pi\ propto\ exp(-V)$\ exp(-V)$\ mathb{R ⁇ d$( V$) 的样本任务,其中V$可能是非混凝土的,但Lipschitz 美元,我们证明,平均Langevin Monte Carlo在用美元(L ⁇ 2 d ⁇ 2/\ varepsilon=2美元)之后,以瓦列普斯隆(- V) 的相对渔业信息作为样本。这是在非混凝土优化中找到一个近于一级固定点的复杂界限的样本,因此是朝着非混凝土取样的一般理论迈出的第一步。我们讨论了我们结果的许多扩展和应用;特别是,它产生了一种满足Poincar(Poincar) 不平等的分布中取样的新型先进保证。