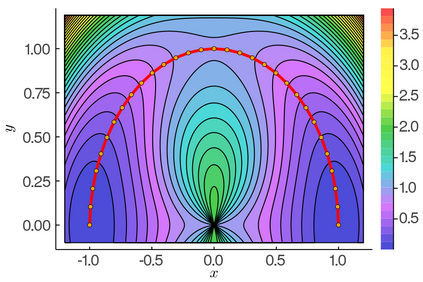
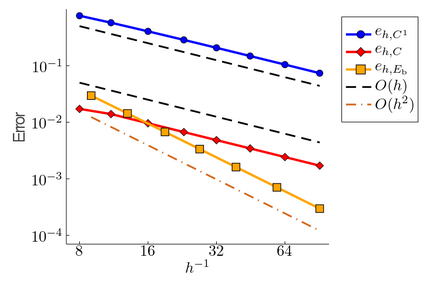
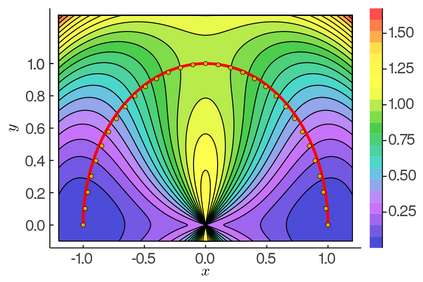
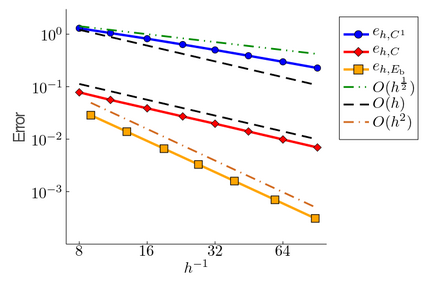
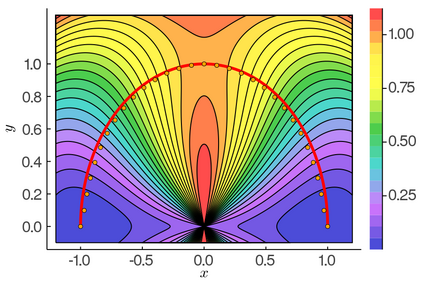
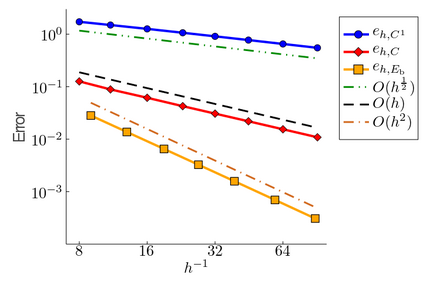
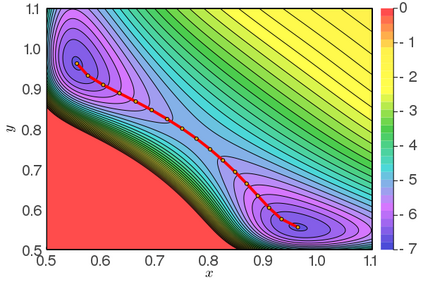
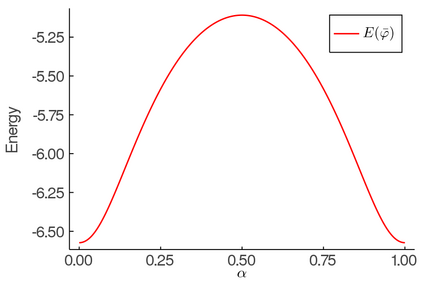
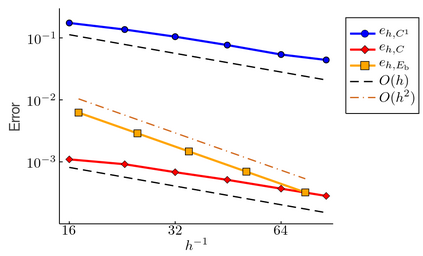
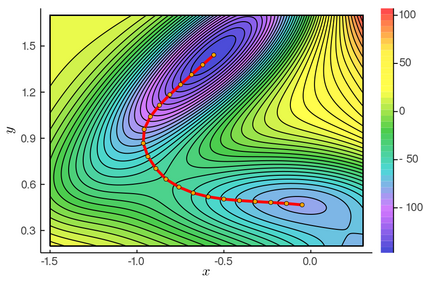
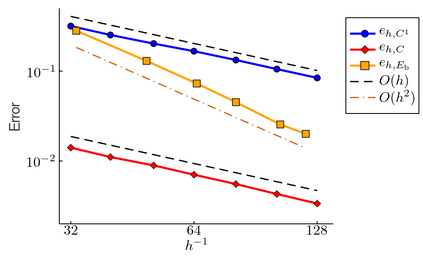
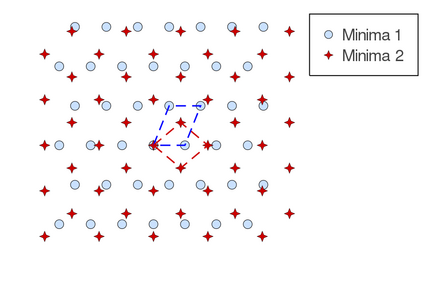
The minimum energy path (MEP) describes the mechanism of reaction, and the energy barrier along the path can be used to calculate the reaction rate in thermal systems. The nudged elastic band (NEB) method is one of the most commonly used schemes to compute MEPs numerically. It approximates an MEP by a discrete set of configuration images, where the discretization size determines both computational cost and accuracy of the simulations. In this paper, we consider a discrete MEP to be a stationary state of the NEB method and prove an optimal convergence rate of the discrete MEP with respect to the number of images. Numerical simulations for the transitions of some several proto-typical model systems are performed to support the theory.
翻译:最小能量路径(MEP) 描述反应机制, 沿路径的能量屏障可以用来计算热系统的反应率。 振动弹性带( NEB) 方法是用数字计算MEP的最常用办法之一。 它通过一组离散的配置图象对MEP进行近似, 其中离散的尺寸决定了模拟的计算成本和准确性。 在本文中, 我们认为离散的MEP 是 NEB 方法的固定状态, 并证明离散的MEP 在图像数量上是最佳的趋同率 。 为了支持这一理论, 对一些原型模型系统的转型进行了数字模拟 。