Sum-Rate Optimal Relay Selection and Power Control in Multi-Hop Networks

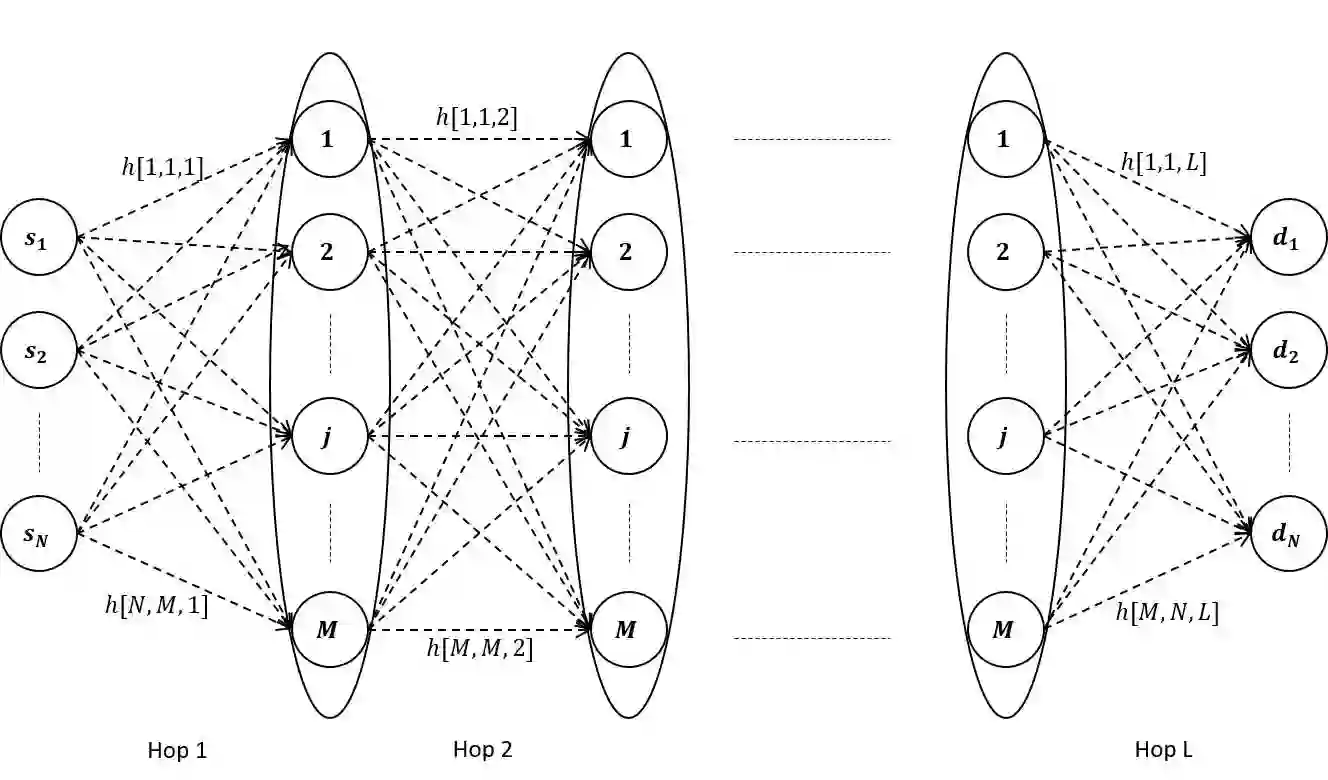
In this paper, we focus on the achievable sum-rate optimization problem of a multi-user, multi-hop relay network. We analyze the joint relay selection and power control in the presence of interference such that the achievable sum-rate is maximized. First, we evaluate the achievable sum-rate under five relay selection strategies when the transmit power is fixed. We show that the dynamic programming based max-min relay selection with the objective of maximizing the minimum signal-to-noise-ratio results in the highest achievable sum-rate gain for larger networks. Next, we combine the relay selection problem using the max-min relay selection and the power control problem using a tight lower bound approximation and propose a novel iterative algorithm, which maximizes the achievable sum-rate. We also provide a comprehensive comparison of the proposed algorithm with respect to existing resource allocation techniques, and observe that our proposed algorithm provides significant sum-rate gains. Finally, we prove that for the special case of two-user networks, binary power allocation is optimum for at least two transmitting nodes. Extensive numerical examples are provided to illustrate the accuracy of our results.