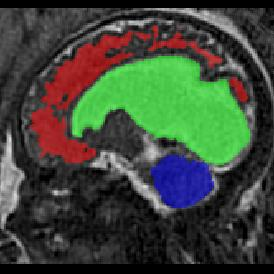
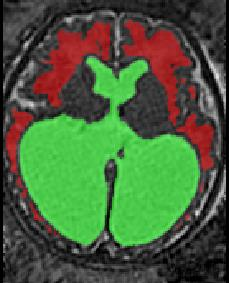
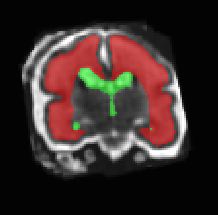
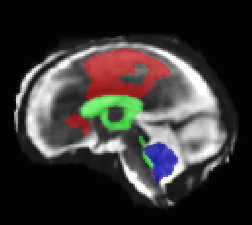
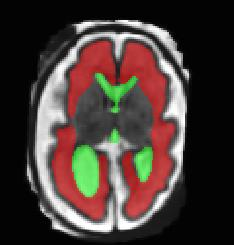
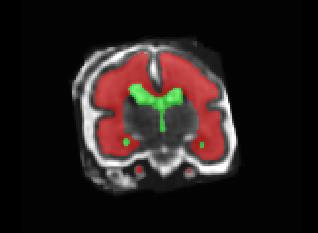
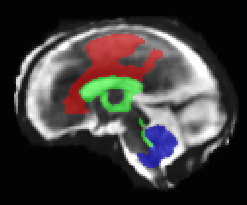
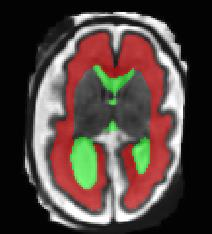
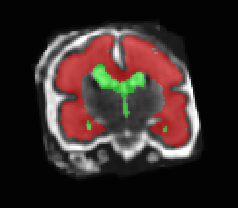
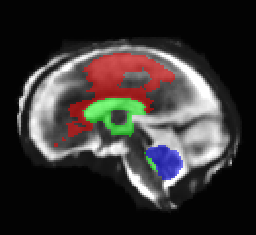
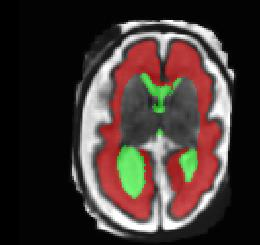
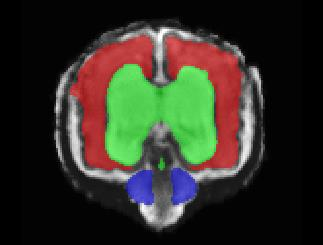
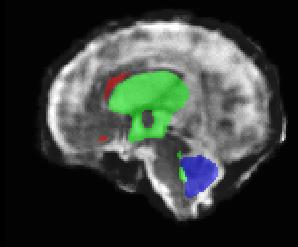
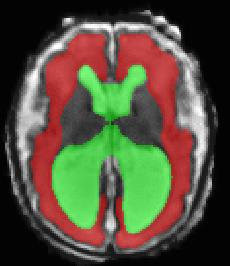
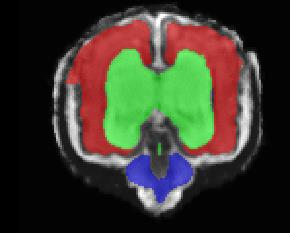
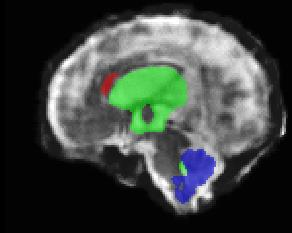
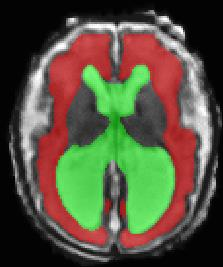
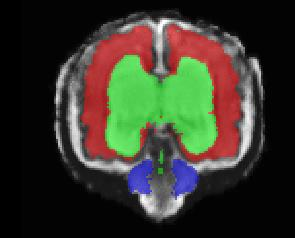
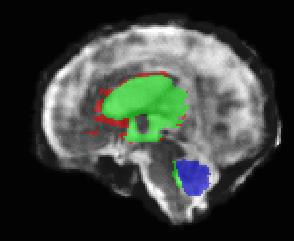
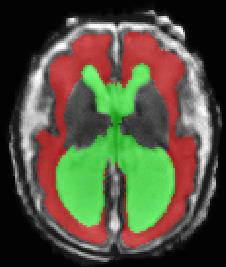
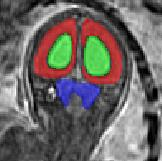
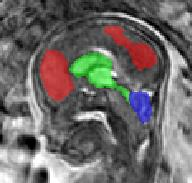
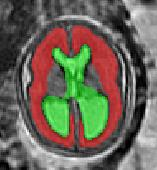
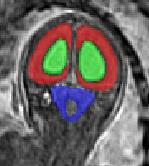
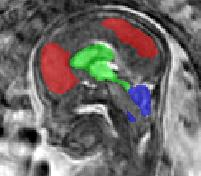
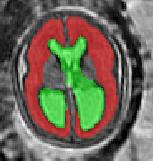
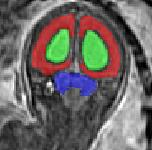
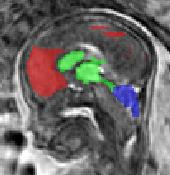
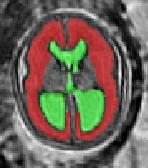
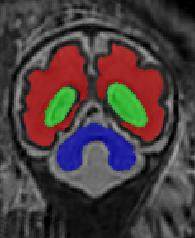
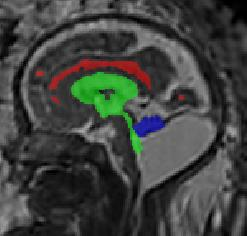
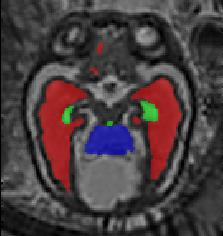
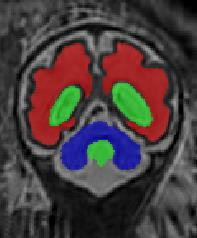
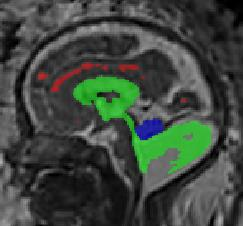
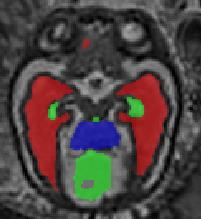
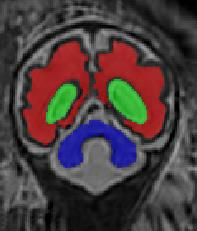
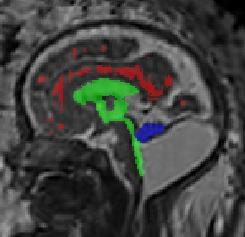
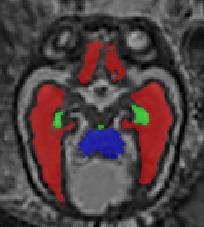
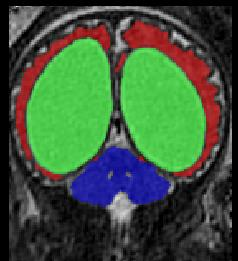
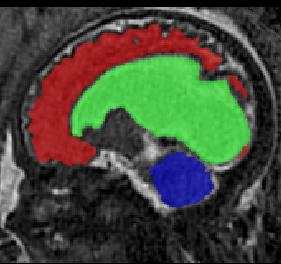
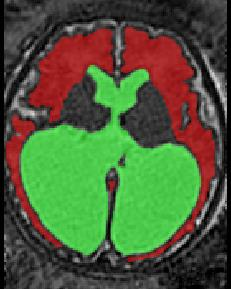
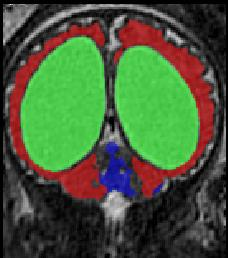
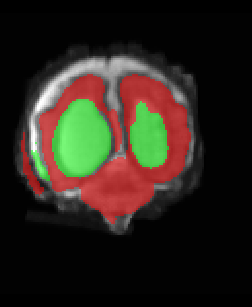
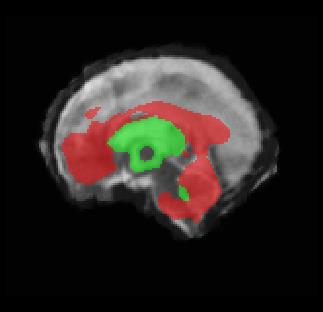
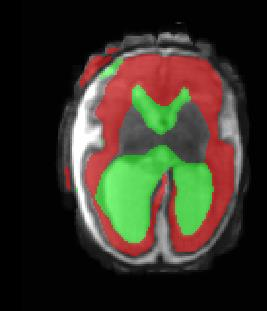
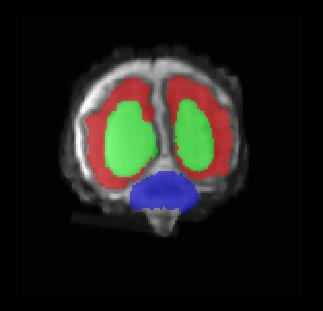
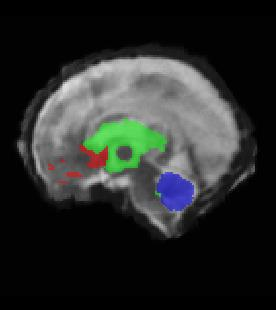
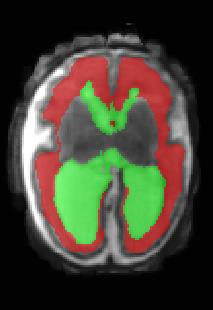
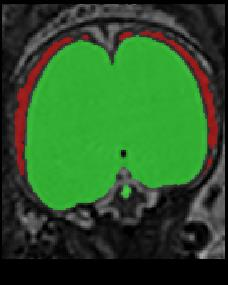
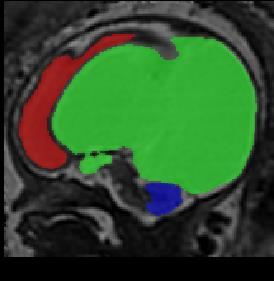
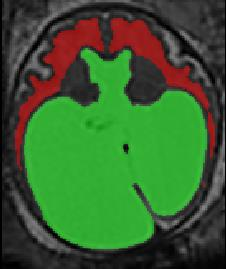
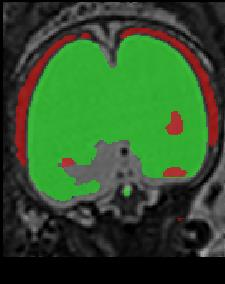
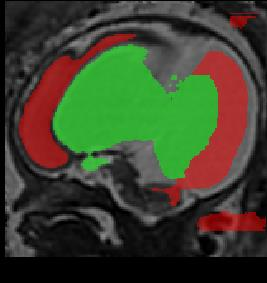
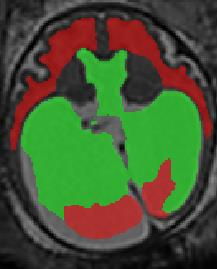
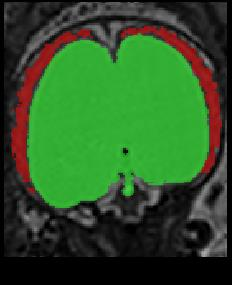
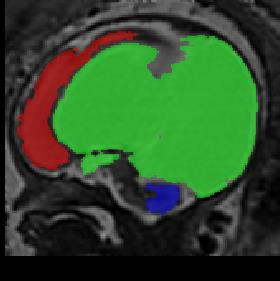
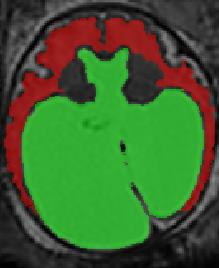
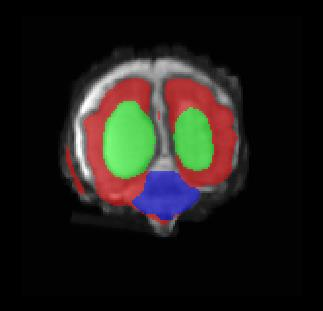
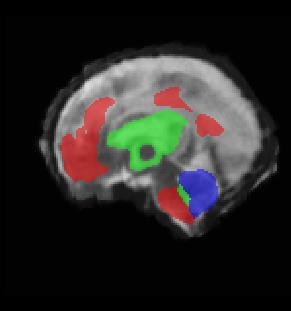
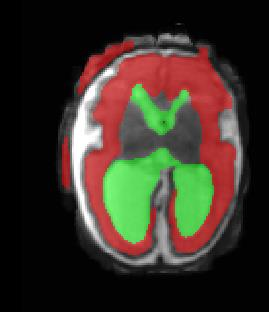
Limiting failures of machine learning systems is of paramount importance for safety-critical applications. In order to improve the robustness of machine learning systems, Distributionally Robust Optimization (DRO) has been proposed as a generalization of Empirical Risk Minimization (ERM). However, its use in deep learning has been severely restricted due to the relative inefficiency of the optimizers available for DRO in comparison to the wide-spread variants of Stochastic Gradient Descent (SGD) optimizers for ERM. We propose SGD with hardness weighted sampling, a principled and efficient optimization method for DRO in machine learning that is particularly suited in the context of deep learning. Similar to a hard example mining strategy in practice, the proposed algorithm is straightforward to implement and computationally as efficient as SGD-based optimizers used for deep learning, requiring minimal overhead computation. In contrast to typical ad hoc hard mining approaches, we prove the convergence of our DRO algorithm for over-parameterized deep learning networks with ReLU activation and a finite number of layers and parameters. Our experiments on fetal brain 3D MRI segmentation and brain tumor segmentation in MRI demonstrate the feasibility and the usefulness of our approach. Using our hardness weighted sampling for training a state-of-the-art deep learning pipeline leads to improved robustness to anatomical variabilities in automatic fetal brain 3D MRI segmentation using deep learning and to improved robustness to the image protocol variations in brain tumor segmentation. Our code is available at https://github.com/LucasFidon/HardnessWeightedSampler.
翻译:限制机器学习系统失灵对于机构风险管理至关重要。为了提高机器学习系统的稳健性,建议将分布式强力优化(DRO)作为 " 经验风险最小化(ERM) " 的概括性做法。然而,由于DRO可利用的优化优化器效率相对而言相对而言较低,因此在深层学习中的使用受到严重限制,因为DRO可利用的优化器与机构风险管理Stochatistic Gradient Erniversity(SGD)优化器的广泛变体相比效率相对较低。我们建议以硬度加权抽样抽样为SGD,这是在深层学习中特别适合的机器学习中DRO的有原则的高效优化方法。 类似于实践中的硬性采矿战略一样,拟议的算法非常直接,可以像SGD为深层学习所用的优化优化优化优化的S。 与典型的硬性硬性精度精度深层学习网络相比,我们用高度深度学习网络的算法与RELU激活和定数层和参数相融合。我们用FD 3DMRI断层和脑构造分析方法改进了我们的硬性、硬性磁性对磁性进行升级的学习。