Survey Data Integration for Distribution Function Estimation

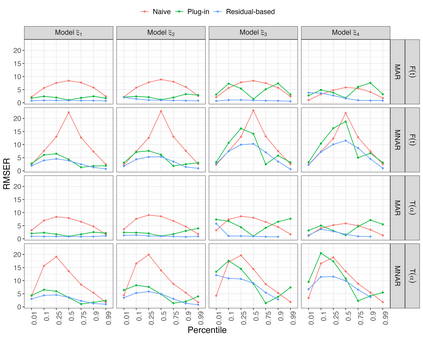
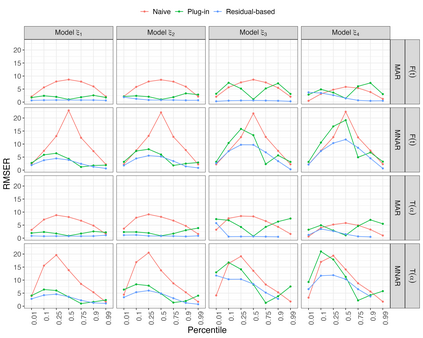
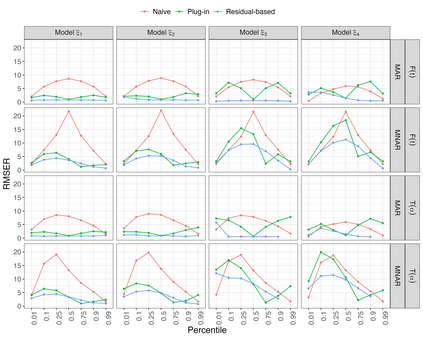
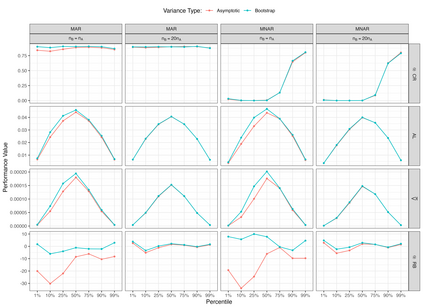
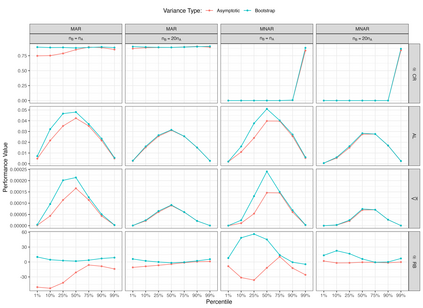
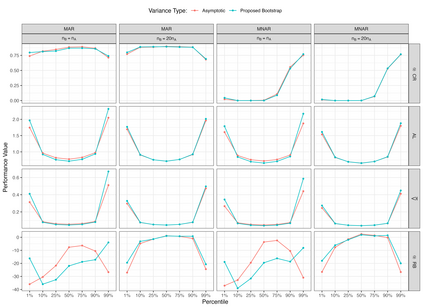
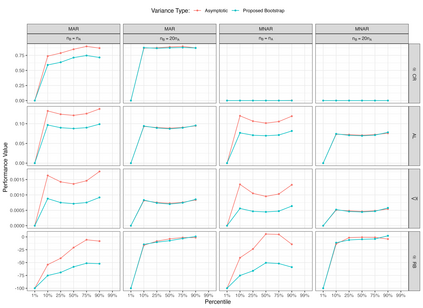
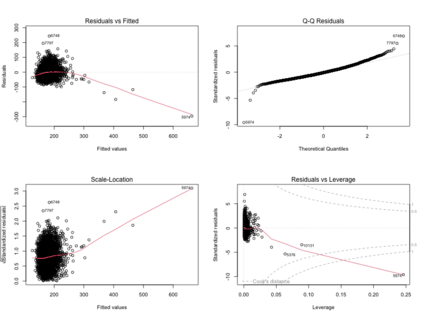
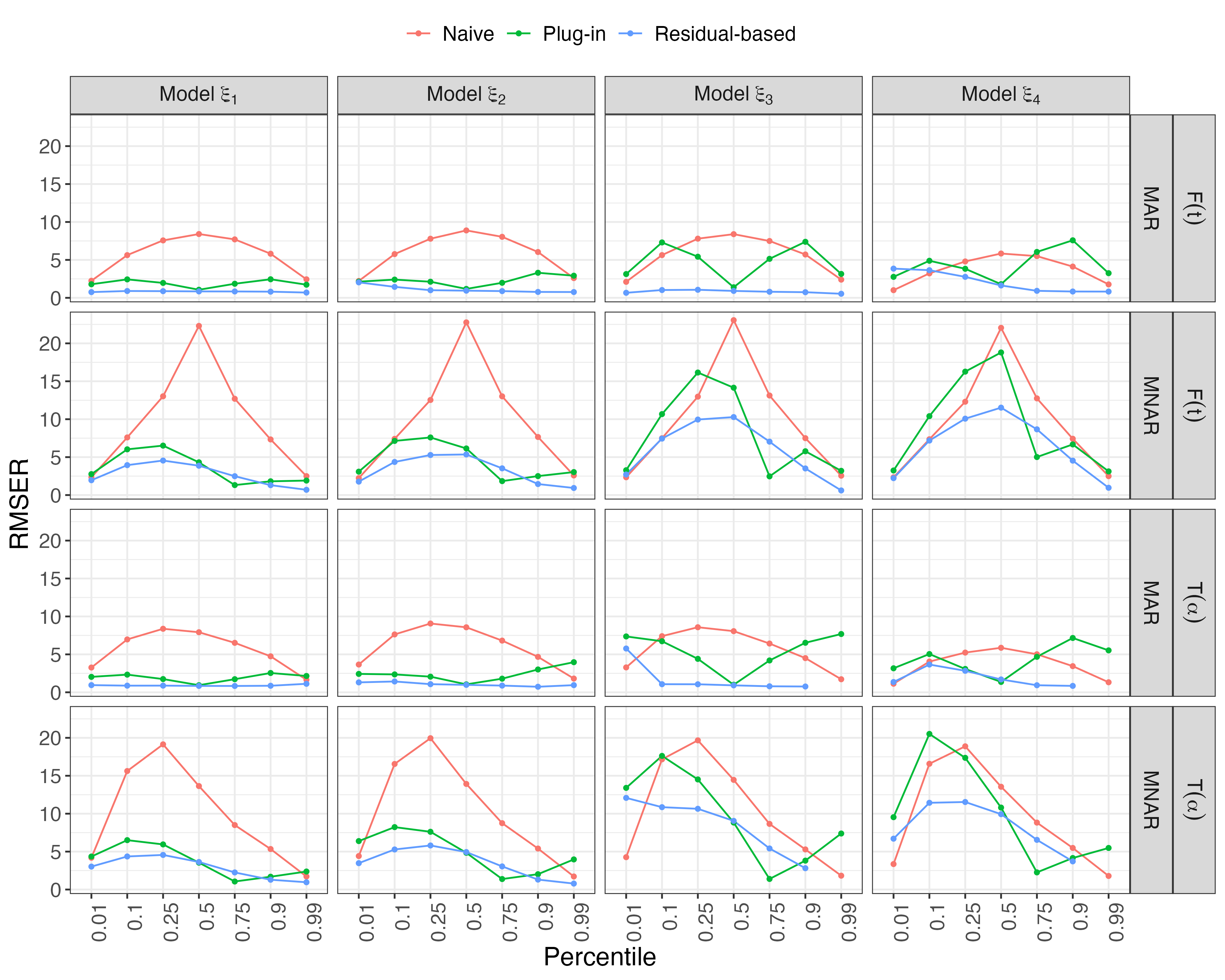
Estimates of finite population cumulativedistribution functions (CDFs) and quantiles are critical forpolicy-making, resource allocation, and public health planning. For instance, federal finance agencies may require accurate estimates of the proportion of individuals with income below the federal poverty line to determine funding eligibility, while health organizations may rely on precise quantile estimates of key health variables to guide local health interventions. Despite growing interest in survey data integration, research on the integration of probability and nonprobability samples toestimate CDFs and quantiles remains limited. In this study, we propose a novel residual-based CDF estimator that integrates information from a probability sample with data from potentially large nonprobability samples. Our approach leverages shared covariates observed in both datasets, while the response variable is available only in the nonprobability sample. Using a semiparametric approach, we train an outcome model on the nonprobability sample and incorporate model residuals with sampling weights from the probability sample to estimate the CDF of the target variable. Based on this CDF estimator, we define a quantile estimator and introduce linearization and bootstrap methods for variance estimation of both the CDF and quantile estimators. Under certain regularity conditions, we establish the asymptotic properties, including bias and variance, of the CDF estimator. Our empirical findings support the theoretical results and demonstrate the favorable performance of the proposed estimators relative to plug-in mass imputation estimators and the na\"ive estimators derived from the nonprobability sample only. A real data example is presented to illustrate the proposed estimators.