Towards Certified Robustness of Metric Learning

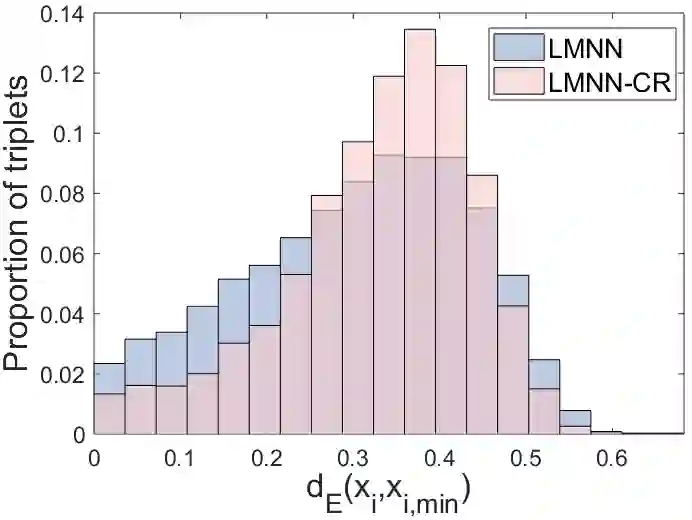
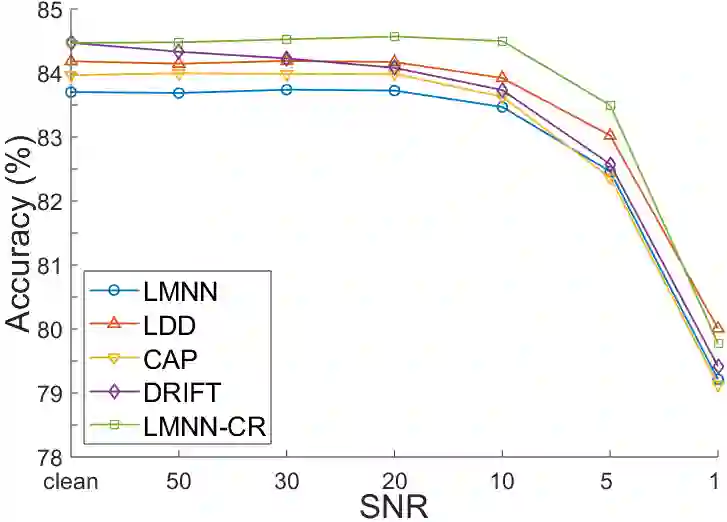
Metric learning aims to learn a distance metric such that semantically similar instances are pulled together while dissimilar instances are pushed away. Many existing methods consider maximizing or at least constraining a distance "margin" that separates similar and dissimilar pairs of instances to guarantee their performance on a subsequent k-nearest neighbor classifier. However, such a margin in the feature space does not necessarily lead to robustness certification or even anticipated generalization advantage, since a small perturbation of test instance in the instance space could still potentially alter the model prediction. To address this problem, we advocate penalizing small distance between training instances and their nearest adversarial examples, and we show that the resulting new approach to metric learning enjoys a larger certified neighborhood with theoretical performance guarantee. Moreover, drawing on an intuitive geometric insight, the proposed new loss term permits an analytically elegant closed-form solution and offers great flexibility in leveraging it jointly with existing metric learning methods. Extensive experiments demonstrate the superiority of the proposed method over the state-of-the-arts in terms of both discrimination accuracy and robustness to noise.