读论文Discriminative Deep Metric Learning for Face and KV

这篇文章是发表在TIP2017上的一篇关于人脸识别和亲属识别的一篇文章，作者是清华大学鲁继文他们团队关于深度度量学习的一篇新作。

该论文主要是在度量学习的基础上利用神将网络实现的，解决类内距离尽可能小，类间距离尽可能大的问题。创新点在于提出了两个神经网络的框架discriminative deep metric learning (DDML)以及discriminativedeep multi metric learning (DDMML)，DDML框架主要是用来通过全连接的神经网络进行度量学习，通过最后的损失函数保证类内距离小，类间距离大。而DDMML框架主要也是利用度量学习的思想将多个低层人工设计的特征有效融合起来，实现类内差异性小于类间差异性的问题。二者都是利用度量学习的思想，但是度量学习只是对原始的特征做线性转换，不符合人脸位于高维流行域上的几何分布，通过神经网络可以方便的实现对特征的高维非线性映射，使学到的特征更具有判别性，更有利于分类。接下来我们看看具体是怎么实现的。

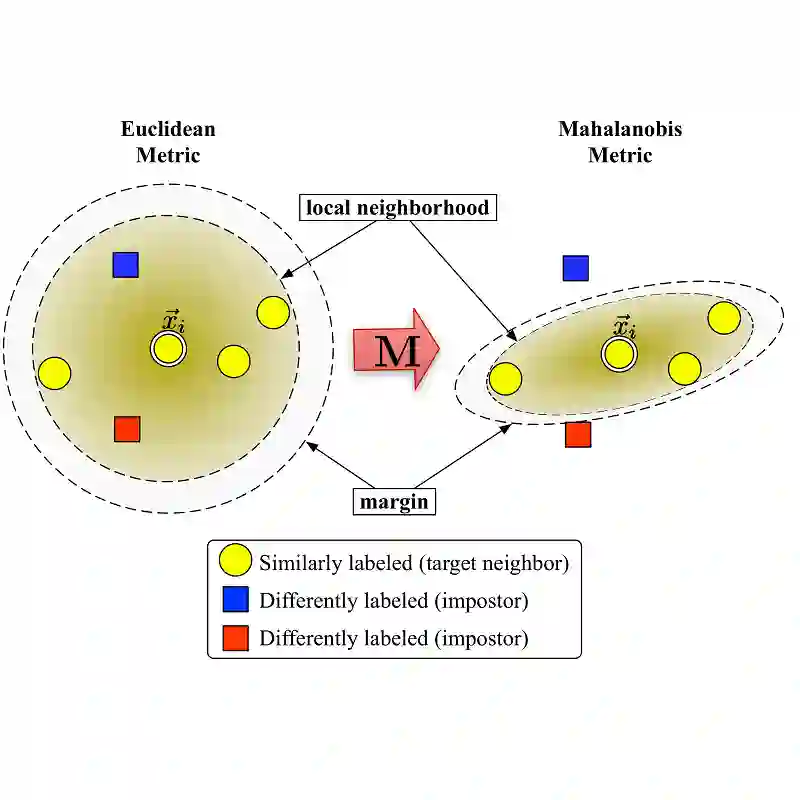
首先我们先回顾一下度量学习的基础知识，度量学习是为了让没有亲属关系的样本距离尽可能的远，而具有亲属关系的样本距离尽可能的近，使得原始空间中的马氏距离等价于转换空间后的欧氏距离。

接下来我们看一下本论文提出的第一种模型-DDML，整个算法的框架如下:

通过多个隐含层单元的计算，第一层的输出最终神经网络的输出为输入两幅图像的相似性通过欧式距离计算，即，基于度量学习的思想，整个网络的目标就是寻找一个合适的非线性映射函数f使得正样本对之间的距离小于一个很小的值t1(t1>0),负样本对之间的距离大于一个大的值t2（t2>t1）。本文中，为了减少参数的数量，作者将t1与t2进行了融合只使用了一个参数t（t>1）来保证这种约束的实现，即其中t1=t-1,t2=t+1,lij表示两个样本之间的相似性，如果两个样本属于同一类，则lij=1，否则lij=-1。此时的优化问题变成了：

以上公式通过随机梯度下降可以进行求解优化。

接下来我们看一下第二种模型-DDMML,算法流程图如下：

此时的优化问题变成了

同样通过随机梯度下降可以进行求解，具体实现细节可以参考论文。

最后，作者在多个数据集上做了对比实验证明了模型的优越性。人脸识别：

亲属识别：