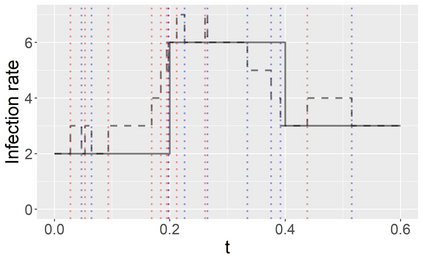
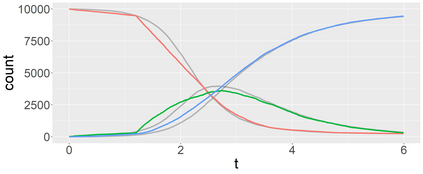
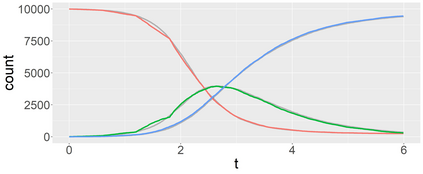
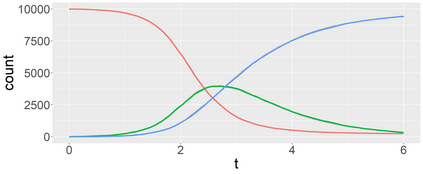
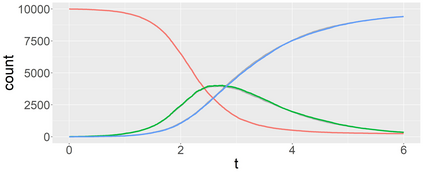
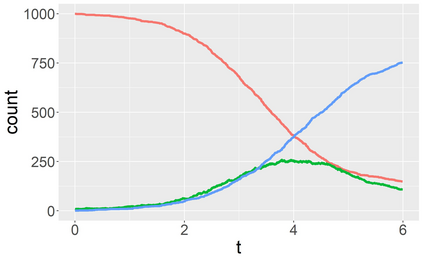
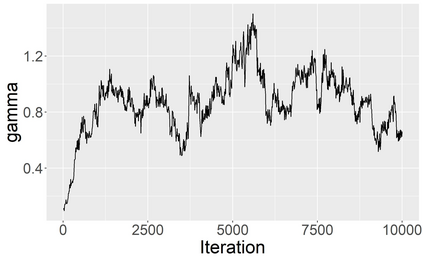
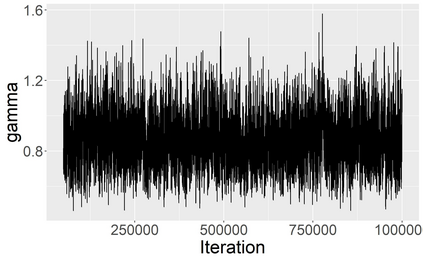
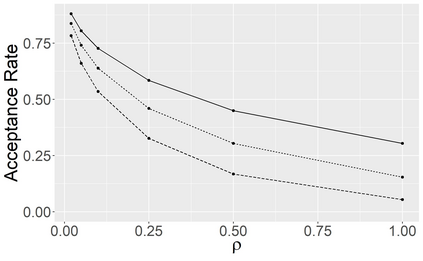
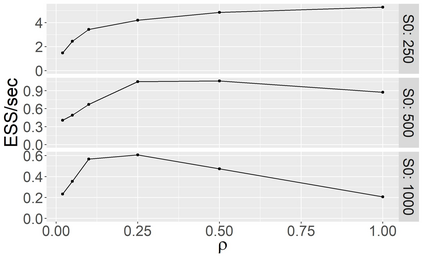
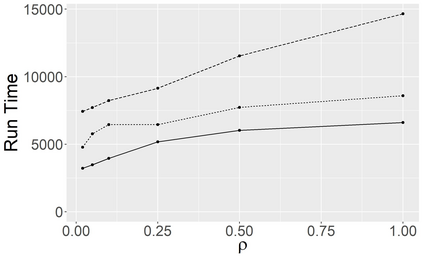
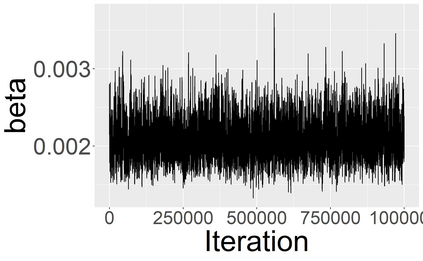
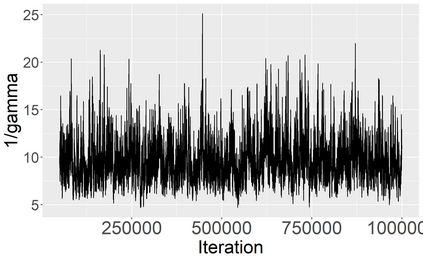
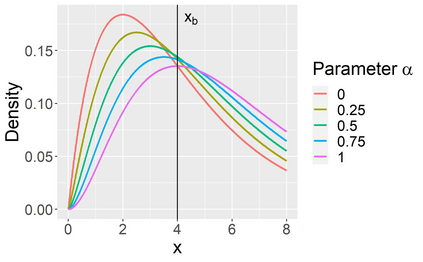
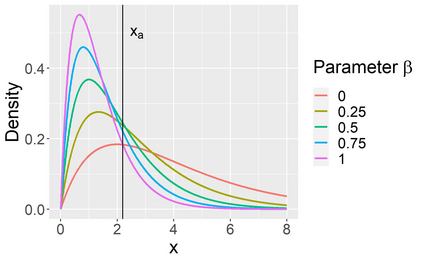
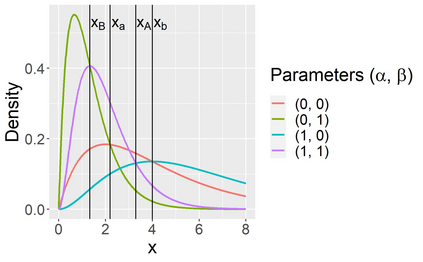
Stochastic epidemic models provide an interpretable probabilistic description of the spread of a disease through a population. Yet, fitting these models when the epidemic process is only partially observed is a notoriously difficult task due to the intractability of the likelihood for many classical models. To remedy this issue, this article introduces a novel data-augmented MCMC algorithm for fast and exact Bayesian inference for the stochastic SIR model given discretely observed infection incidence counts. In a Metropolis-Hastings step, new event times of the latent data are jointly proposed from a surrogate process that closely resembles the SIR, and from which we can efficiently generate epidemics compatible with the observed data. The proposed DA-MCMC algorithm is fast and, since the latent data are generated from a faithful approximation of the target model, a large portion thereof can be updated per iteration without prohibitively lowering the acceptance rate. We find that the method explores the high-dimensional latent space efficiently and scales to outbreaks with hundreds of thousands of individuals, and we show that the Markov chain underlying the algorithm is uniformly ergodic. We validate its performance via thorough simulation experiments and a case study on the 2013-2015 Ebola outbreak in Western Africa.
翻译:斯托氏流行病模型对疾病在人群中的传播提供了可解释的概率描述。然而,由于许多古典模型的可能性难以接受,因此,在仅部分观察到流行病过程只是部分被观察到时安装这些模型是一项臭名昭著的困难任务,因为许多古典模型可能难以吸引。为解决这个问题,本文章引入了一种新的数据强化MCMC算法,用于快速和精确的巴伊西亚测序,根据不连续观测到的感染发生率,对随机SIR模型进行快速和精确的贝叶色推论。在大都会-哈斯阶段,从一个与SIR非常相似的代孕过程联合提出了潜在数据的新事件次数,从中我们可以有效地产生与所观察到的数据相容的流行病。提议的DA-MC算法是快速的,由于潜在数据来自目标模型的忠实近似近,因此大部分数据可以随其反复更新,而不会令人望目惊心动地降低接受率。我们发现,该方法探索高度的潜伏空间和尺度,可以与数十万人一起爆发,我们展示2013年马可用作算法基础的链,以便有效地产生与所观察到的流行病的流行病。我们通过彻底的中东的试验来验证。