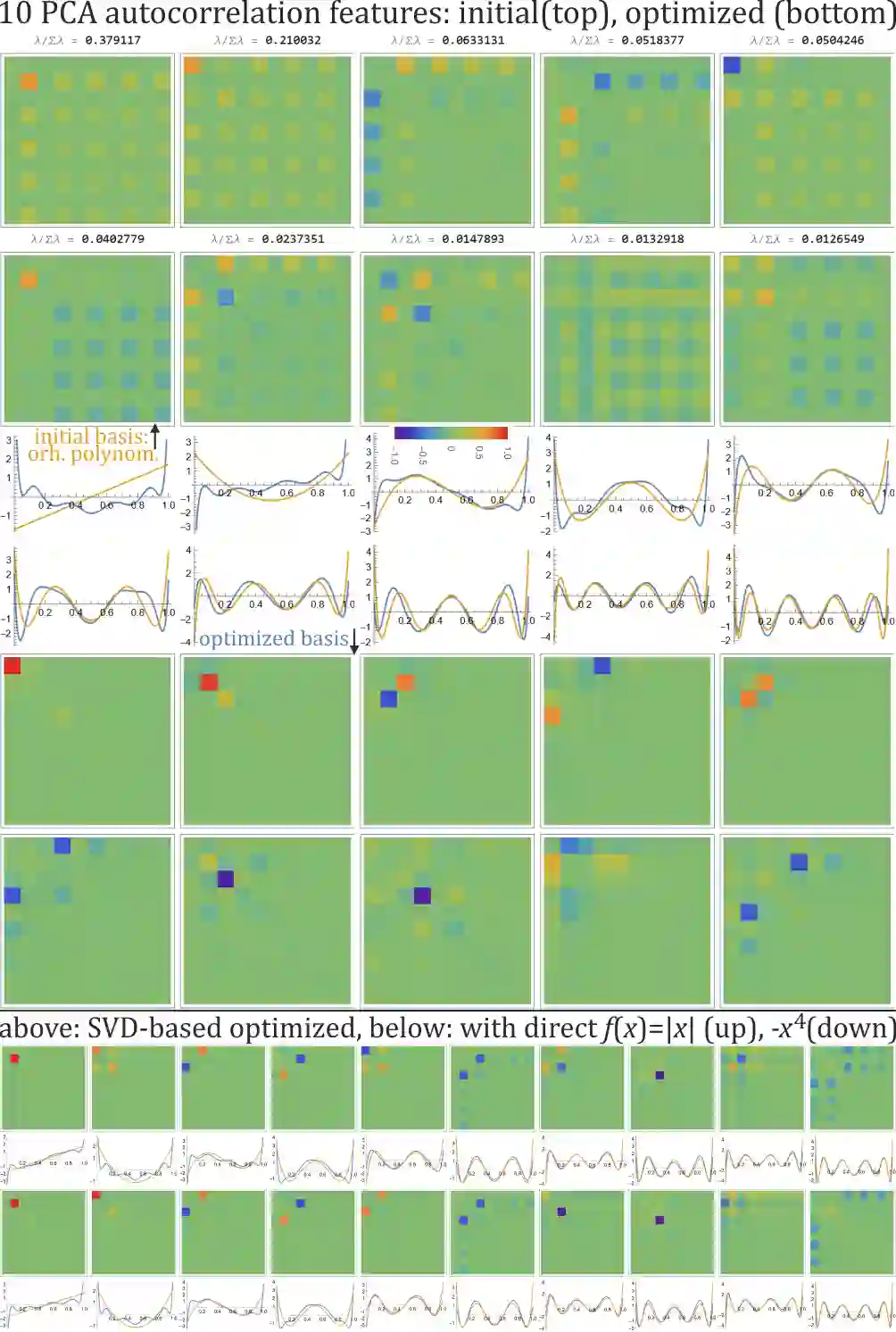
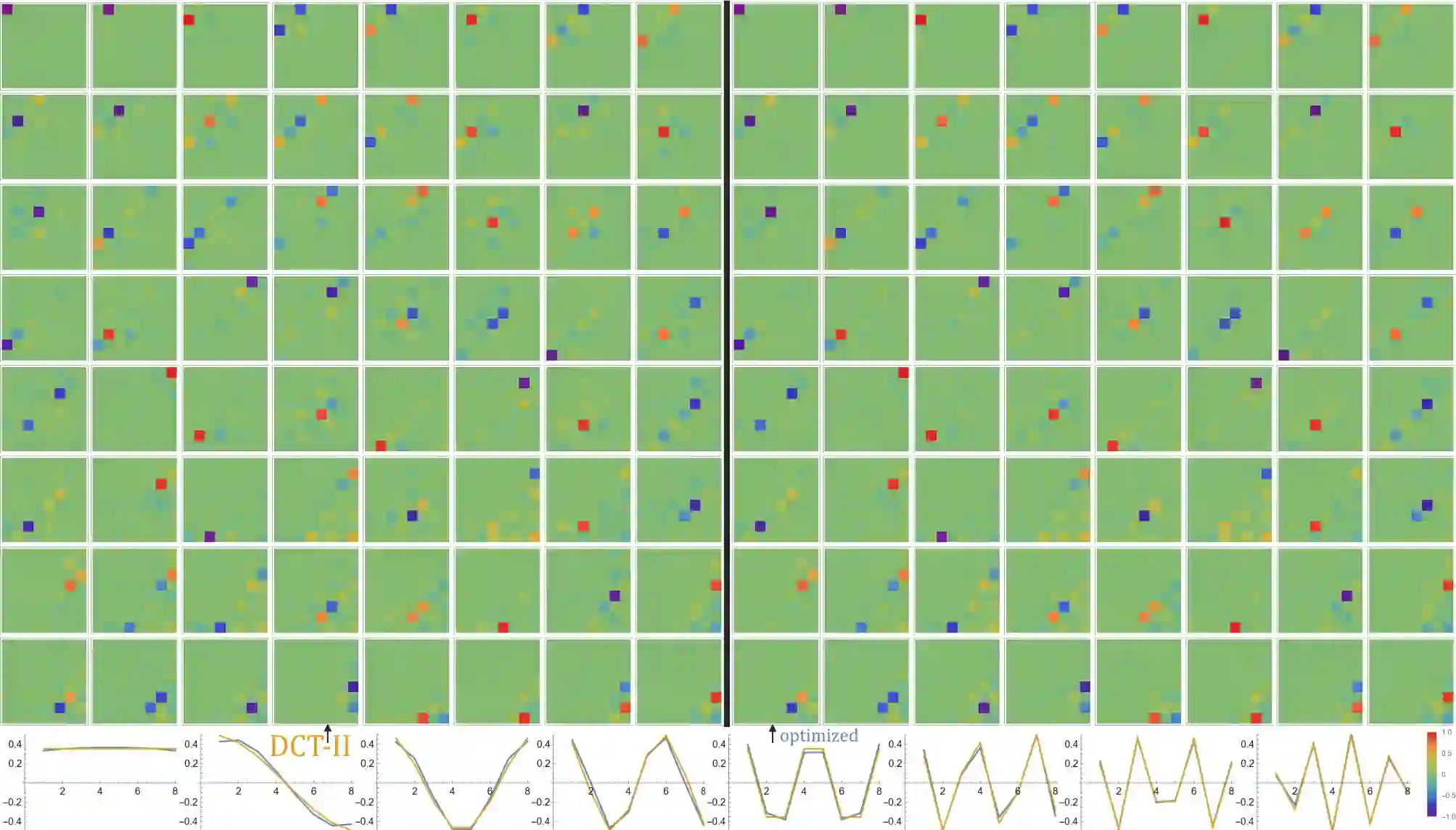
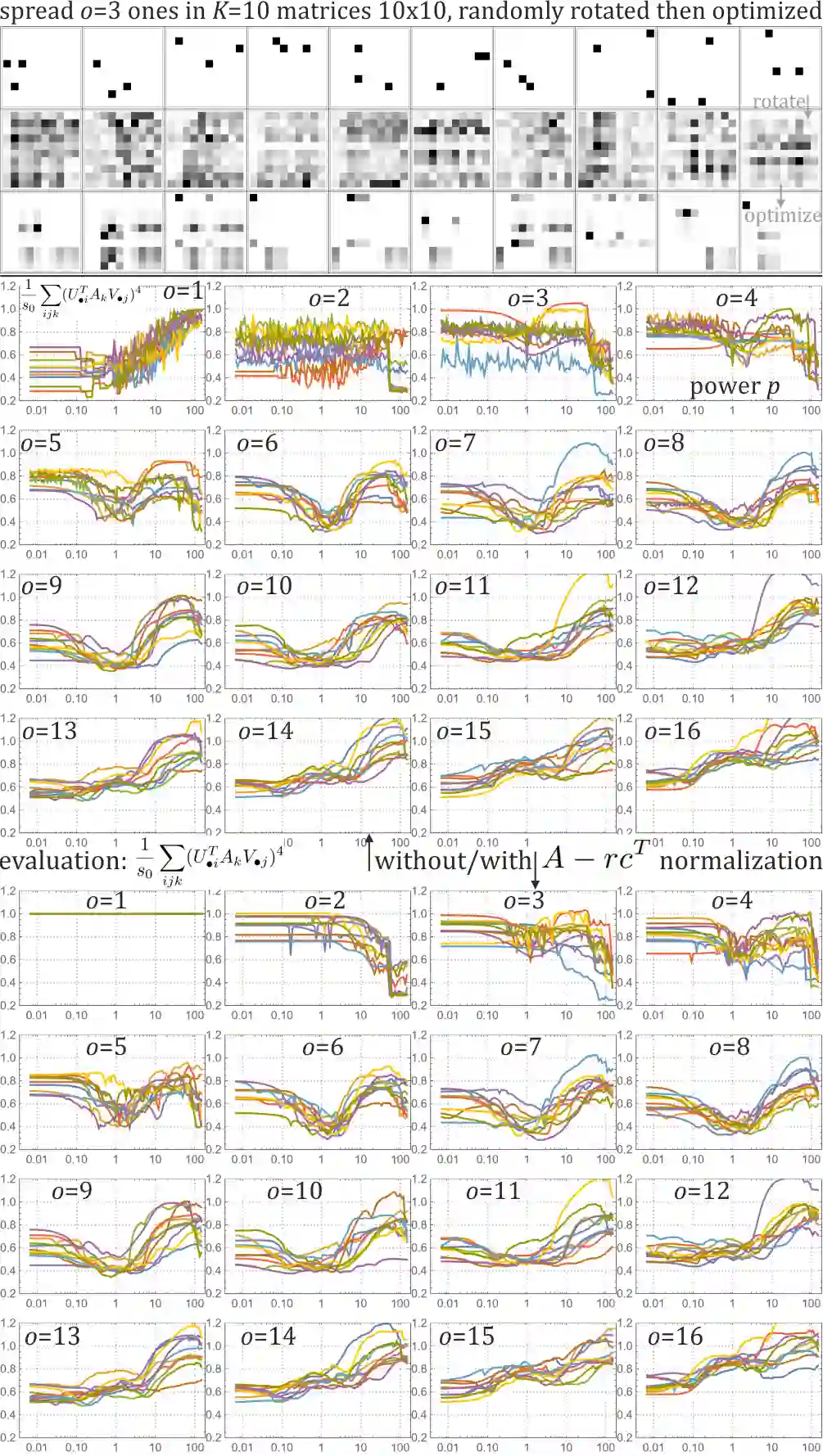
SVD (singular value decomposition) is one of the basic tools of machine learning, allowing to optimize basis for a given matrix. However, sometimes we have a set of matrices $\{A_k\}_k$ instead, and would like to optimize a single common basis for them: find orthogonal matrices $U$, $V$, such that $\{U^T A_k V\}$ set of matrices is somehow simpler. For example DCT-II is orthonormal basis of functions commonly used in image/video compression - as discussed here, this kind of basis can be quickly automatically optimized for a given dataset. While also discussed gradient descent optimization might be computationally costly, there is proposed CSVD (common SVD): fast general approach based on SVD. Specifically, we choose $U$ as built of eigenvectors of $\sum_i (w_k)^q (A_k A_k^T)^p$ and $V$ of $\sum_k (w_k)^q (A_k^T A_k)^p$, where $w_k$ are their weights, $p,q>0$ are some chosen powers e.g. 1/2, optionally with normalization e.g. $A \to A - rc^T$ where $r_i=\sum_j A_{ij}, c_j =\sum_i A_{ij}$.
翻译:SVD( 星值分解) 是机器学习的基本工具之一, 可以优化给定矩阵的基础。 但是, 有时我们拥有一套基质 $ {A_ k ⁇ k$, 代之以, 并且想要优化一个单一的共同基础 : 找到正方基质 $U$, 美元, 也就是说, 美元是比较简单的 。 例如, DCT- II 是图像/ 视频压缩中常用函数的正态基础 - 正如这里所讨论的那样, 这种基点可以快速为给定数据集自动优化 。 虽然我们讨论的梯度下降优化可能具有计算成本 : 在 SVD 的基础上, 我们选择快速的通用方法 。 具体地说, 我们选择的美元是 $_ sum_ (wk) q (A_ k A_ k_ k$) 和 $\ sum_ k} (w_ k) 美元 ( e_ k) (A_ k_ t_ x_ 美元) 美元 和 A_ k_ r_ r_ a_ t_ r_ r_ t_ ab) r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ rx, 这里选择 r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_ r_