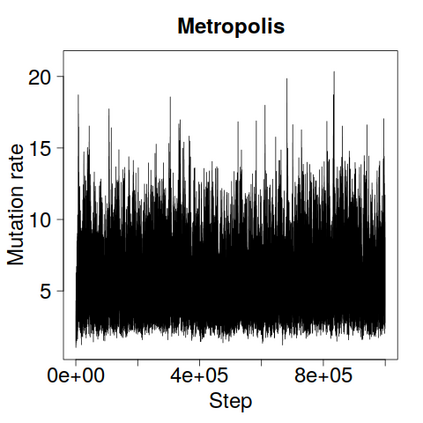
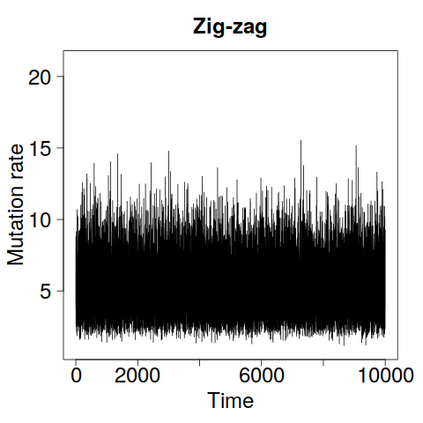
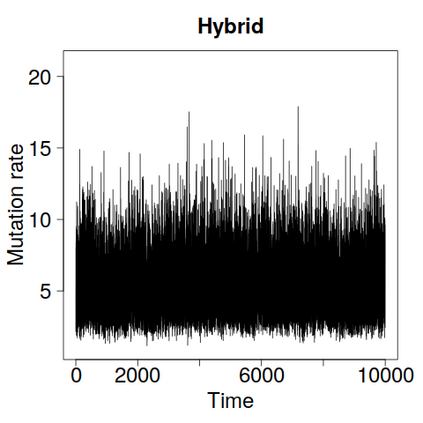
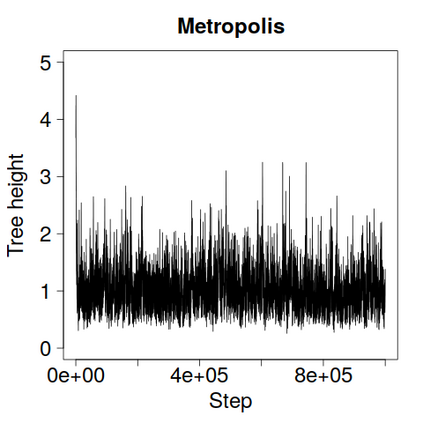
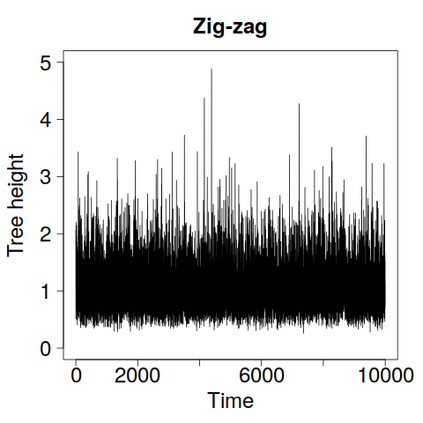
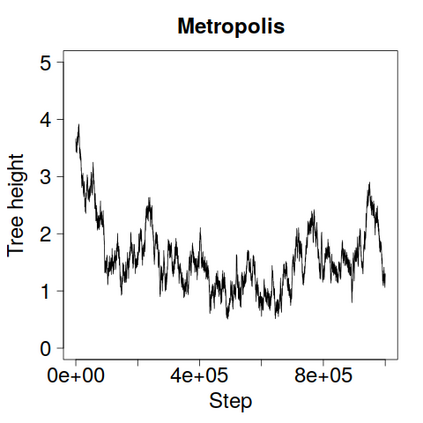
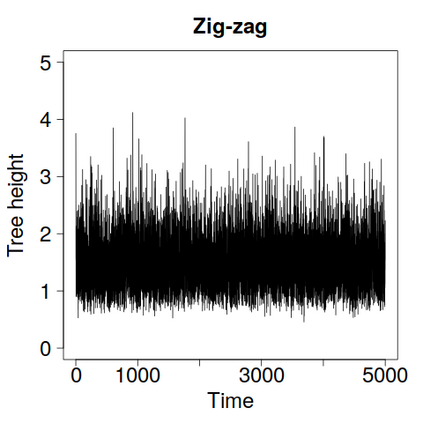
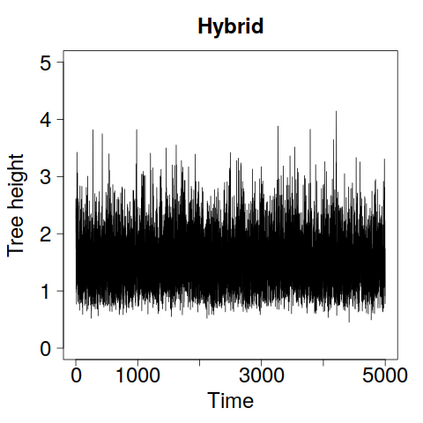
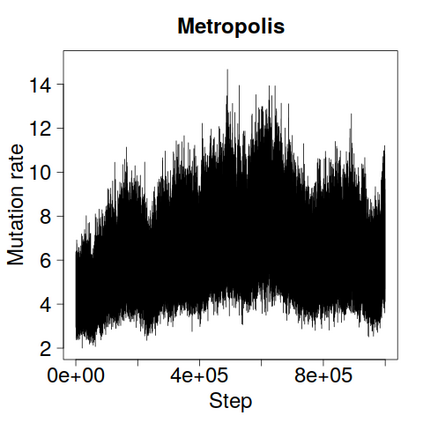
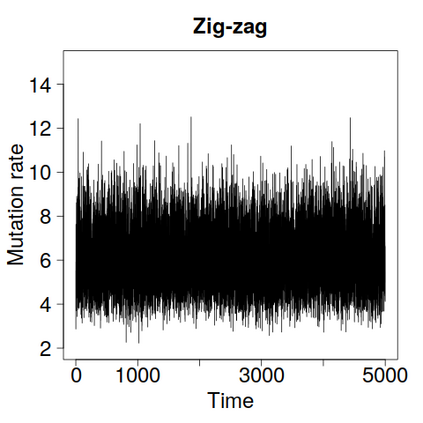
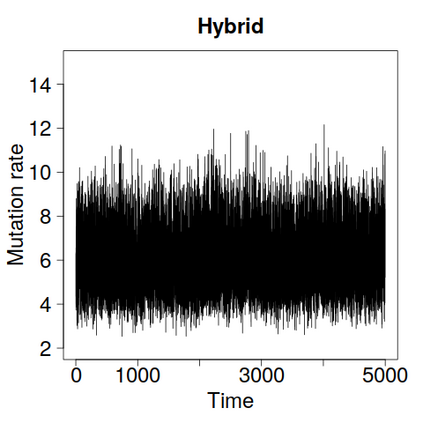
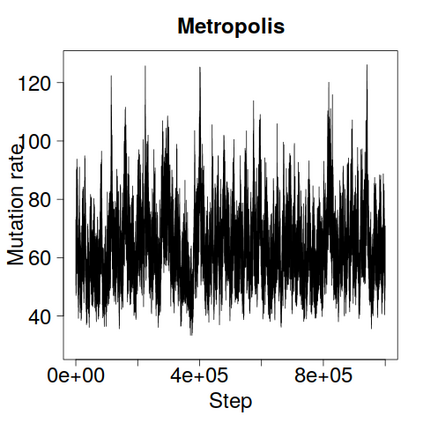
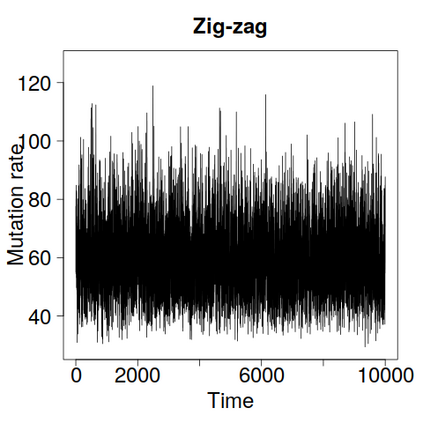
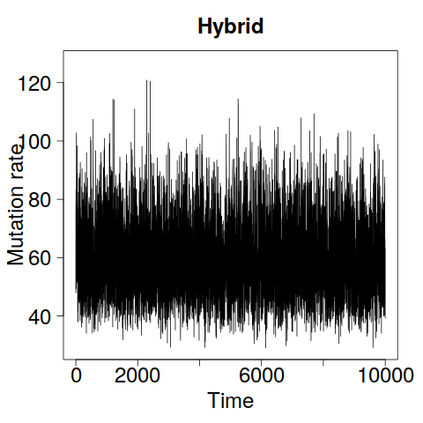
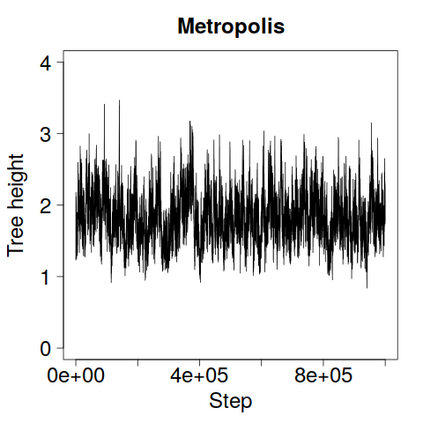
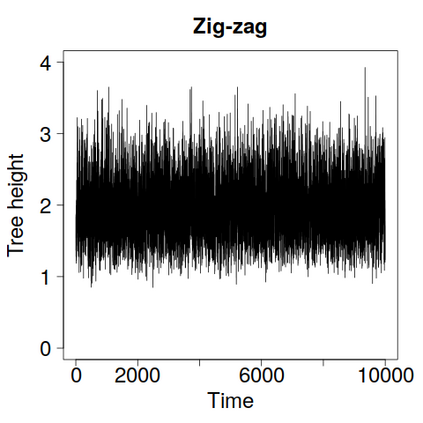
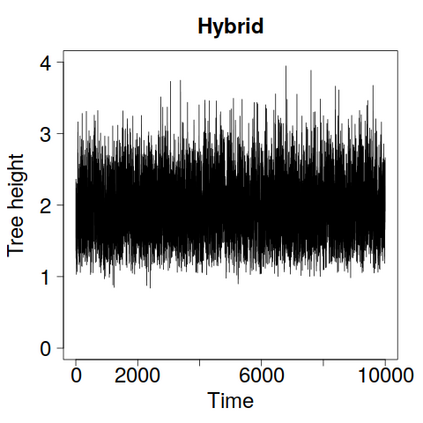
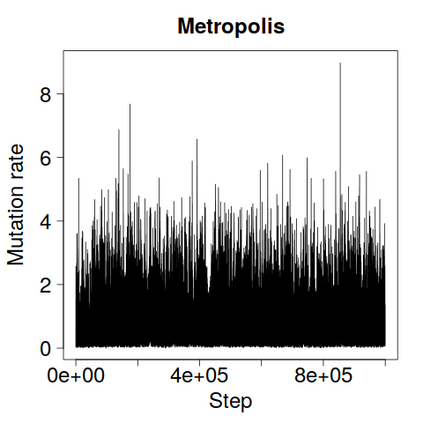
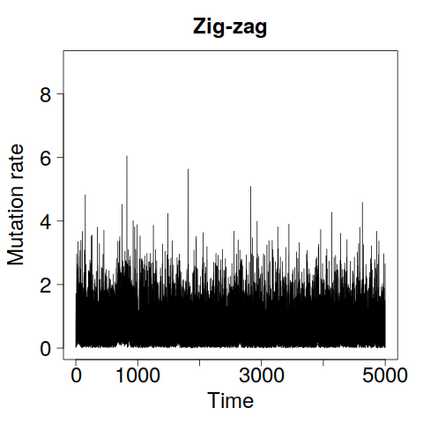
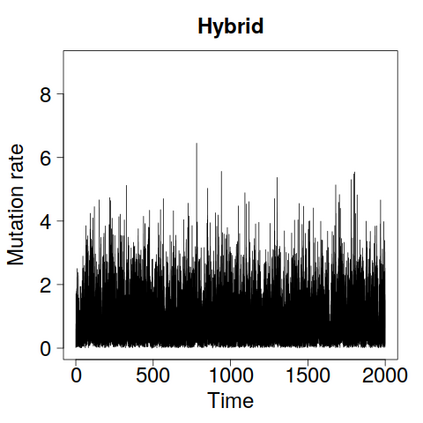
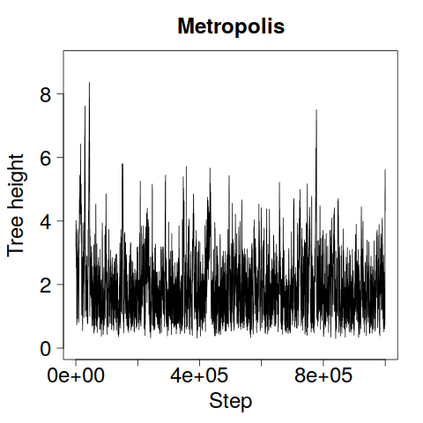
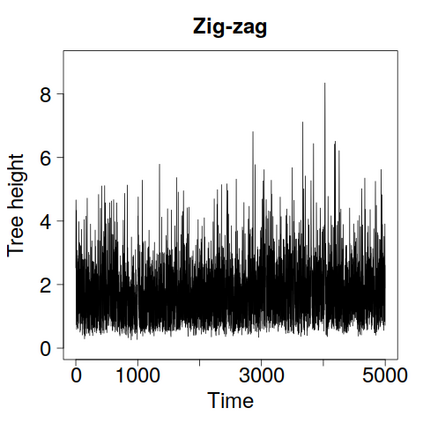
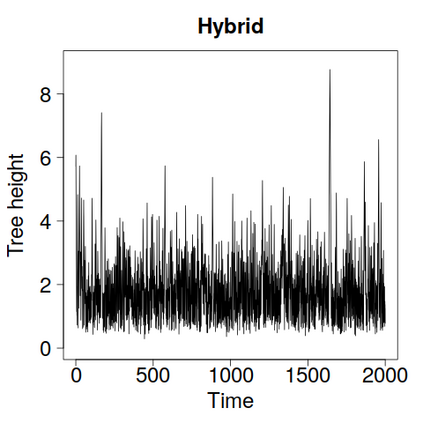
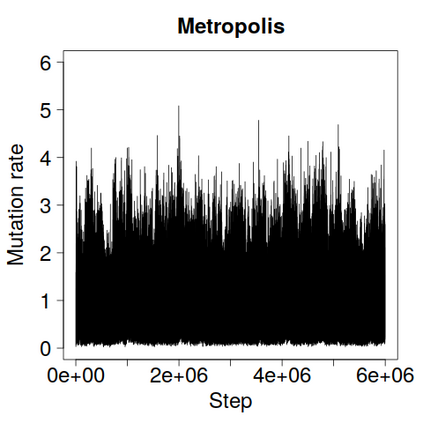
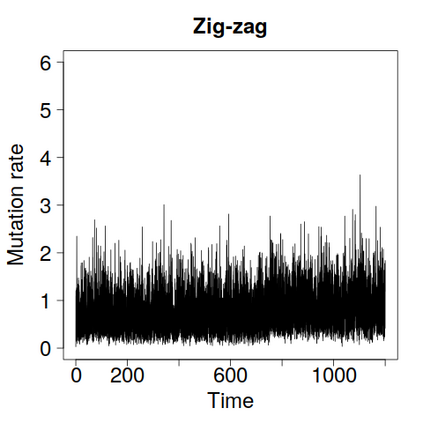
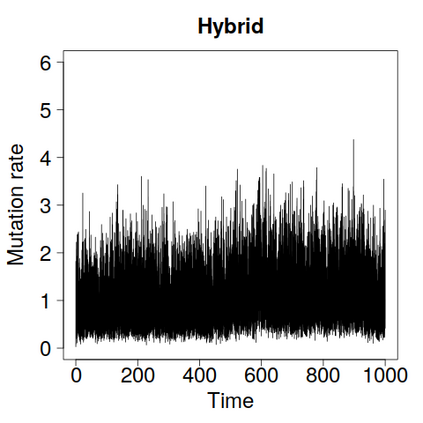
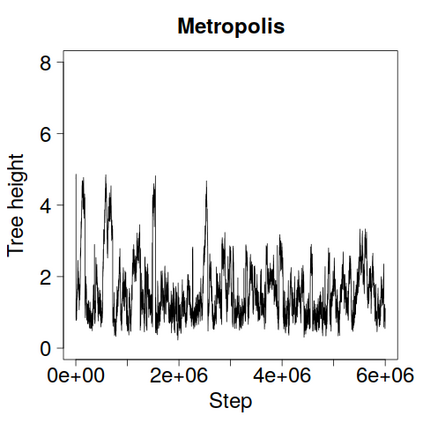
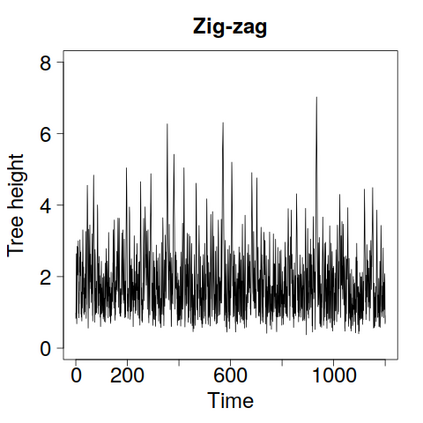
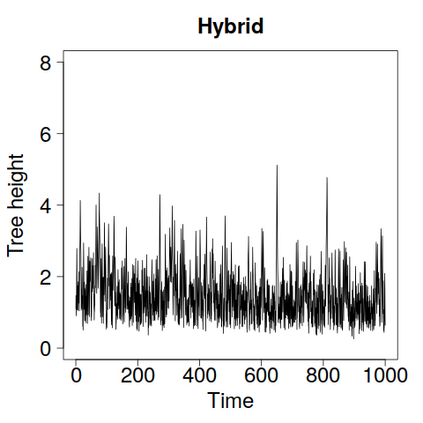
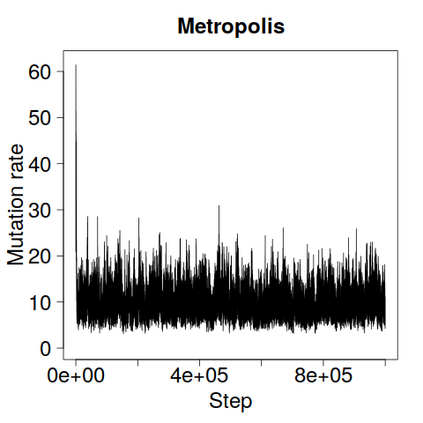
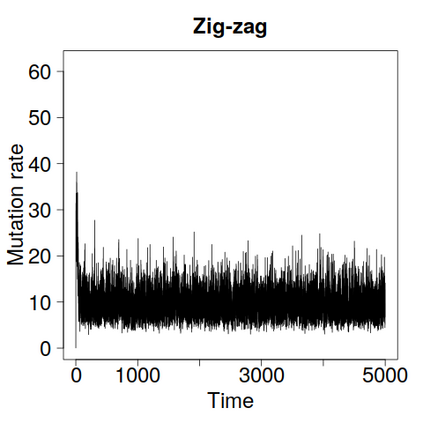
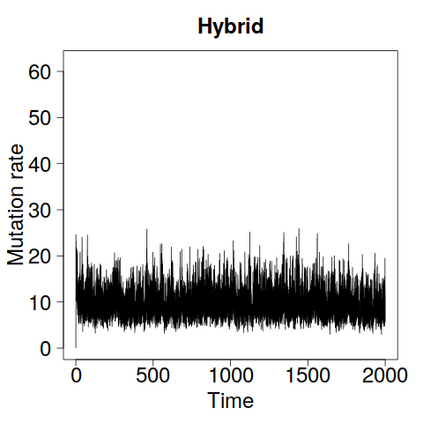
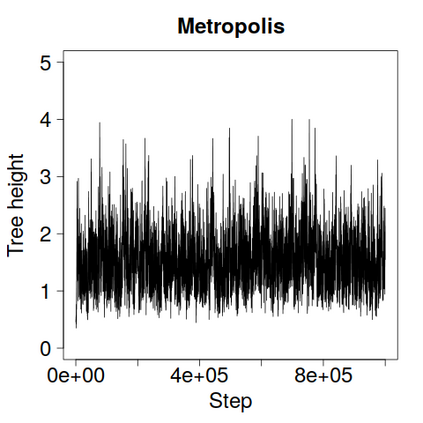
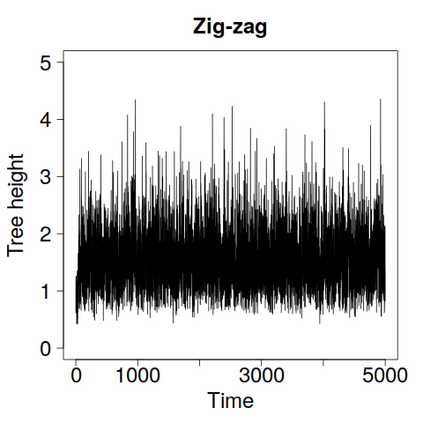
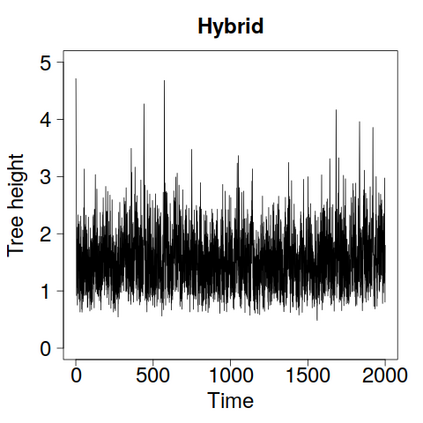
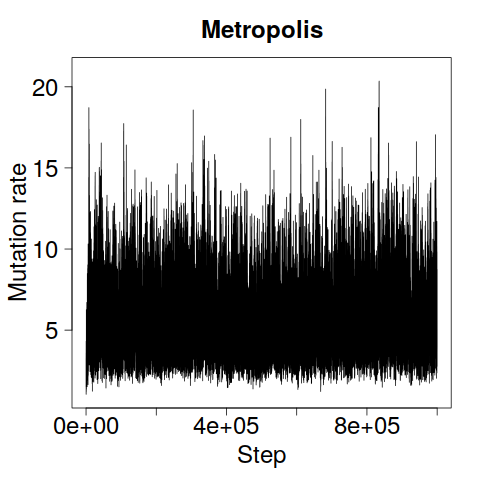
We construct a zig-zag process targeting a posterior distribution defined on a hybrid state space consisting of both discrete and continuous variables. The construction does not require any assumptions on the structure among discrete variables. We demonstrate our method on two examples in genetics based on the Kingman coalescent, showing that the zig-zag process can lead to efficiency gains of up to several orders of magnitude over classical Metropolis-Hastings algorithms, and that it is well suited to parallel computation. Our construction resembles existing techniques for Hamiltonian Monte Carlo on a hybrid state space, which suffers from implementationally and analytically complex boundary crossings when applied to the coalescent. We demonstrate that the continuous-time zig-zag process avoids these complications.
翻译:我们针对由离散变量和连续变量组成的混合状态空间定义的后方分布,构建一个zig-zag进程。建设不需要对离散变量的结构作任何假设。我们用基于Kingman型煤炭的遗传学的两个实例展示了我们的方法,表明zig-zag进程可以带来效率收益,超过传统的大都会-哈斯廷斯算法的多个数量级,而且它非常适合平行计算。我们的构建类似于汉密尔顿-蒙特-卡洛在混合状态空间上的现有技术,该混合状态空间在应用到煤炭时代时,因执行和分析上复杂的边界过境点而受到影响。我们证明连续时间的zig-zag进程可以避免这些复杂问题。