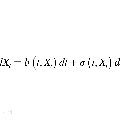Exponential superiority in probability of stochastic symplectic methods for linear stochastic oscillator

This paper proposes a novel concept of exponential superiority in probability to compare the numerical methods for general stochastic differential equations from the perspective of the tail probability of the error. We take the linear stochastic oscillator as the test equation and consider several concrete numerical methods. By establishing the large deviation principles of the errors of the considered numerical methods, we show that the symplectic methods are exponentially superior to the non-symplectic methods in probability when the computational time $T$ is sufficiently large. This provides a new way to explain the superiority of stochastic symplectic methods over non-symplectic methods in the long-time simulation.