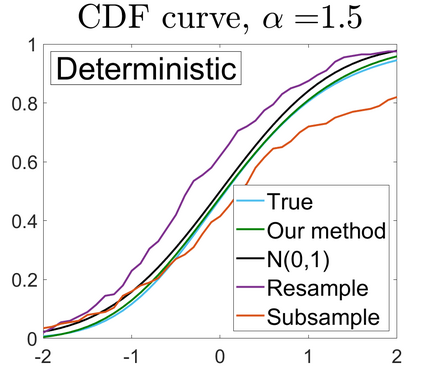
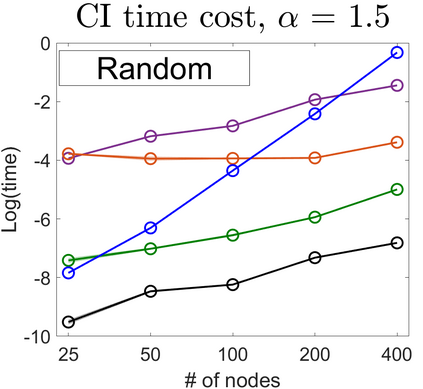
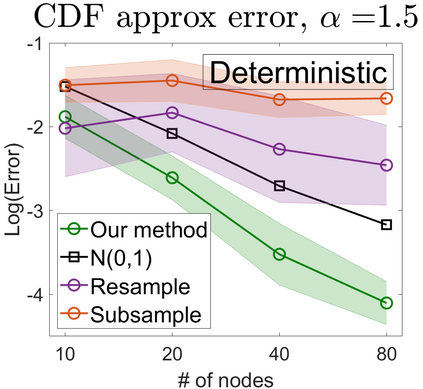
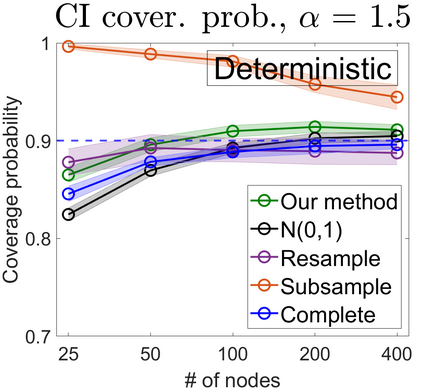
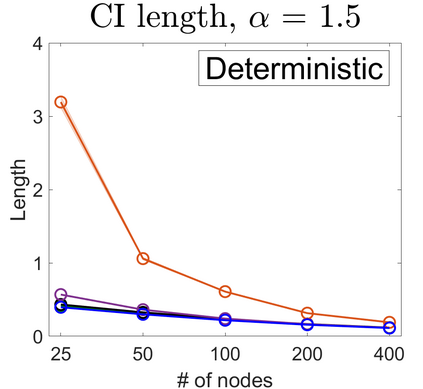
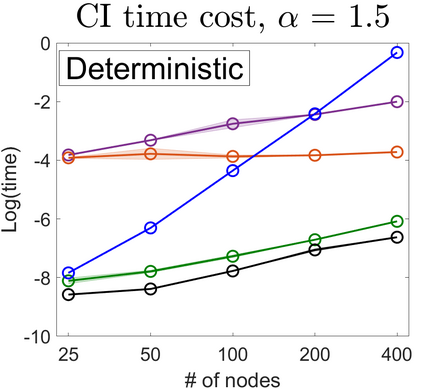
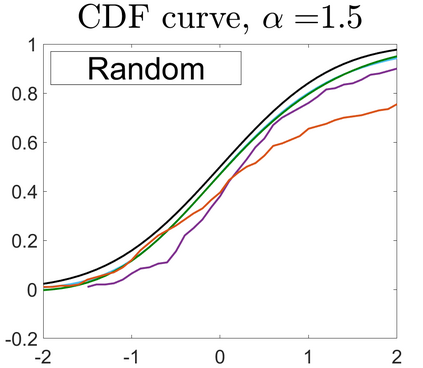
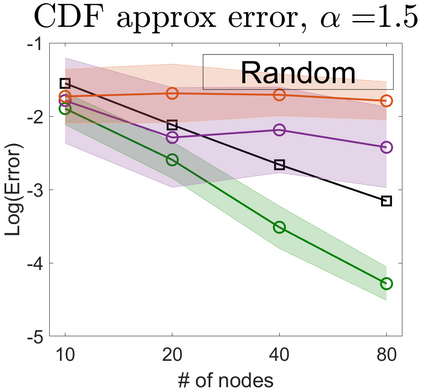
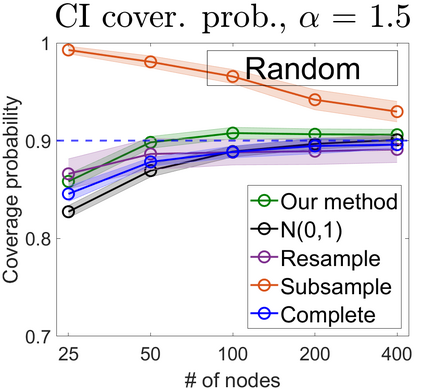
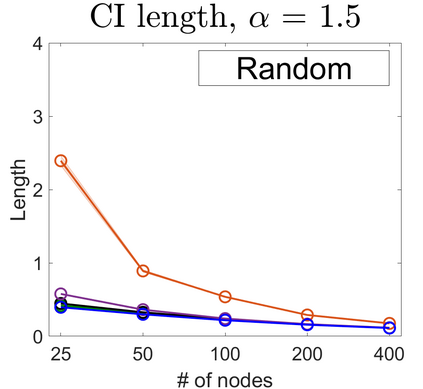
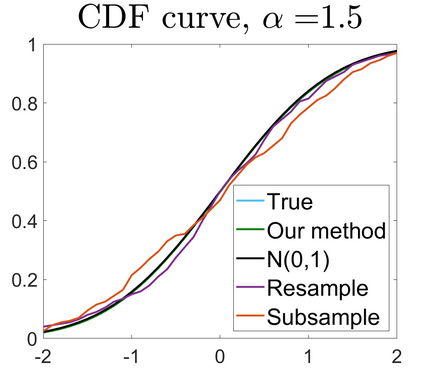
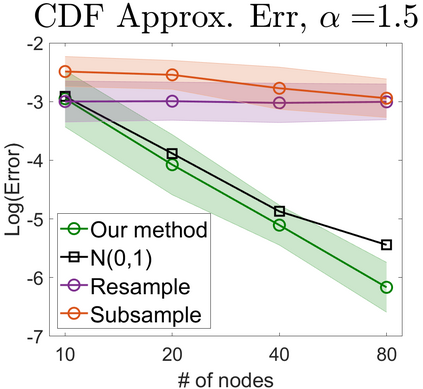
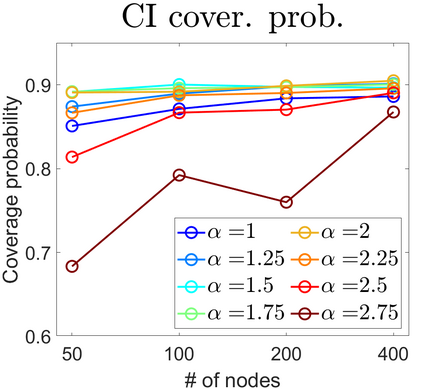
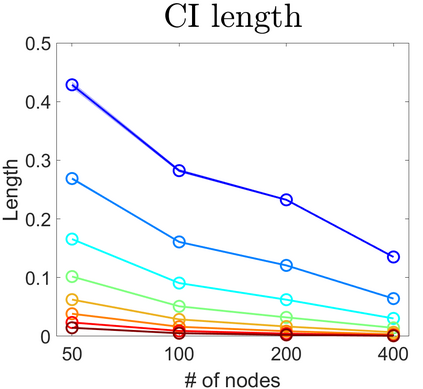
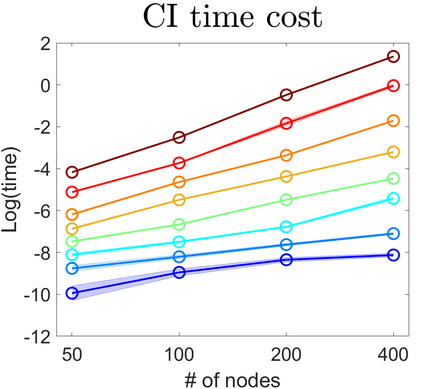
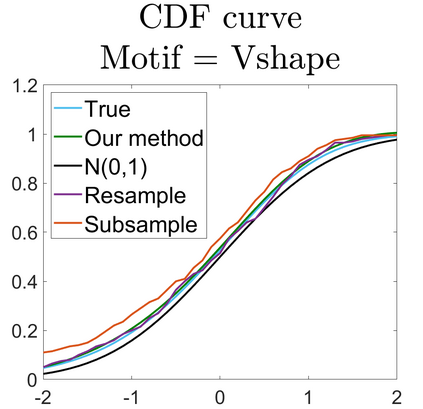
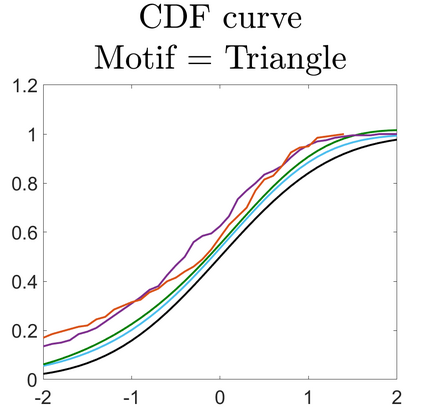
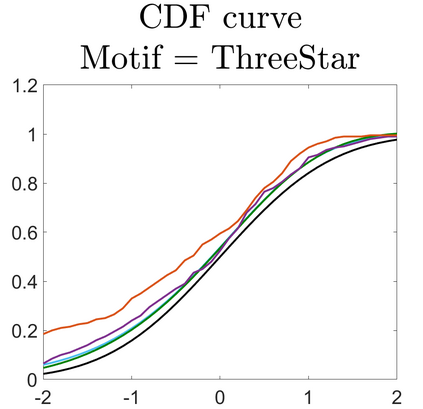
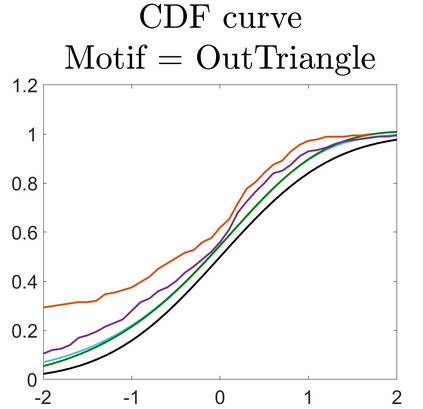
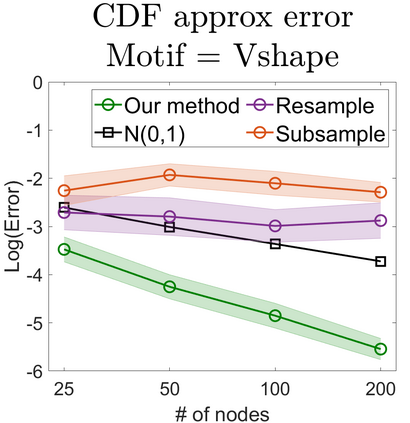
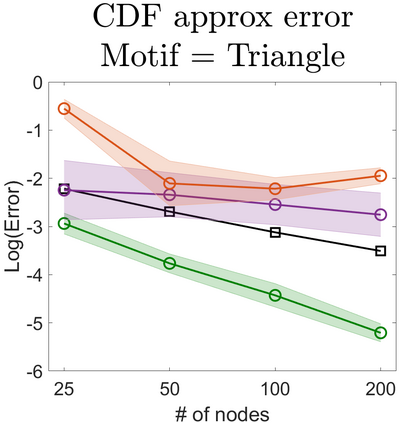
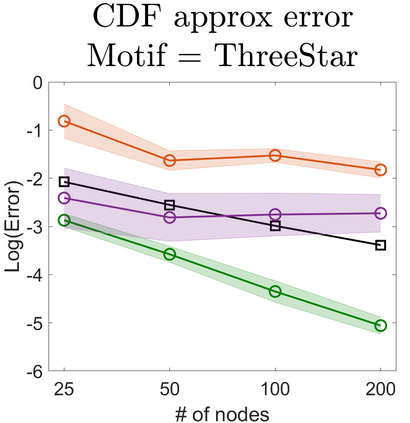
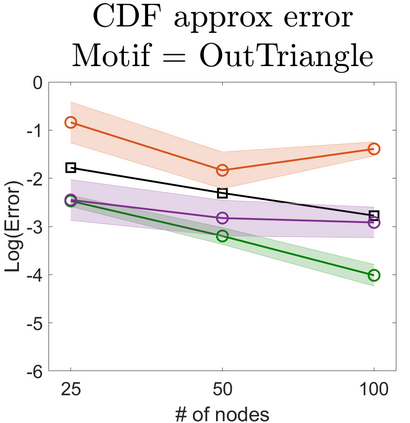
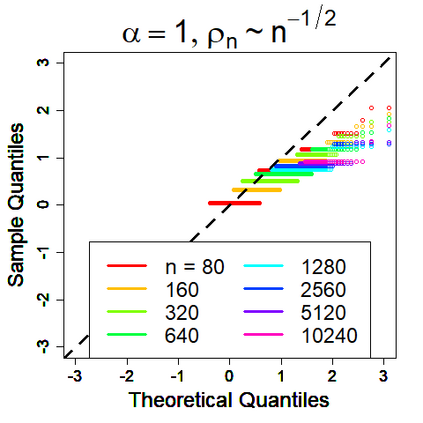
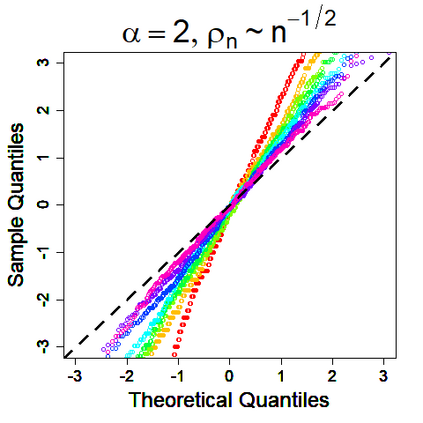
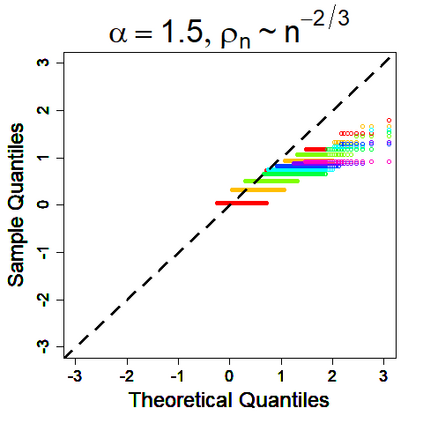
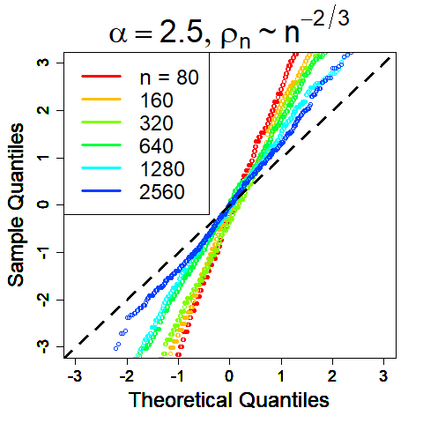
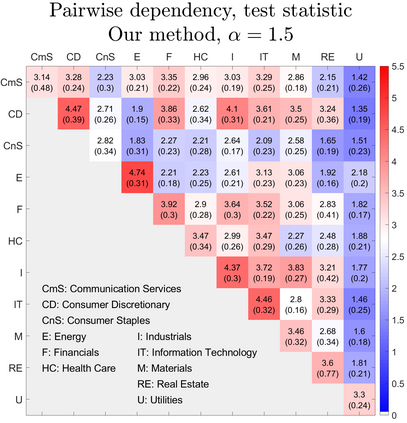
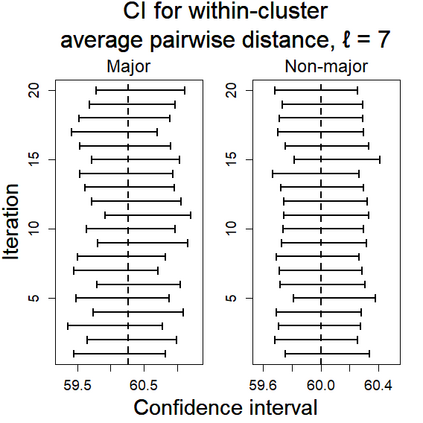
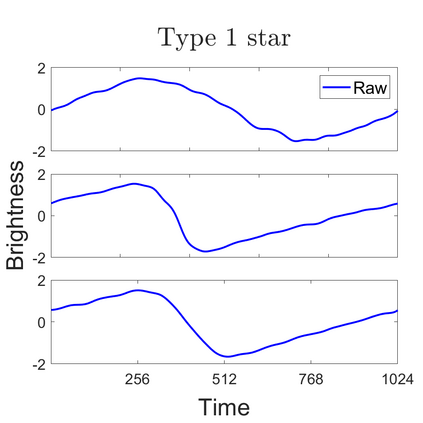
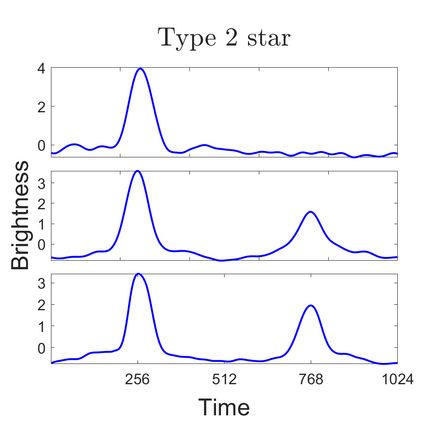
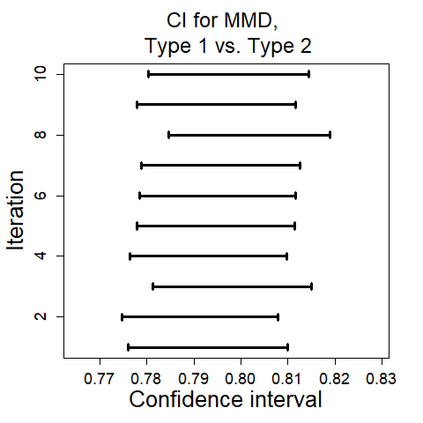
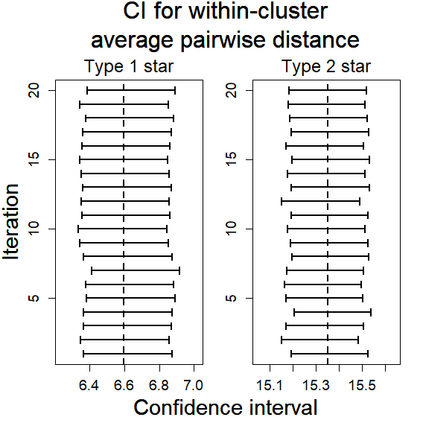
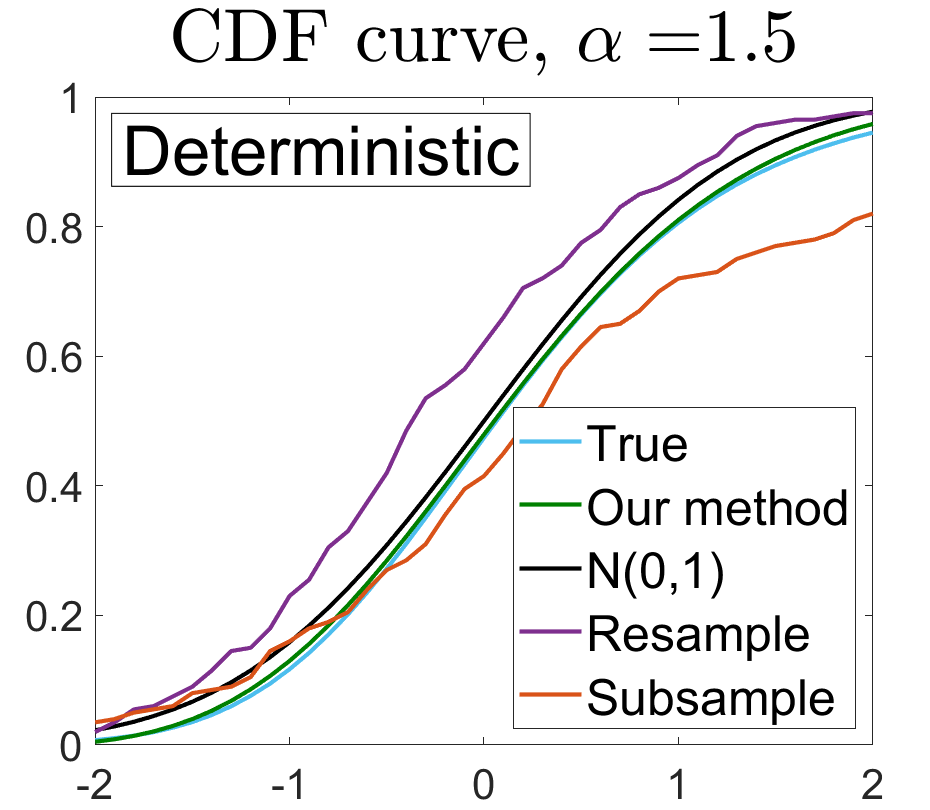
U-Statistic Reduction: Higher-Order Accurate Risk Control and Statistical-Computational Trade-Off, with Application to Network Method-of-Moments

U-statistics play central roles in many statistical learning tools but face the haunting issue of scalability. Significant efforts have been devoted into accelerating computation by U-statistic reduction. However, existing results almost exclusively focus on power analysis, while little work addresses risk control accuracy -- comparatively, the latter requires distinct and much more challenging techniques. In this paper, we establish the first statistical inference procedure with provably higher-order accurate risk control for incomplete U-statistics. The sharpness of our new result enables us to reveal how risk control accuracy also trades off with speed for the first time in literature, which complements the well-known variance-speed trade-off. Our proposed general framework converts the long-standing challenge of formulating accurate statistical inference procedures for many different designs into a surprisingly routine task. This paper covers non-degenerate and degenerate U-statistics, and network moments. We conducted comprehensive numerical studies and observed results that validate our theory's sharpness. Our method also demonstrates effectiveness on real-world data applications.