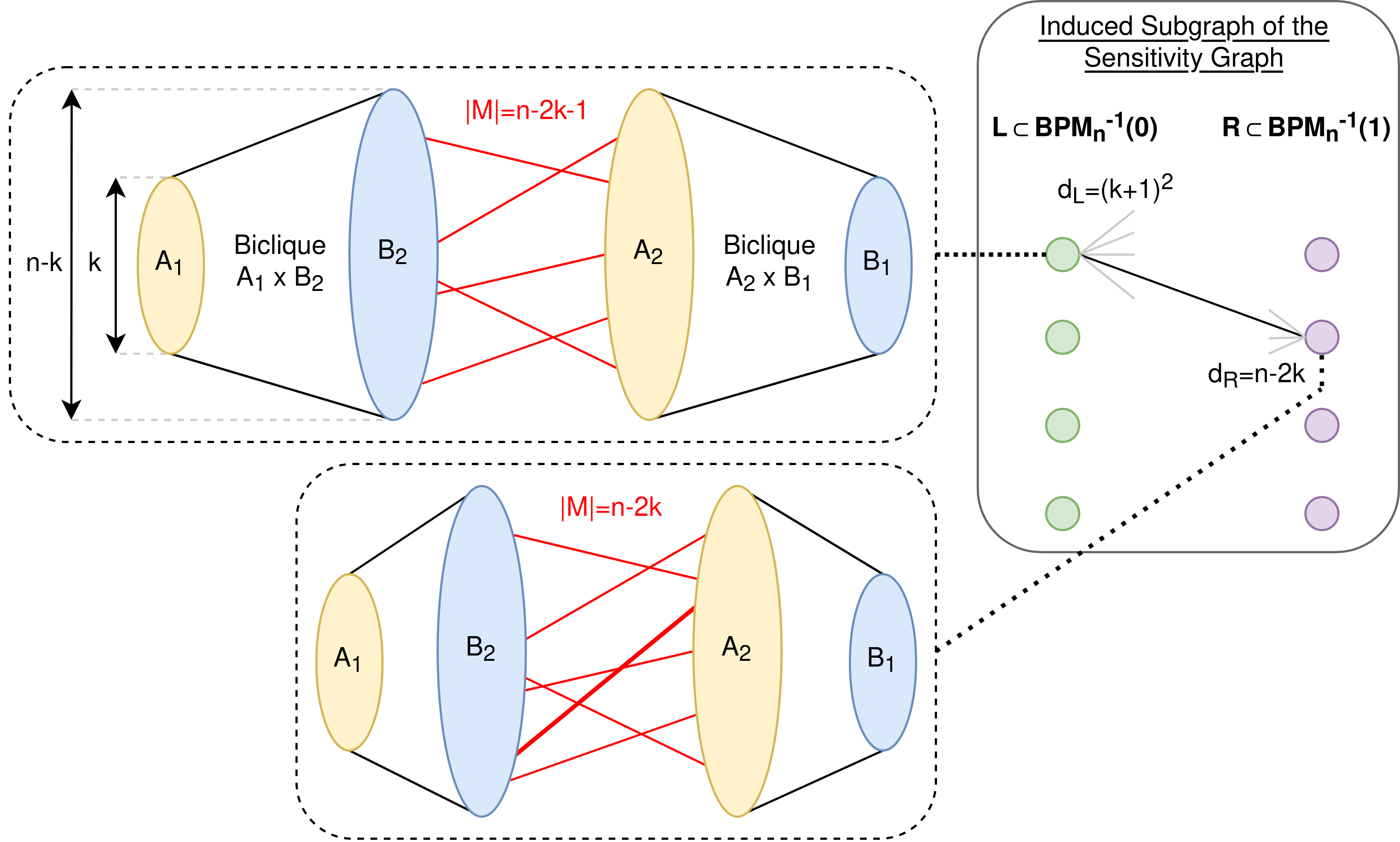
The approximate degree of a Boolean function is the least degree of a real multilinear polynomial approximating it in the $\ell_\infty$-norm over the Boolean hypercube. We show that the approximate degree of the Bipartite Perfect Matching function, which is the indicator over all bipartite graphs having a perfect matching, is $\widetilde{\Theta}(n^{3/2})$. The upper bound is obtained by fully characterizing the unique multilinear polynomial representing the Boolean dual of the perfect matching function, over the reals. Crucially, we show that this polynomial has very small $\ell_1$-norm -- only exponential in $\Theta(n \log n)$. The lower bound follows by bounding the spectral sensitivity of the perfect matching function, which is the spectral radius of its cut-graph on the hypercube \cite{aaronson2020degree, huang2019induced}. We show that the spectral sensitivity of perfect matching is exactly $\Theta(n^{3/2})$.
翻译:Boolean 超立方体上, Boolean 函数的近效度是实际的多线性多元接近度的最小值。 我们显示, Bipartite 完美匹配函数的近度是所有极匹配的双部分图形的指数 $\ loblytilde {theta} (n ⁇ 3/2}) 。 上界是通过充分描述代表完美匹配函数的布尔值双倍的独一多线性多元性来获得的。 奇怪的是, 我们显示, 多元匹配的光谱敏感度非常小 $\ ell_ 1美元- 诺姆 -- 只有 $\ Theta (n\log n) 的指数值。 下界是将完美匹配功能的光谱敏感度捆绑在一起, 这是超立管\ cite {aronson2020 度, 光度, hurang2019) 。 我们显示, 完美匹配的光谱敏感度是 $\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\