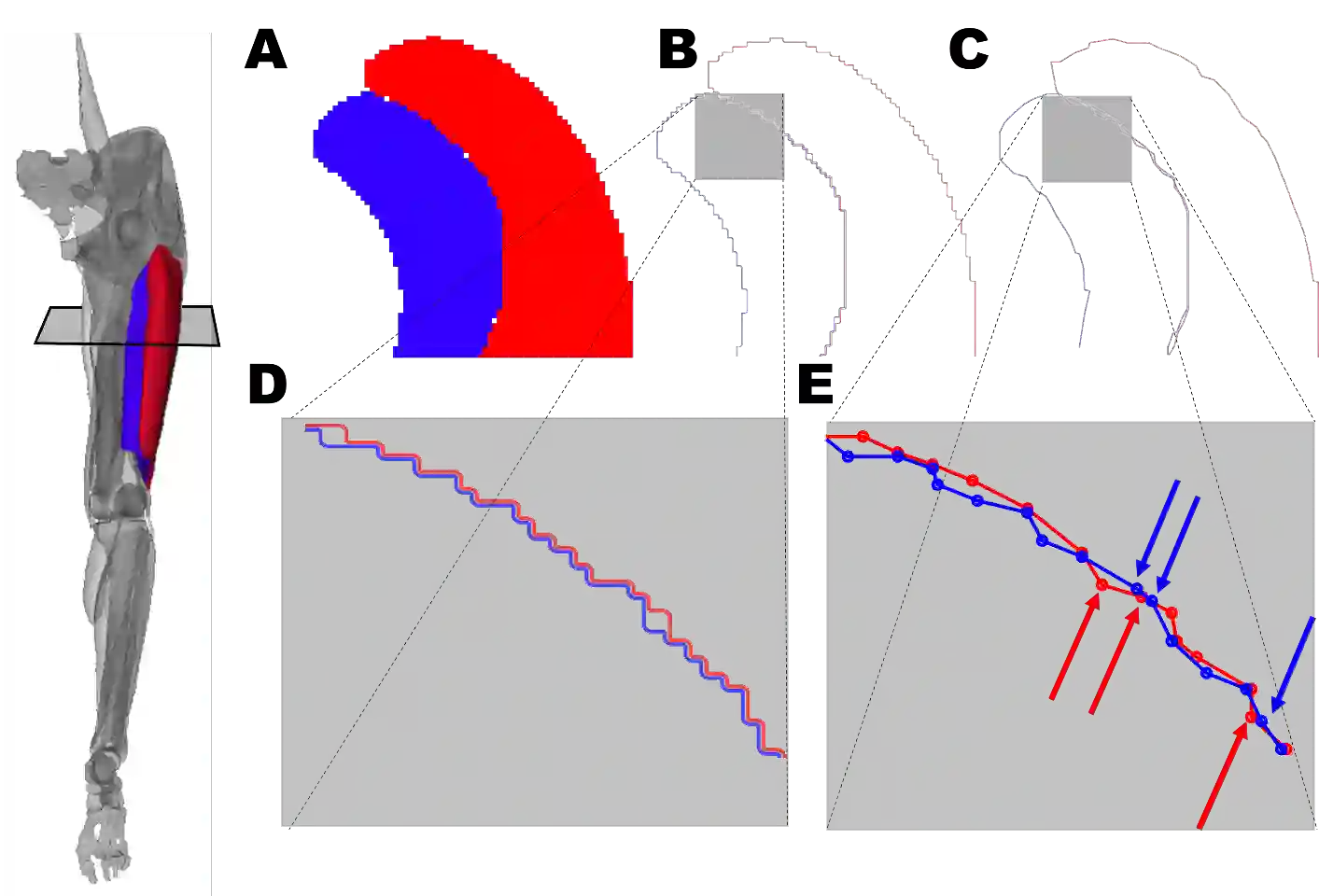
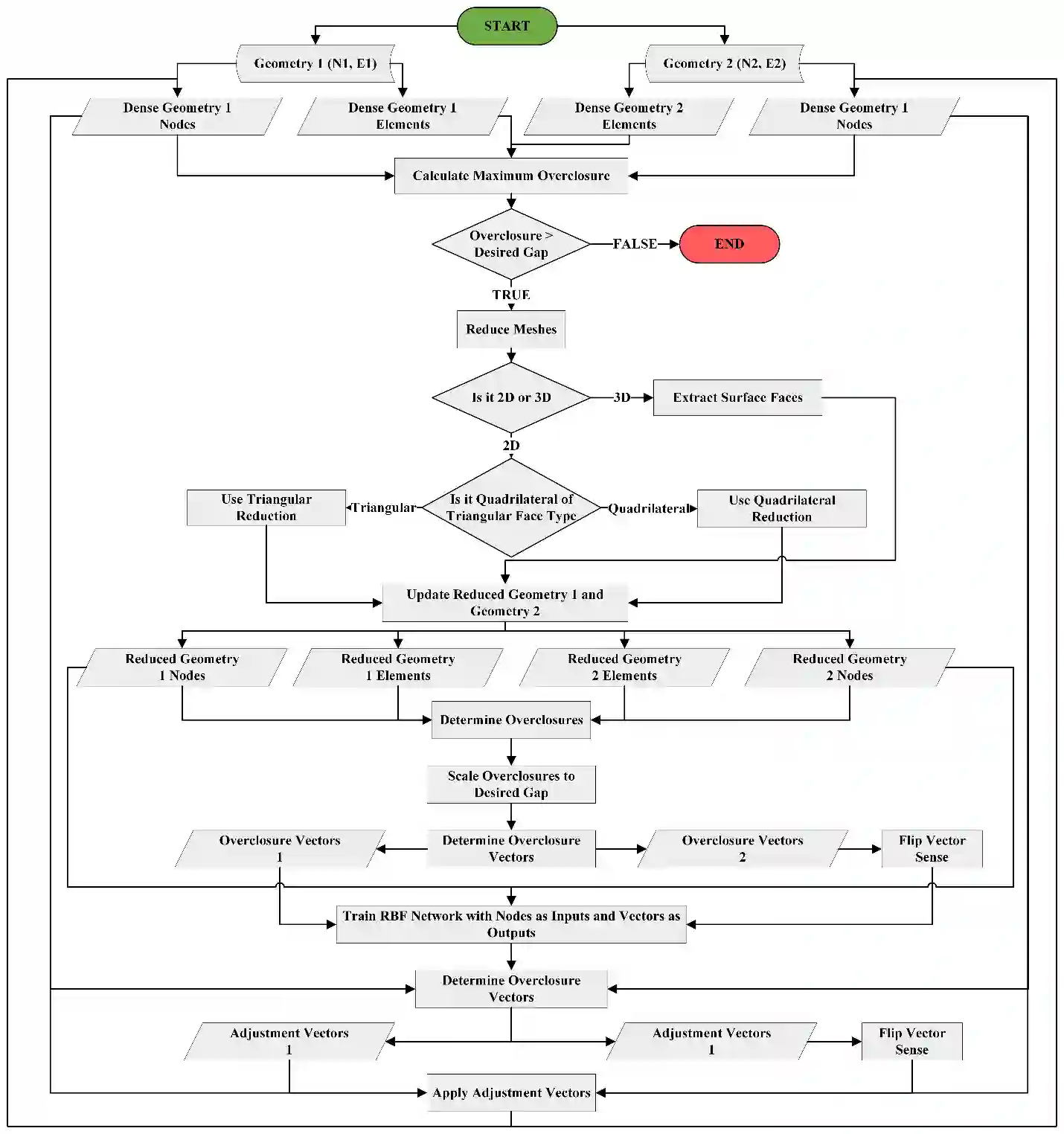
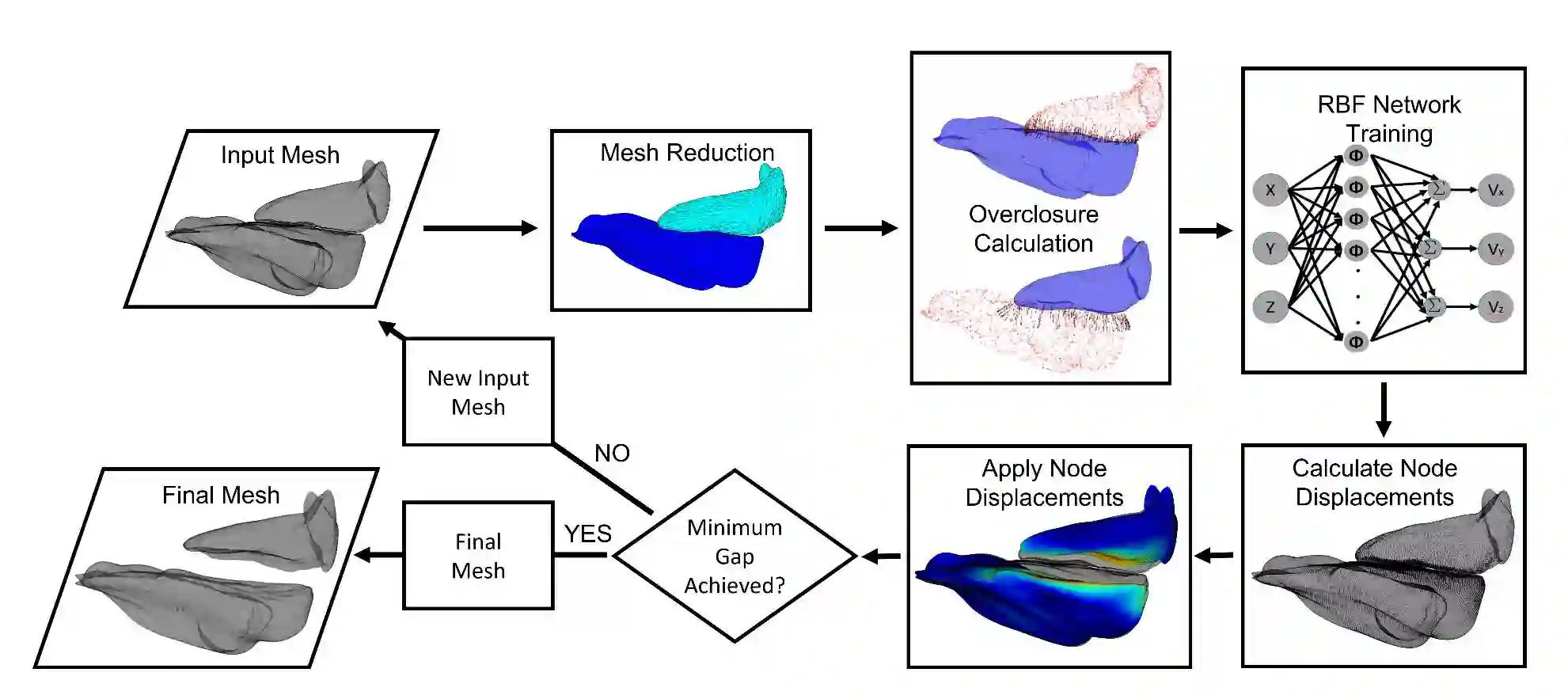
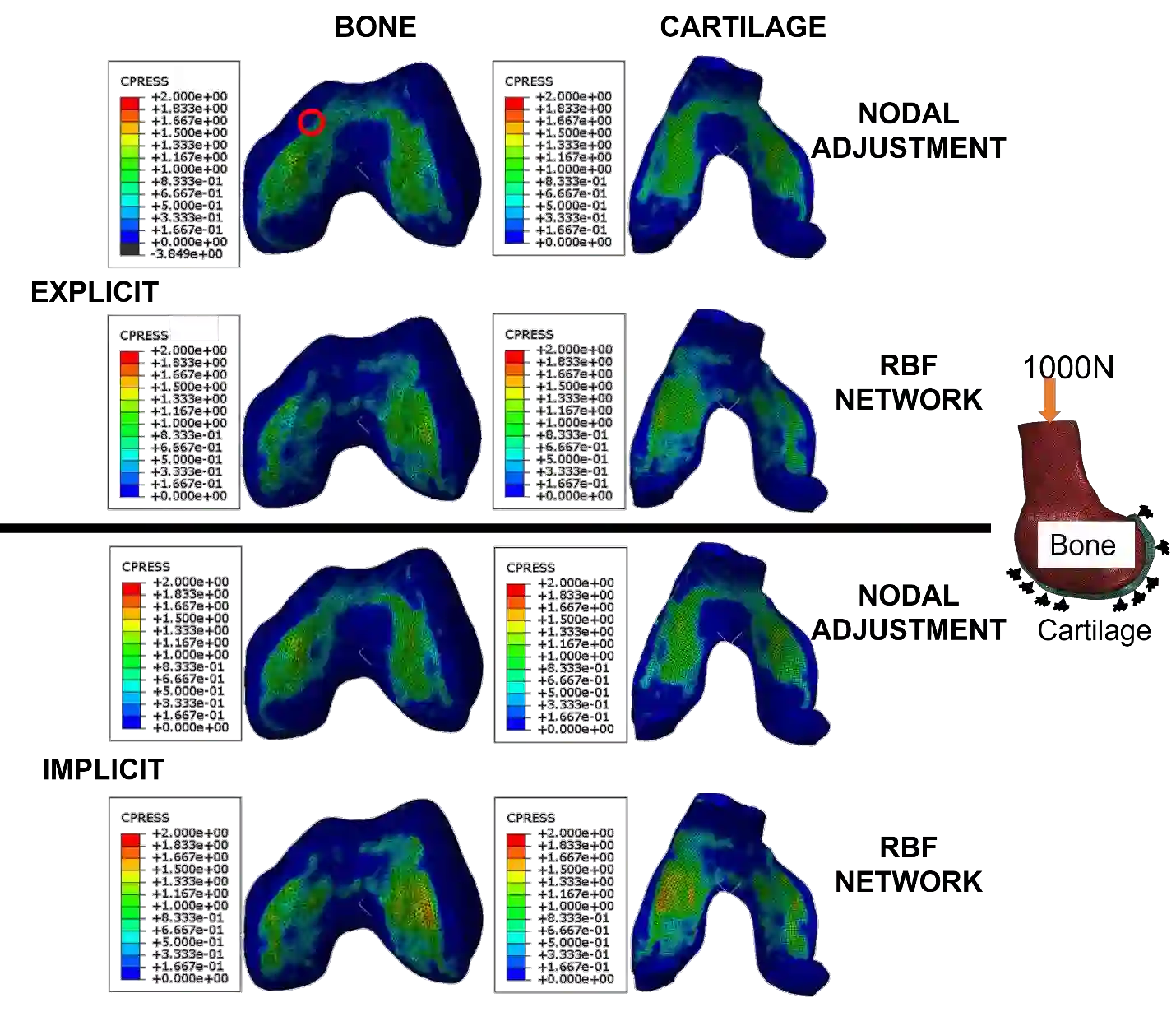
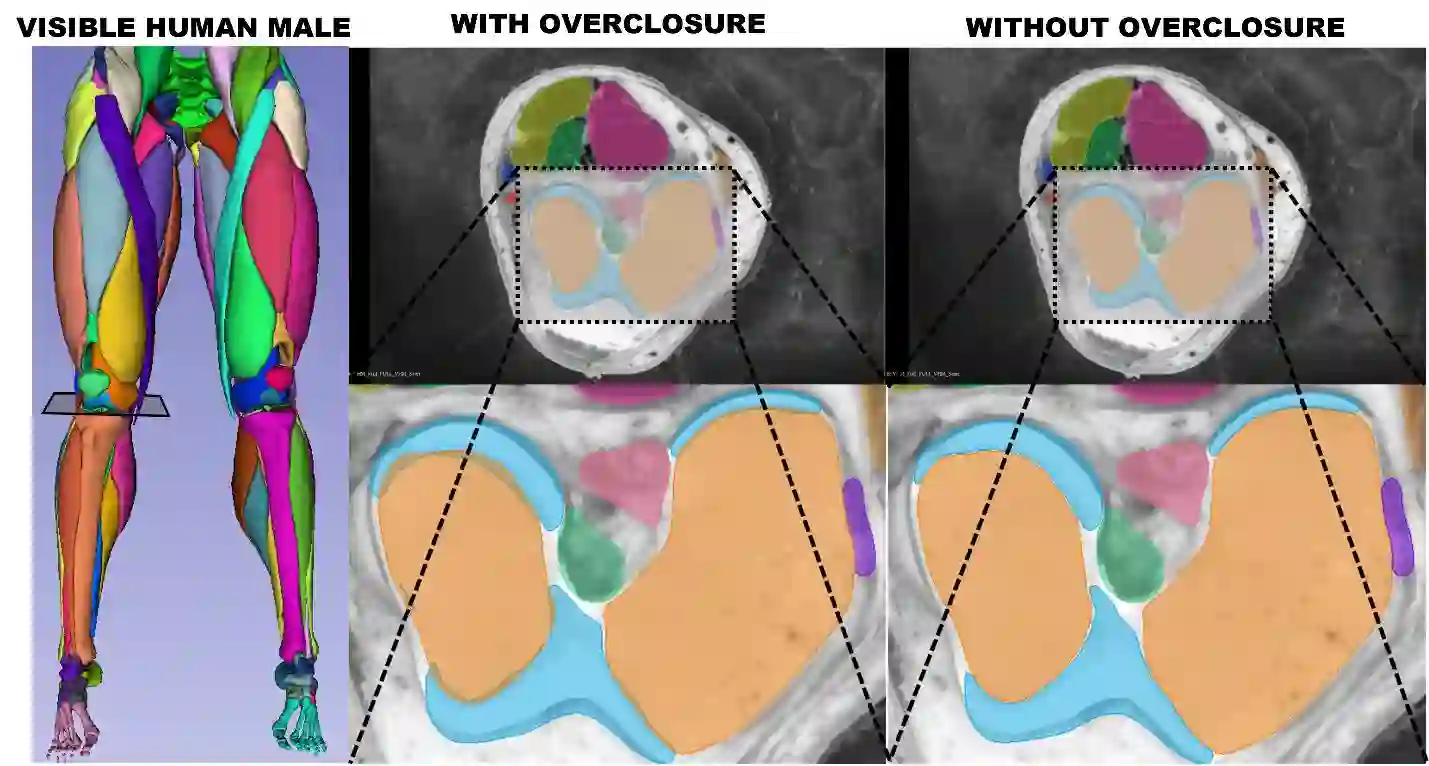
In biomechanics, geometries representing complicated organic structures are consistently segmented from sparse volumetric data or morphed from template geometries resulting in initial overclosure between adjacent geometries. In FEA, these overclosures result in numerical instability and inaccuracy as part of contact analysis. Several techniques exist to fix overclosures, but most suffer from several drawbacks. This work introduces a novel automated algorithm in an iterative process to remove overclosure and create a desired minimum gap for 2D and 3D finite element models. The RBF Network algorithm was introduced by its four major steps to remove the initial overclosure. Additionally, the algorithm was validated using two test cases against conventional nodal adjustment. The first case compared the ability of each algorithm to remove differing levels of overclosure between two deformable muscles and the effects on mesh quality. The second case used a non-deformable femur and deformable distal femoral cartilage geometry with initial overclosure to test both algorithms and observe the effects on the resulting contact FEA. The RBF Network in the first case study was successfully able to remove all overclosures. In the second case, the nodal adjustment method failed to create a usable FEA model, while the RBF Network had no such issue. This work proposed an algorithm to remove initial overclosures prior to FEA that has improved performance over conventional nodal adjustment, especially in complicated situations and those involving 3D elements. The work can be included in existing FEA modeling workflows to improve FEA results in situations involving sparse volumetric segmentation and mesh morphing. This algorithm has been implemented in MATLAB, and the source code is publicly available to download at the following GitHub repository: https://github.com/thor-andreassen/femors
翻译:在生物力学领域,代表复杂有机结构的几何体通常从稀疏体积数据中切割出来,或从模板几何体形态化,导致相邻几何体之间最初出现封闭.在有限元分析中,这些封闭会导致数值不稳定和不准确,因为这是接触分析的一部分。虽然已经存在若干修复封闭的技术,但多数存在若干缺陷.本文介绍了一种新颖的自动算法,可以通过迭代过程来移除二维和三维有限元模型的封闭,并产生所期望的最小间隙。该算法主要通过径向基函数网络介绍了四个步骤来消除最初的封闭。此外,作者们还使用两个测试用例对该算法进行了验证,对比了传统节点调整方法的效果。第一种情况下,比较了两种算法在两种内容不同的变形肌肉之间消除封闭的能力和对网格质量的影响。第二种情况下,使用具有初始封闭的不可变股骨和可变性髌骨软骨的几何形状来测试两种算法的效果,并观察电脑辅助设计的影响。第一种情况下,径向基函数网络成功地消除了所有封闭;而在第二种情况下,节点调整方法无法创建可用的有限元分析模型,而径向基函数网络却不存在这种问题。本研究提出了一种在有限元分析之前消除初始封闭的算法,它比传统节点调整方法的性能要好得多,特别是在涉及稀疏体积分割和网格形态变的复杂情况和涉及三维元素的情况下。该算法已在MATLAB中实现,源代码可以从以下GitHub存储库下载:https://github.com/thor-andreassen/femors