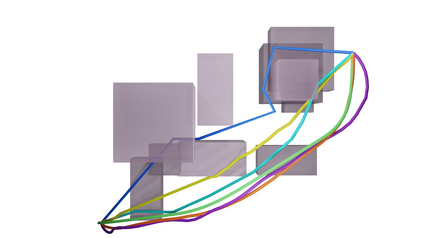
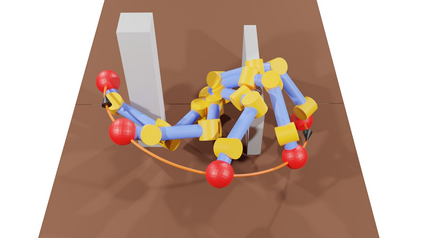
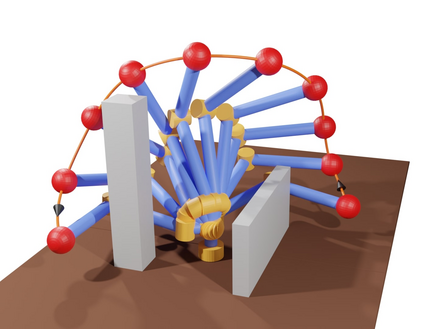
Neural Motion Planners (NMPs) have emerged as a promising tool for solving robot navigation tasks in complex environments. However, these methods often require expert data for learning, which limits their application to scenarios where data generation is time-consuming. Recent developments have also led to physics-informed deep neural models capable of representing complex dynamical Partial Differential Equations (PDEs). Inspired by these developments, we propose Neural Time Fields (NTFields) for robot motion planning in cluttered scenarios. Our framework represents a wave propagation model generating continuous arrival time to find path solutions informed by a nonlinear first-order PDE called Eikonal Equation. We evaluate our method in various cluttered 3D environments, including the Gibson dataset, and demonstrate its ability to solve motion planning problems for 4-DOF and 6-DOF robot manipulators where the traditional grid-based Eikonal planners often face the curse of dimensionality. Furthermore, the results show that our method exhibits high success rates and significantly lower computational times than the state-of-the-art methods, including NMPs that require training data from classical planners.
翻译:神经动力规划仪(NMPs)已成为在复杂环境中解决机器人导航任务的一个很有希望的工具,然而,这些方法往往需要专家的学习数据,从而限制其应用于数据生成耗时的情景。最近的事态发展还导致产生了物理学知情的深神经模型,能够代表复杂的动态部分差异。受这些动态的启发,我们提议神经时间场(NT Fields)用于在杂乱的情景中进行机器人运动规划。我们的框架代表一种波波传播模型,它产生连续到达时间,以找到由非线性第一阶PDE(称为Eikonal Equation)所通报的路径解决方案。我们评估了我们在不同封闭的3D环境中的方法,包括吉普森数据集,并展示了它解决4-DOF和6-DOF机器人操纵器的运动规划问题的能力,因为基于网络的传统Ekoonal规划师常常面临维度的诅咒。此外,结果显示,我们的方法显示成功率高,计算时间大大低于状态方法,包括需要培训古典规划数据的NMP。</s>