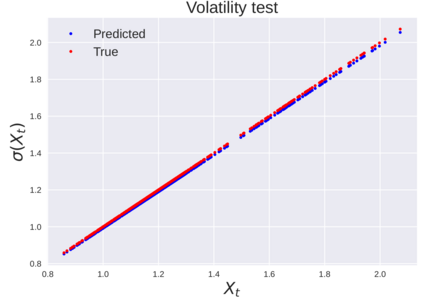
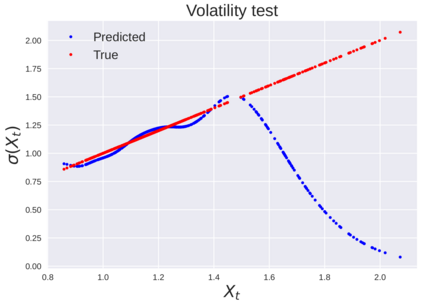
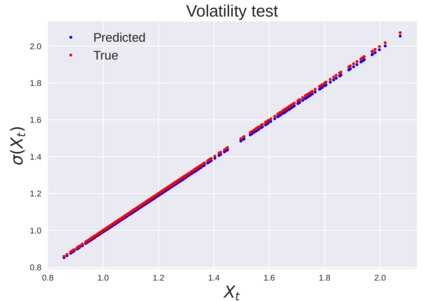
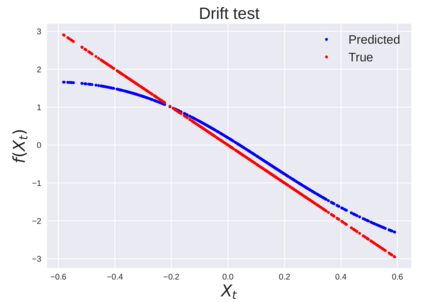
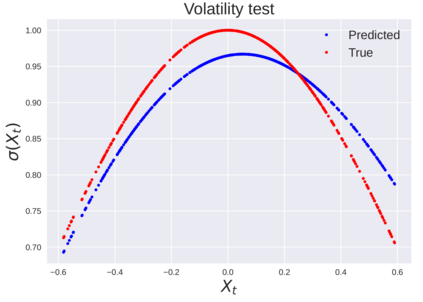
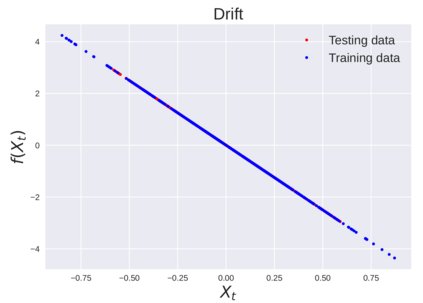
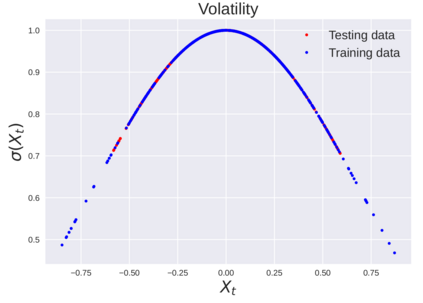
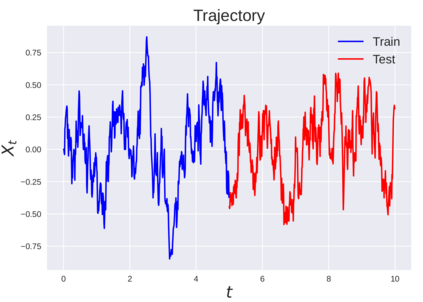
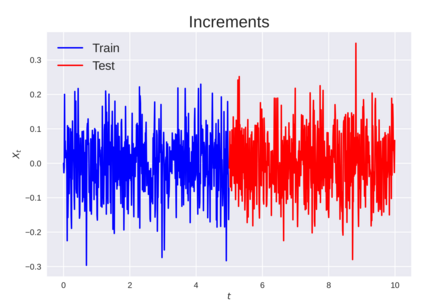
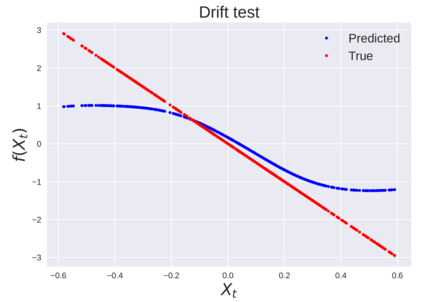
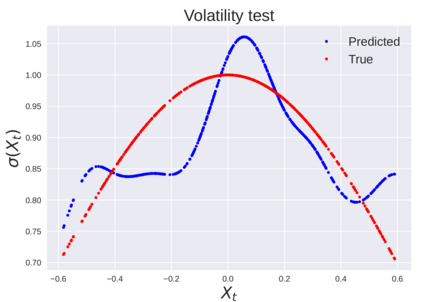
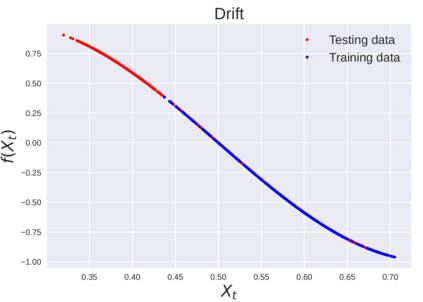
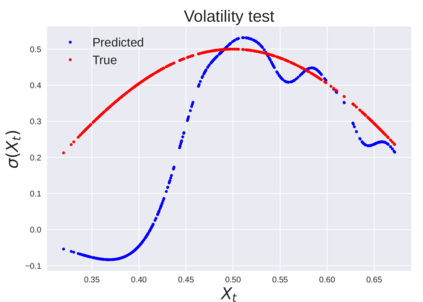
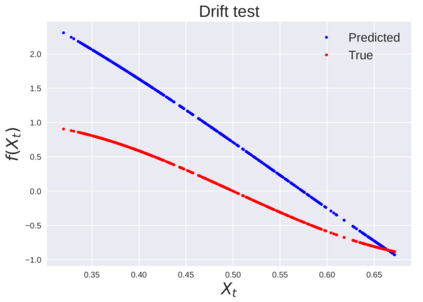
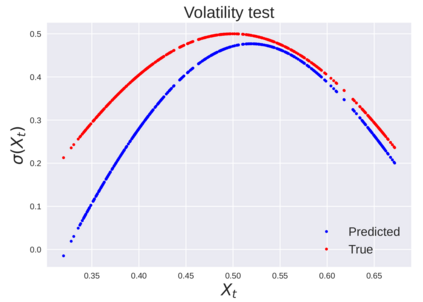
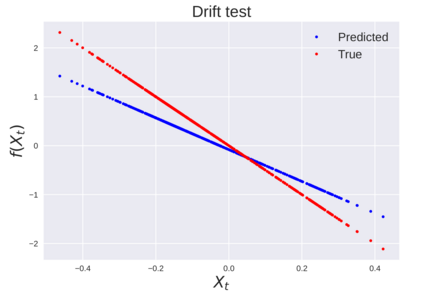
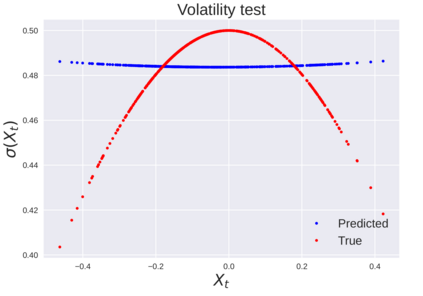
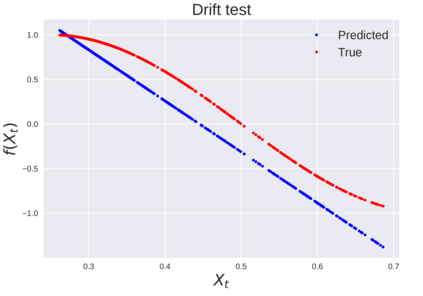
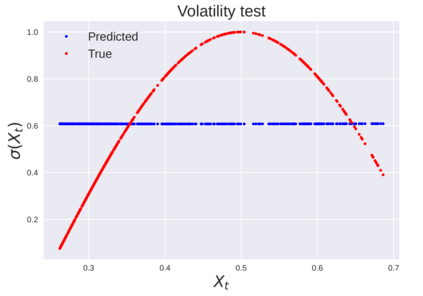
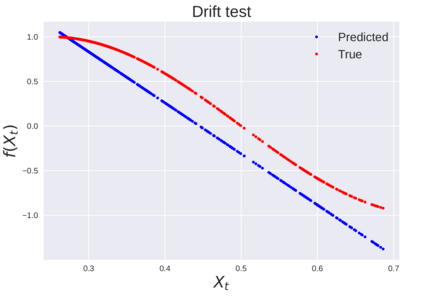
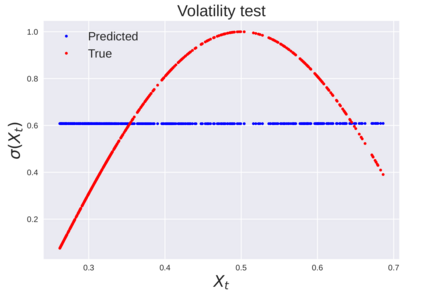
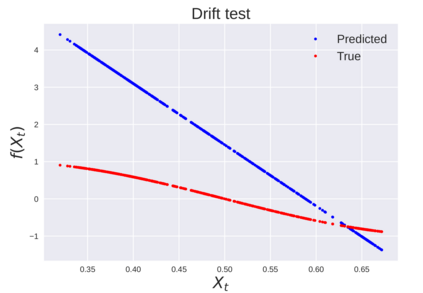
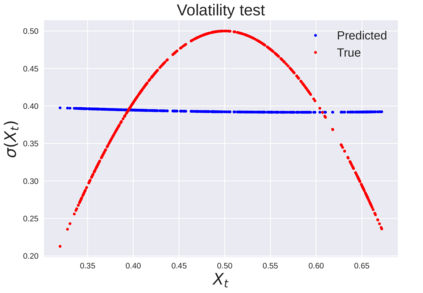
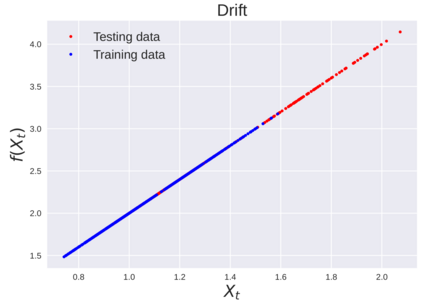
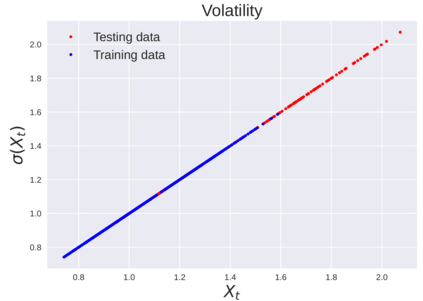
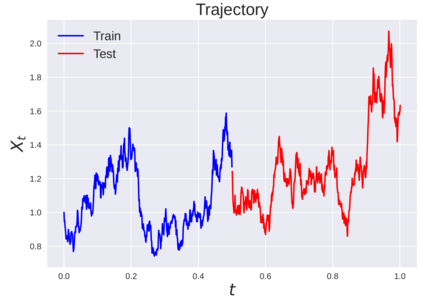
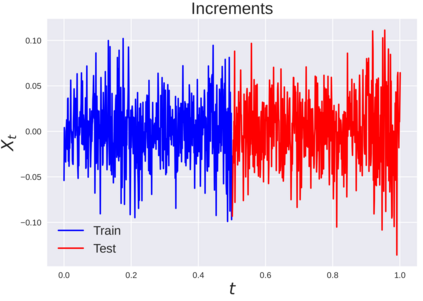
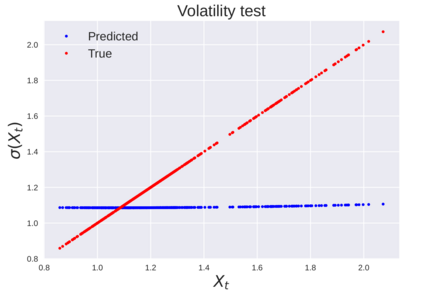
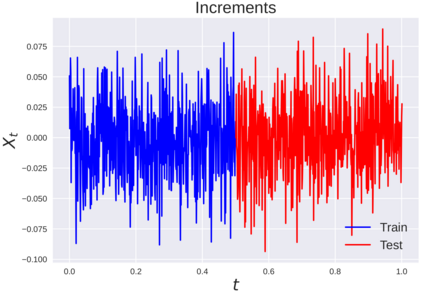
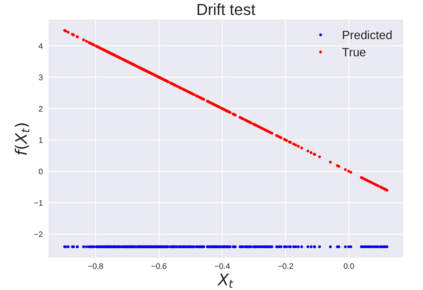
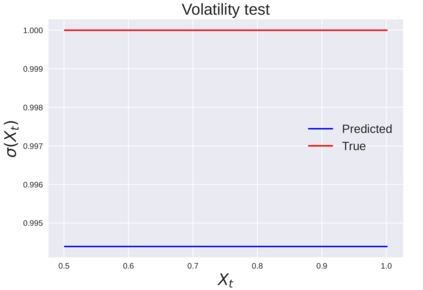
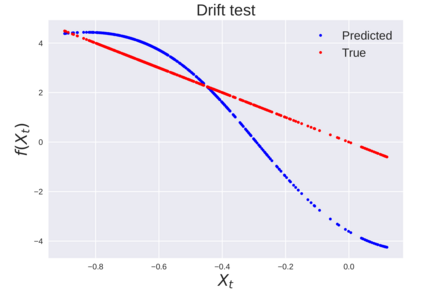
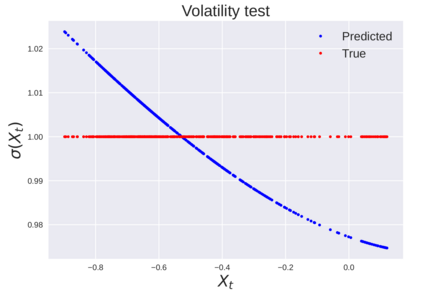
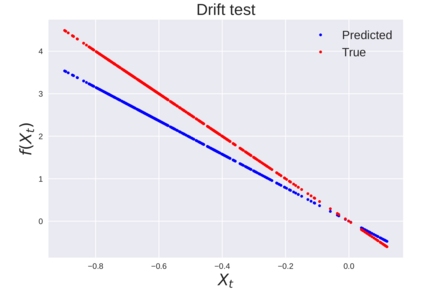
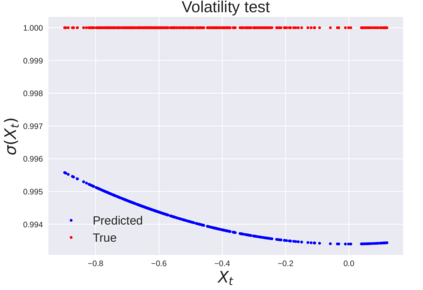
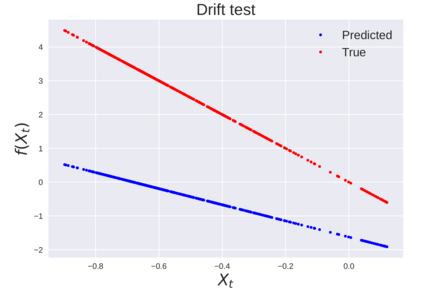
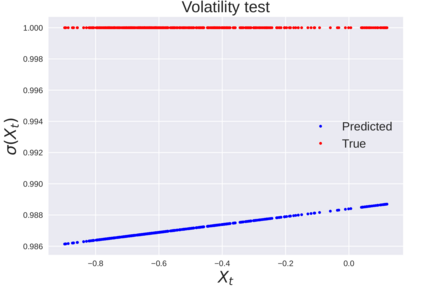
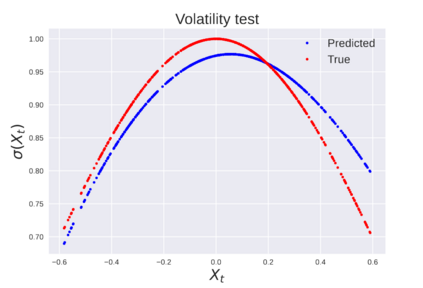
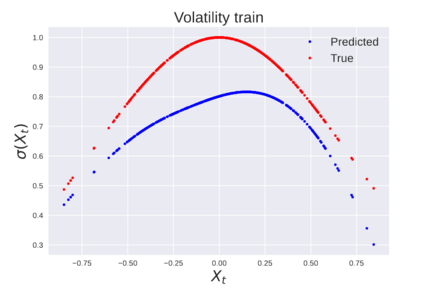
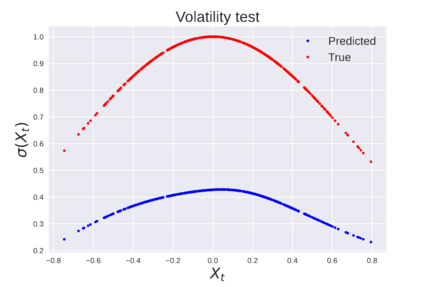
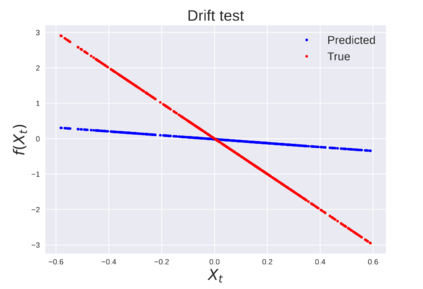
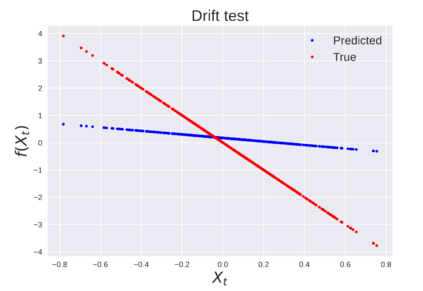
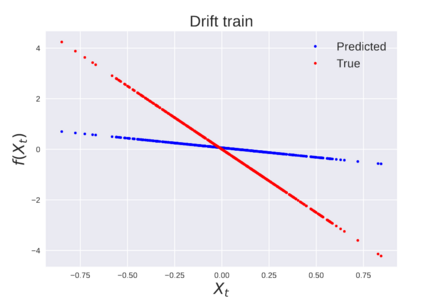
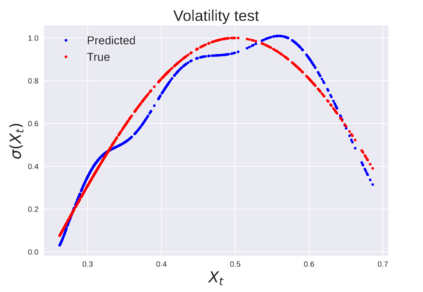
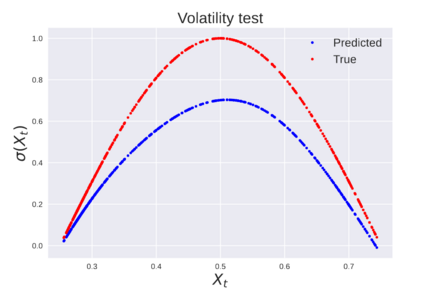
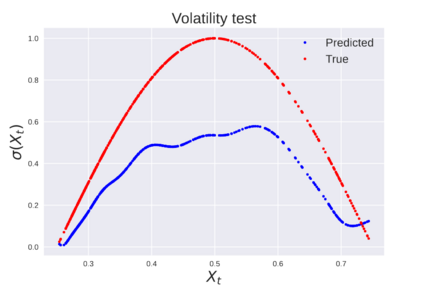
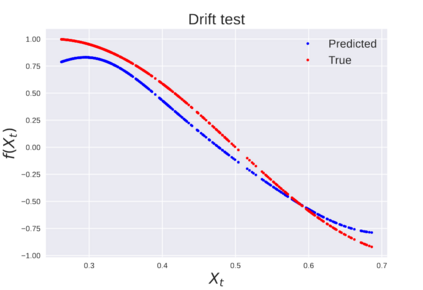
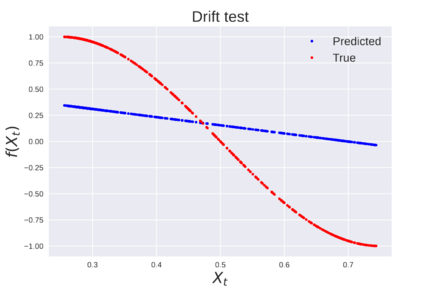
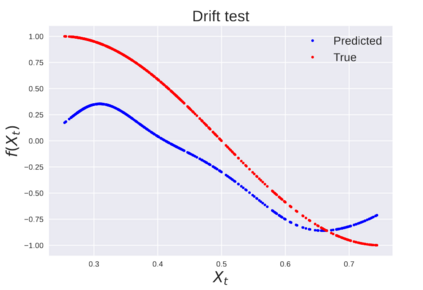
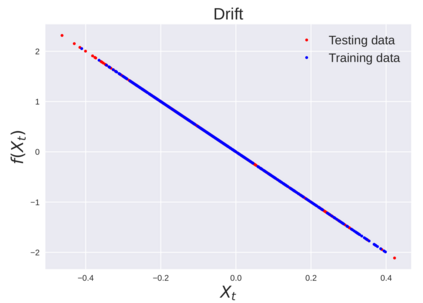
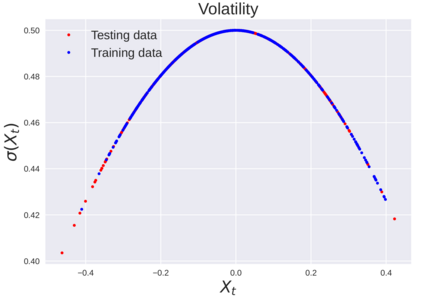
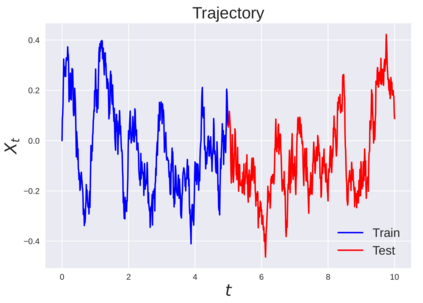
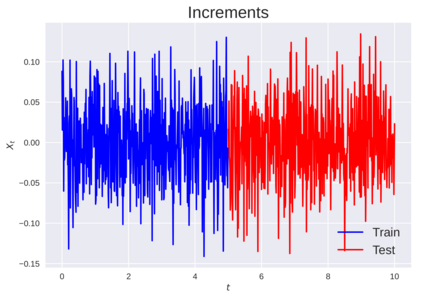
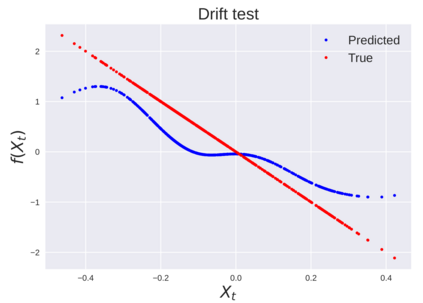
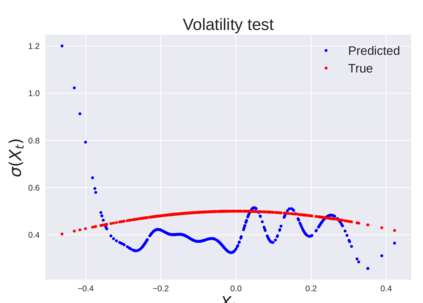
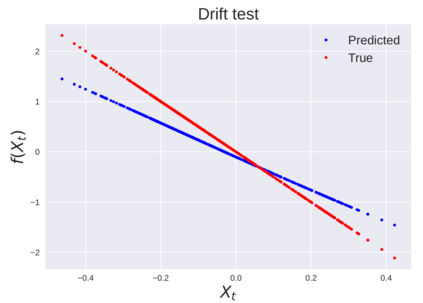
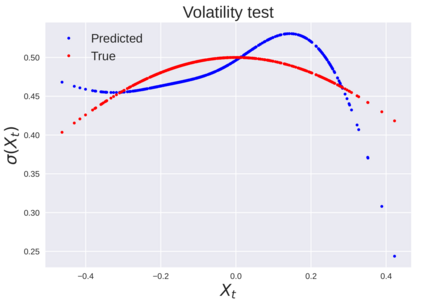
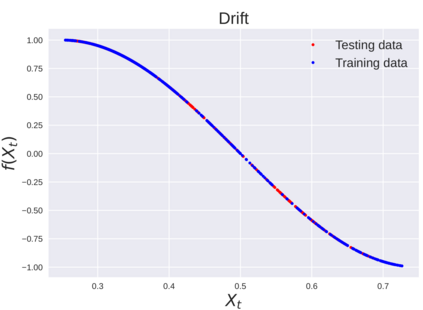
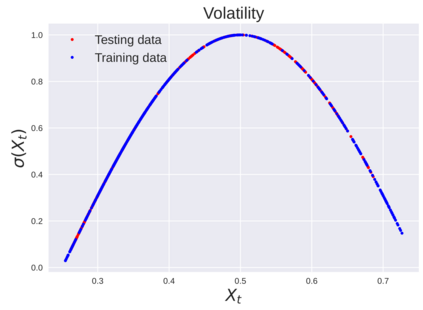
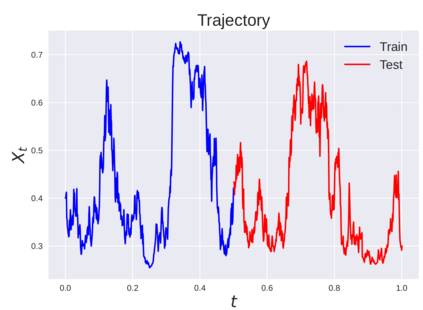
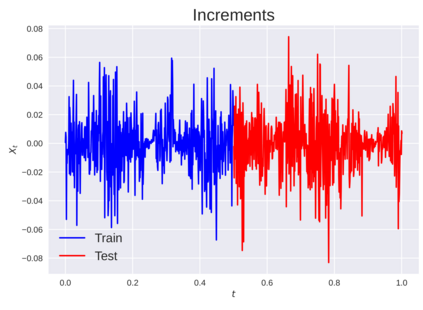
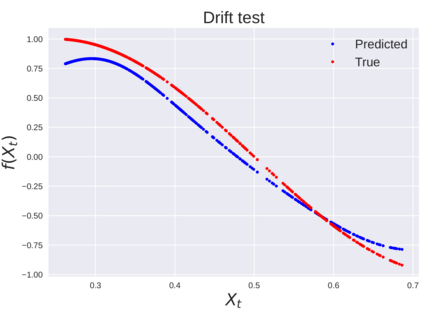
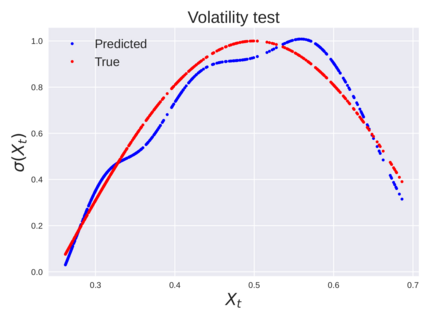
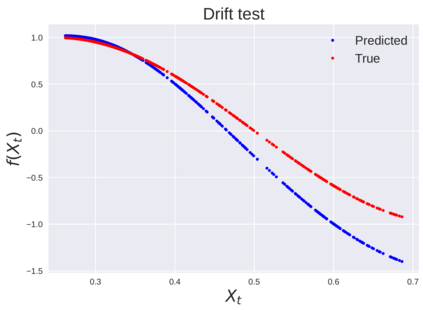
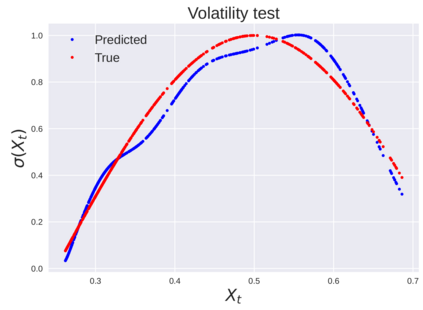
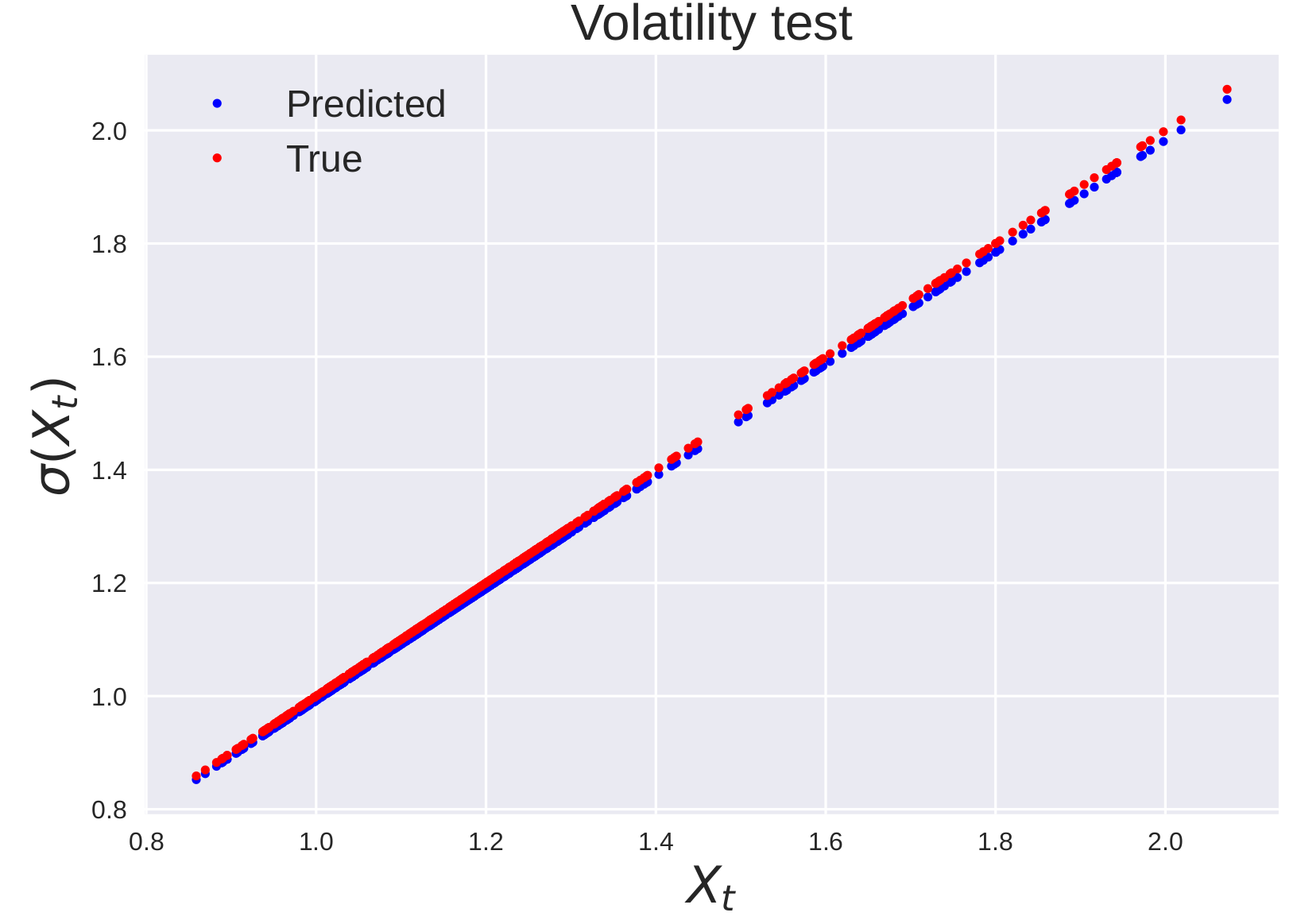
We consider the problem of learning Stochastic Differential Equations of the form $dX_t = f(X_t)dt+\sigma(X_t)dW_t $ from one sample trajectory. This problem is more challenging than learning deterministic dynamical systems because one sample trajectory only provides indirect information on the unknown functions $f$, $\sigma$, and stochastic process $dW_t$ representing the drift, the diffusion, and the stochastic forcing terms, respectively. We propose a method that combines Computational Graph Completion and data adapted kernels learned via a new variant of cross validation. Our approach can be decomposed as follows: (1) Represent the time-increment map $X_t \rightarrow X_{t+dt}$ as a Computational Graph in which $f$, $\sigma$ and $dW_t$ appear as unknown functions and random variables. (2) Complete the graph (approximate unknown functions and random variables) via Maximum a Posteriori Estimation (given the data) with Gaussian Process (GP) priors on the unknown functions. (3) Learn the covariance functions (kernels) of the GP priors from data with randomized cross-validation. Numerical experiments illustrate the efficacy, robustness, and scope of our method.
翻译:我们考虑的是从一个样本轨迹中学习 $dX_t = f(X_t)dt ⁇ sigma(X_t)dW_t 美元 。 这个问题比学习确定性动态系统更具挑战性, 因为一个样本轨迹只提供关于未知函数的间接信息 $f$, $\gma$, 以及代表漂移、扩散和随机变量的随机进程 $W_t美元。 我们建议一种方法,将计算图完成和通过新的交叉验证变式学习的数据内核结合起来。 我们的方法可以分解如下:(1) 代表时间加固图 $X_t\rightrow X ⁇ t+dt}, 因为它是一个计算图, 其中美元、 $\sgmam$和 $dWt$作为未知函数和随机变量 。 (2) 通过最高级的后加 Estruoriori Est 度(提供数据) 和前加固度数据的随机变量, 与前加固度的解算法(GP) 和前加固度的轨函数。