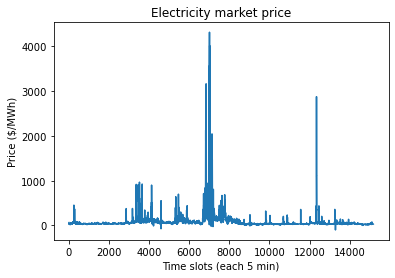
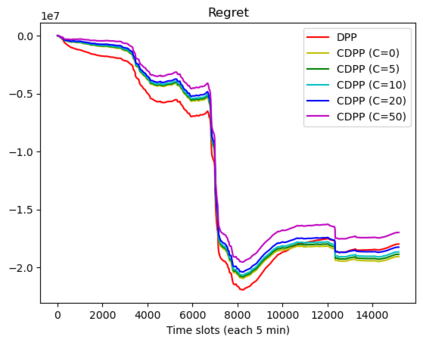
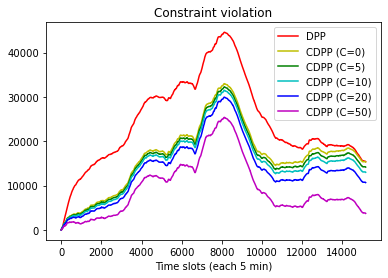
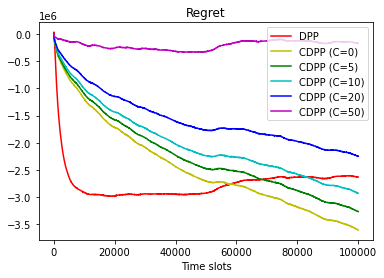
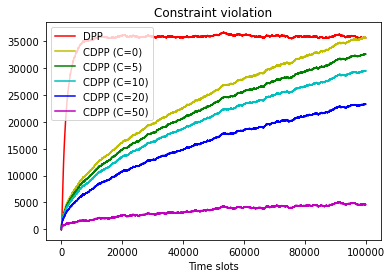
This paper studies online convex optimization with stochastic constraints. We propose a variant of the drift-plus-penalty algorithm that guarantees $O(\sqrt{T})$ expected regret and zero constraint violation, after a fixed number of iterations, which improves the vanilla drift-plus-penalty method with $O(\sqrt{T})$ constraint violation. Our algorithm is oblivious to the length of the time horizon $T$, in contrast to the vanilla drift-plus-penalty method. This is based on our novel drift lemma that provides time-varying bounds on the virtual queue drift and, as a result, leads to time-varying bounds on the expected virtual queue length. Moreover, we extend our framework to stochastic-constrained online convex optimization under two-point bandit feedback. We show that by adapting our algorithmic framework to the bandit feedback setting, we may still achieve $O(\sqrt{T})$ expected regret and zero constraint violation, improving upon the previous work for the case of identical constraint functions. Numerical results demonstrate our theoretical results.
翻译:本文在网上研究“ 软盘优化” 和“ 软盘限制” 。 我们提出一个替代的“ 软盘- 软盘- 软盘” 算法, 保证在固定的迭代次数后, 将预期的遗憾和零约束违反额($O)( sqrt{T}) 用于改善香草漂流- 软盘方法($O)(sqrt{T}) 的违反。 我们的算法与香草流- 软盘- 软盘方法相反, 忽略了时间范围($T) 。 这是基于我们的新颖的“ 漂流 Lemma ” 算法, 提供了虚拟队列漂移的时间轮圈, 从而导致虚拟队列长度的反常线。 此外, 我们扩展了我们的框架, 在两点带宽的反馈下, 以随机调节的在线锥盘优化。 我们通过调整我们的算法框架来适应“ 硬盘反馈设置 ”, 我们仍可以实现“ $(\ qrt{T) 的预期的“ 硬盘和零约束 ” 。