Generative Adversarial Equilibrium Solvers

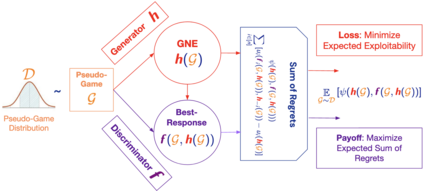
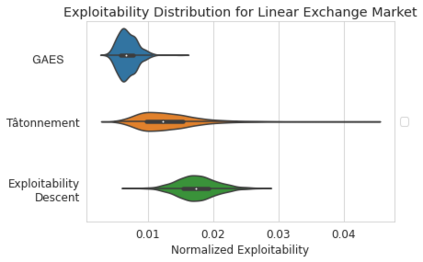
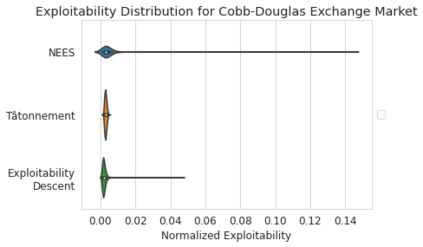
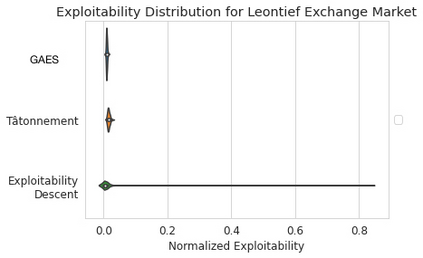
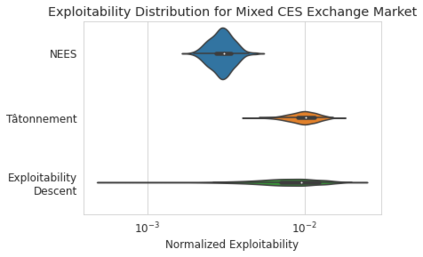
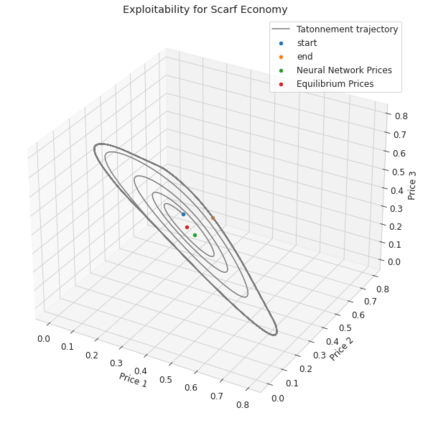
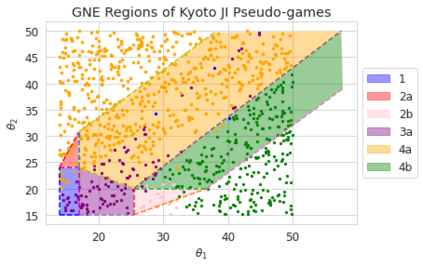
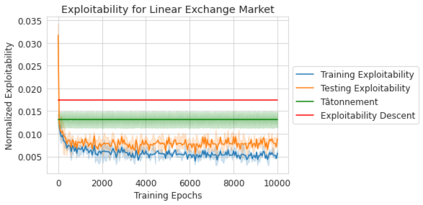
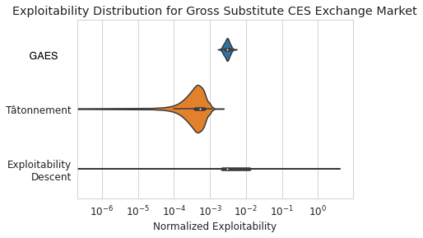
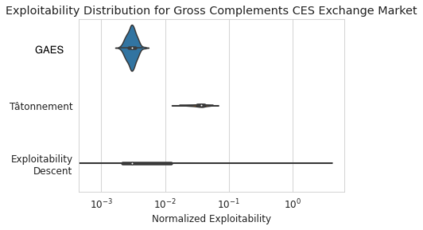
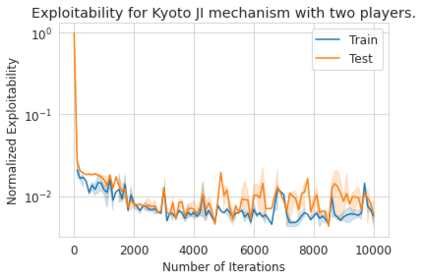
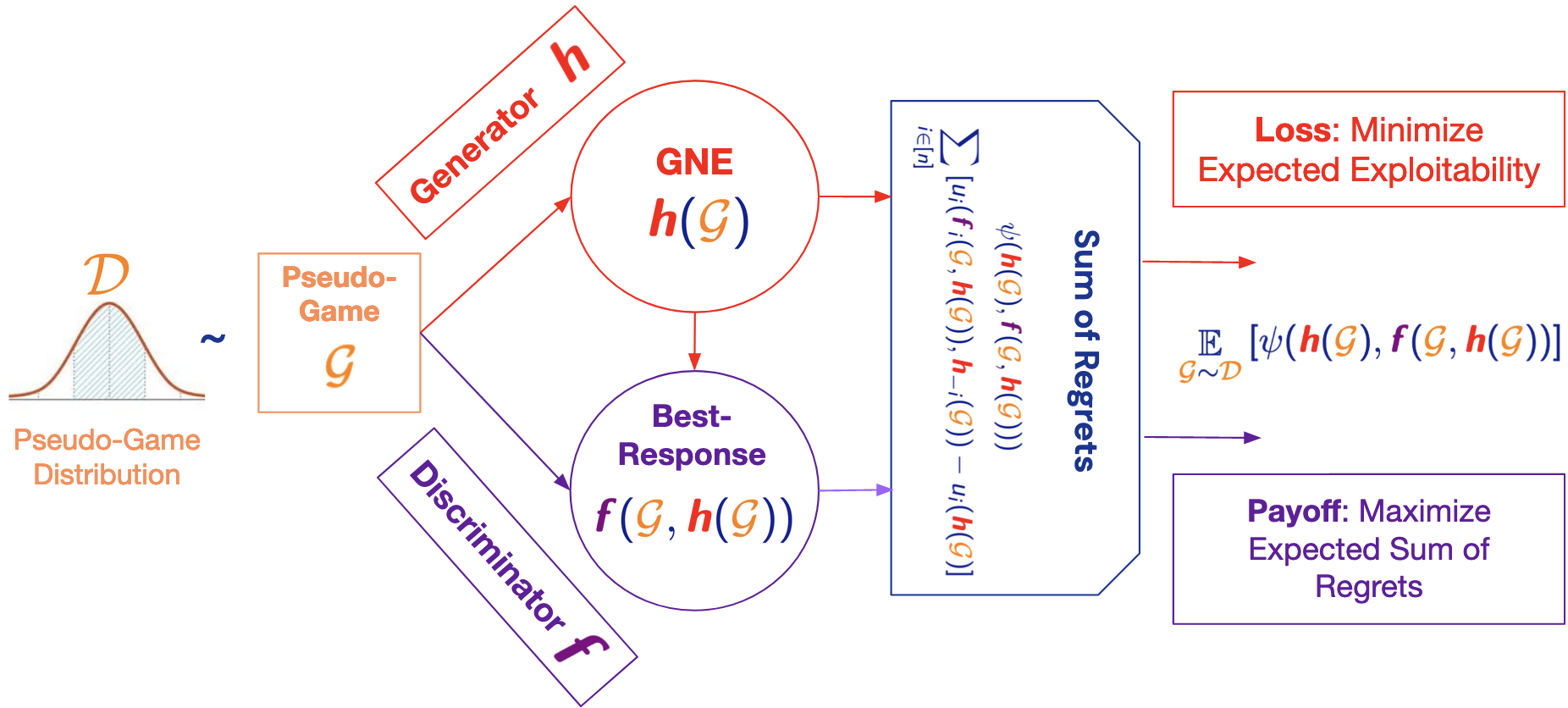
We introduce the use of generative adversarial learning to compute equilibria in general game-theoretic settings, specifically the \emph{generalized Nash equilibrium} (GNE) in \emph{pseudo-games}, and its specific instantiation as the \emph{competitive equilibrium} (CE) in Arrow-Debreu competitive economies. Pseudo-games are a generalization of games in which players' actions affect not only the payoffs of other players but also their feasible action spaces. Although the computation of GNE and CE is intractable in the worst-case, i.e., PPAD-hard, in practice, many applications only require solutions with high accuracy in expectation over a distribution of problem instances. We introduce Generative Adversarial Equilibrium Solvers (GAES): a family of generative adversarial neural networks that can learn GNE and CE from only a sample of problem instances. We provide computational and sample complexity bounds, and apply the framework to finding Nash equilibria in normal-form games, CE in Arrow-Debreu competitive economies, and GNE in an environmental economic model of the Kyoto mechanism.