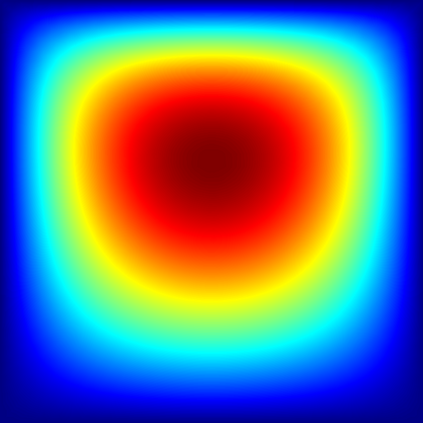
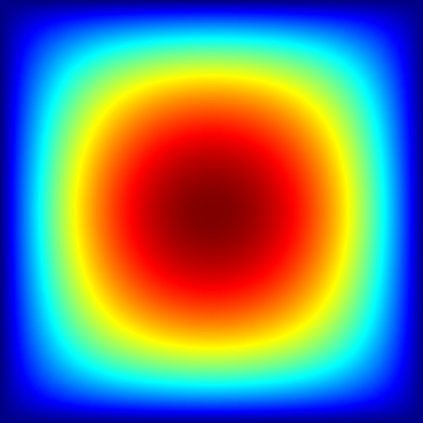
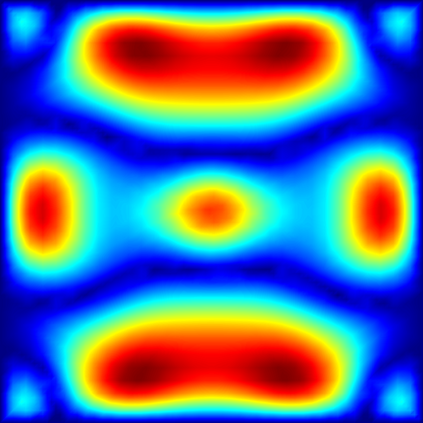
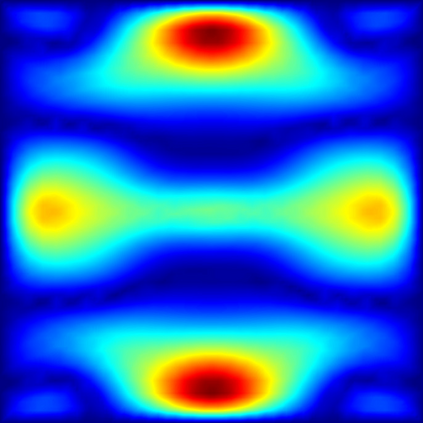
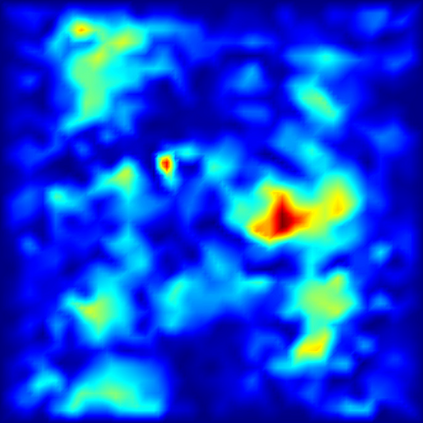
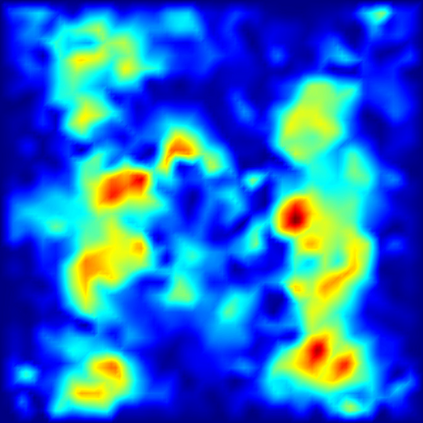
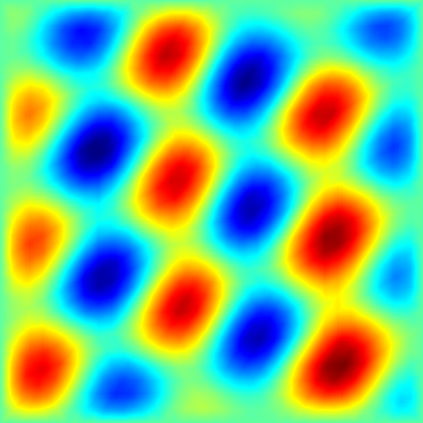
We develop the uniform sparse Fast Fourier Transform (usFFT), an efficient, non-intrusive, adaptive algorithm for the solution of elliptic partial differential equations with random coefficients. The algorithm is an adaption of the sparse Fast Fourier Transform (sFFT), a dimension-incremental algorithm, which tries to detect the most important frequencies in a given search domain and therefore adaptively generates a suitable Fourier basis corresponding to the approximately largest Fourier coefficients of the function. The usFFT does this w.r.t. the stochastic domain of the PDE simultaneously for multiple fixed spatial nodes, e.g., nodes of a finite element mesh. The key idea of joining the detected frequency sets in each dimension increment results in a Fourier approximation space, which fits uniformly for all these spatial nodes. This strategy allows for a faster and more efficient computation due to a significantly smaller amount of samples needed, than just using other algorithms, e.g., the sFFT for each spatial node separately. We test the usFFT for different examples using periodic, affine and lognormal random coefficients in the PDE problems.
翻译:我们开发了统一的稀有快速傅里叶变换(usFFT),这是一个高效的、非侵入性的、适应性的算法,用于解决具有随机系数的椭圆部分方程。算法是稀有的快速傅里叶变换(sFFT)的适配法,这是一种维度进化的算法,它试图在特定的搜索域中探测最重要的频率,因此适应性地生成一个与功能中大约最大的四里叶系数相对应的合适的四里叶基。UsFFT同时使用这个 w.r.t.PDE的随机域,用于多个固定的空间节点,例如,定点元素网格的节点。将每个维度增量中测到的频率组合合并到一个四里叶相近空格中,这个关键想法对所有空间节点都是一致的。这个策略使得可以更快和更有效地计算出所需的样本数量要大大小得多,而不只是使用其他算法,例如每个空间节点的SFFT。我们测试了我们FFT在PDE问题中使用的定期、亲和逻辑随机随机系数的不同例子。