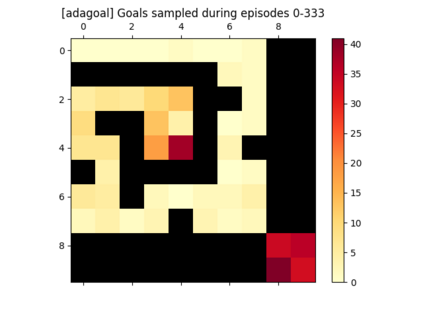
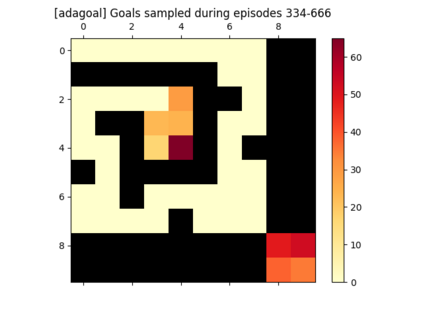
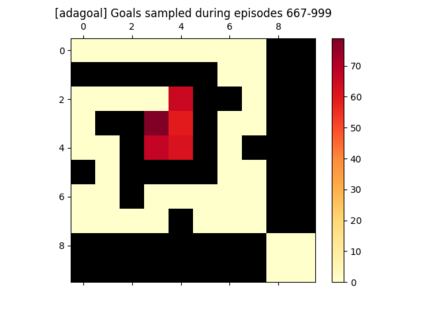
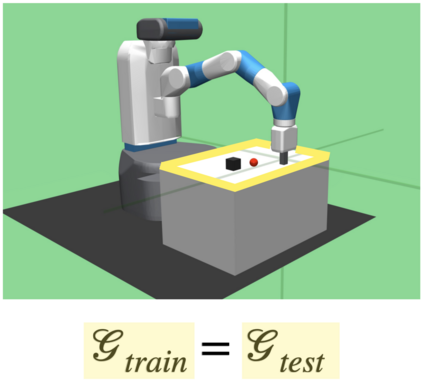
We introduce a generic strategy for provably efficient multi-goal exploration. It relies on AdaGoal, a novel goal selection scheme that leverages a measure of uncertainty in reaching states to adaptively target goals that are neither too difficult nor too easy. We show how AdaGoal can be used to tackle the objective of learning an $\epsilon$-optimal goal-conditioned policy for the (initially unknown) set of goal states that are reachable within $L$ steps in expectation from a reference state $s_0$ in a reward-free Markov decision process. In the tabular case with $S$ states and $A$ actions, our algorithm requires $\tilde{O}(L^3 S A \epsilon^{-2})$ exploration steps, which is nearly minimax optimal. We also readily instantiate AdaGoal in linear mixture Markov decision processes, yielding the first goal-oriented PAC guarantee with linear function approximation. Beyond its strong theoretical guarantees, we anchor AdaGoal in goal-conditioned deep reinforcement learning, both conceptually and empirically, by connecting its idea of selecting "uncertain" goals to maximizing value ensemble disagreement.
翻译:我们引入了一种通用战略,用于效率高的多目标探索。它依赖于Ada目标,这是一个新颖的目标选择计划,它利用了一定的不确定性,使各国达到适应性目标的目标,既不太困难,也不过于容易。我们展示了如何利用Ada目标实现以下目标的目标:学习一套(最初未知的)目标中以美元为最佳目标条件的美元政策,这一套目标要求从参考状态的0.0美元到无报酬的Markov决定程序中的预期以美元为单位的以美元为单位。在以美元为单位的国家和以美元为单位的表格中,我们的算法需要美元(L3S A\epsillon%2})为单位的探索步骤,这几乎是最低的。我们还在线性混合的Markov决策过程中将选择“稳定的分歧”目标的Ada目标与线性功能的近似值联系起来,从而产生第一个以目标为导向的PAC保证。除了强有力的理论保证外,我们还将Ada目标化的深度强化学习,无论是在概念上还是实验上,通过将其选择“可达到的最高价值”的目标性目标性目标性目标性目标性目标性目标性目标性目标性目标性目标性目标联系起来。