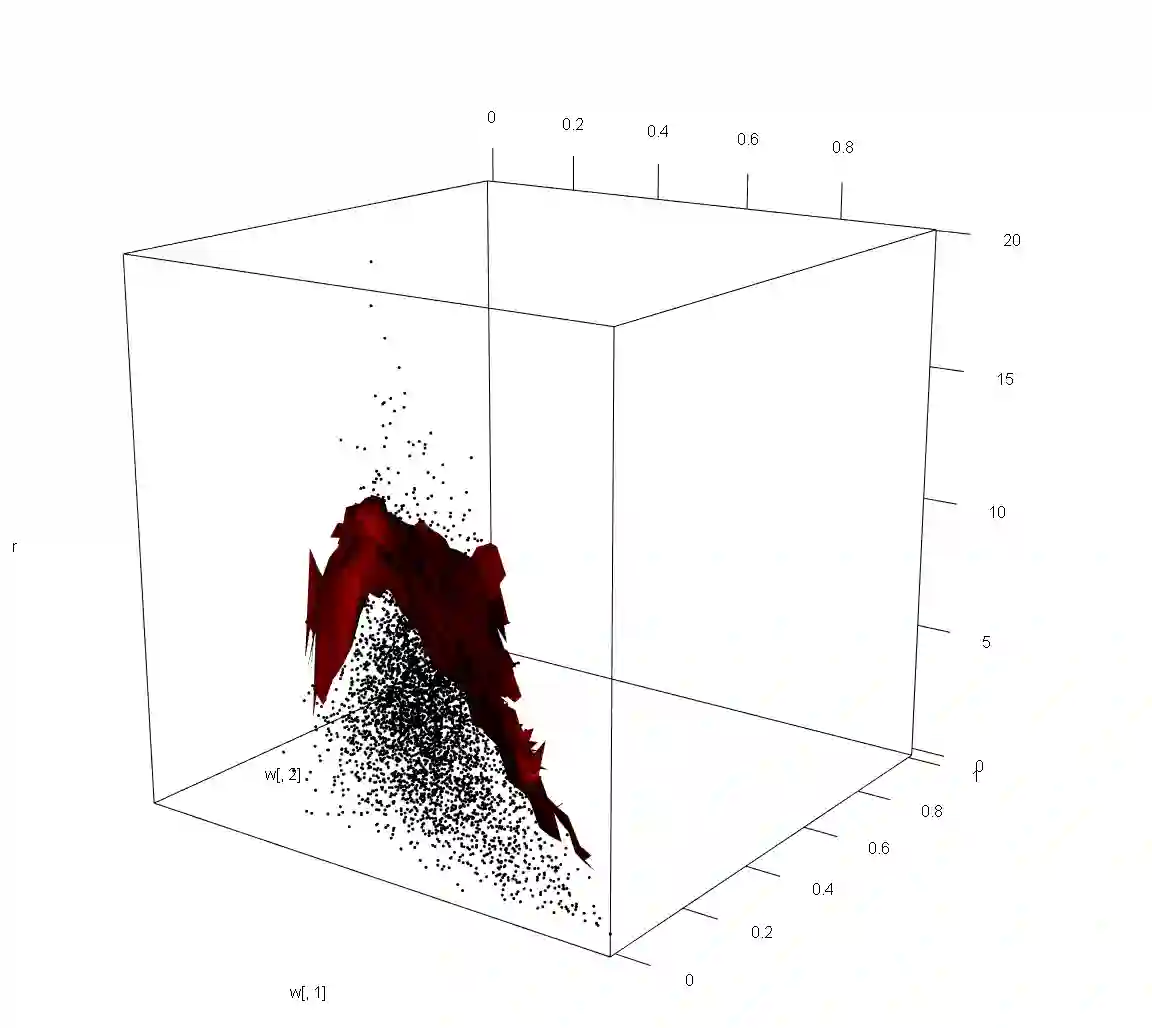
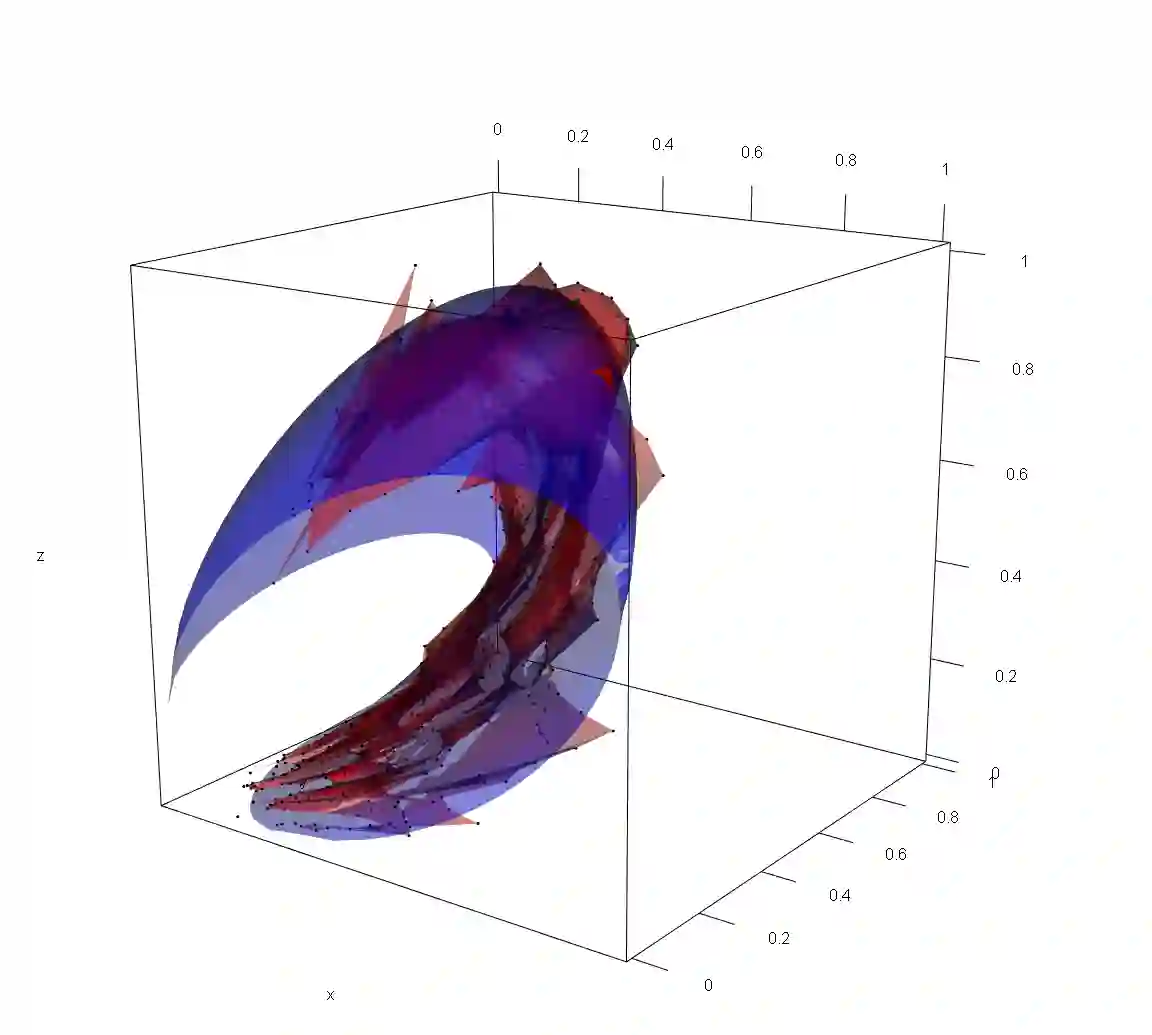
A geometric representation for multivariate extremes, based on the shapes of scaled sample clouds in light-tailed margins and their so-called limit sets, has recently been shown to connect several existing extremal dependence concepts. However, these results are purely probabilistic, and the geometric approach itself has not been fully exploited for statistical inference. We outline a method for parametric estimation of the limit set shape, which includes a useful non/semi-parametric estimate as a pre-processing step. More fundamentally, our approach provides a new class of asymptotically-motivated statistical models for the tails of multivariate distributions, and such models can accommodate any combination of simultaneous or non-simultaneous extremes through appropriate parametric forms for the limit set shape. Extrapolation further into the tail of the distribution is possible via simulation from the fitted model. A simulation study confirms that our methodology is very competitive with existing approaches, and can successfully allow estimation of small probabilities in regions where other methods struggle. We apply the methodology to two environmental datasets, with diagnostics demonstrating a good fit.
翻译:多变极端的几何表示方式,其依据是光尾边边和所谓的限数组中按比例浮云的形状,最近显示它连接了几个现有的极端依赖性概念;然而,这些结果纯属概率性,而且没有充分利用几何方法本身来进行统计推断。我们概述了一套极限形状的参数估计方法,其中包括作为预处理步骤的有用的非/半参数估计。更根本地说,我们的方法为多变分布的尾部提供了一种新的零星动力统计模型,这种模型可以通过限制形状的适当参数形式容纳同时或非同时极极端的任何组合。通过模拟模型的模拟,可以进一步推断分布的尾部。模拟研究证实,我们的方法与现有方法非常有竞争力,并能够成功地估计其他方法挣扎的区域的小概率。我们对两种环境数据集应用了这种方法,诊断显示非常合适。