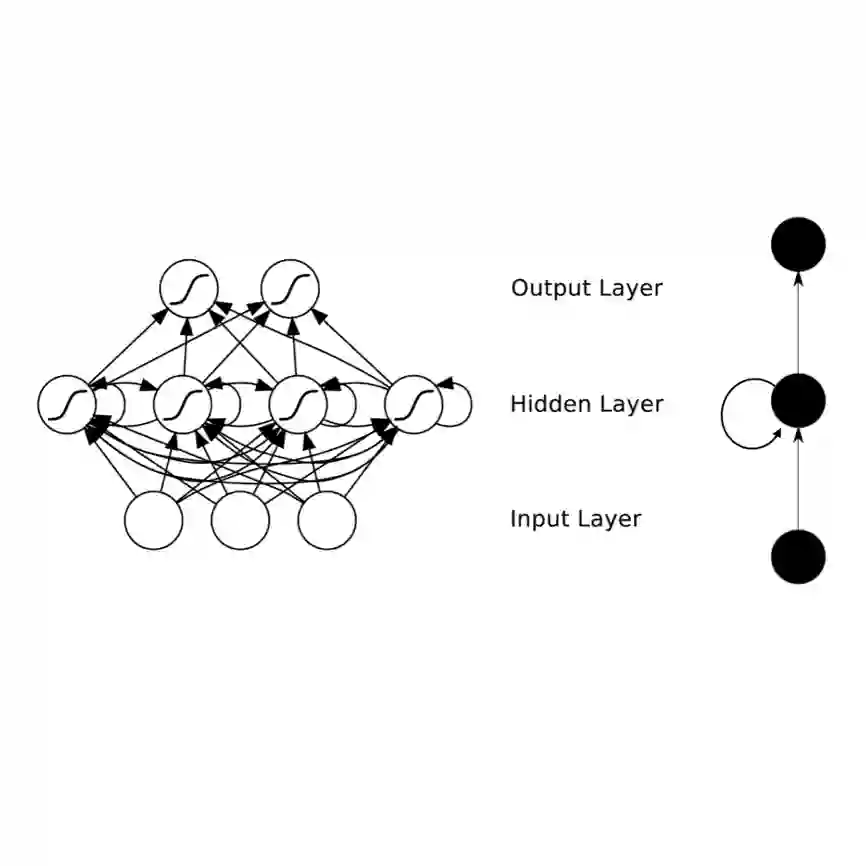
A Pseudo-Random Number Generator (PRNG) is any algorithm generating a sequence of numbers approximating properties of random numbers. These numbers are widely employed in mid-level cryptography and in software applications. Test suites are used to evaluate PRNGs quality by checking statistical properties of the generated sequences. These sequences are commonly represented bit by bit. This paper proposes a Reinforcement Learning (RL) approach to the task of generating PRNGs from scratch by learning a policy to solve a partially observable Markov Decision Process (MDP), where the full state is the period of the generated sequence and the observation at each time step is the last sequence of bits appended to such state. We use a Long-Short Term Memory (LSTM) architecture to model the temporal relationship between observations at different time steps, by tasking the LSTM memory with the extraction of significant features of the hidden portion of the MDP's states. We show that modeling a PRNG with a partially observable MDP and a LSTM architecture largely improves the results of the fully observable feedforward RL approach introduced in previous work.
翻译:Pseudo-random 数字生成器(PRNG) 是产生随机数字接近数字属性序列的任何算法。 这些数字在中层加密和软件应用中被广泛使用。 测试套套用于通过检查生成序列的统计属性来评估 PLNG的质量。 这些序列通常以位数表示 。 本文建议用强化学习( RL) 方法从零开始生成PRNG的任务, 学习一项政策来解决部分可见的Markov 决策过程( MDP ), 其中, 完整的状态是生成序列的时期, 并且每个步骤的观测是该状态的最后一序列。 我们使用一个长期短期内存( LSTM) 结构来模拟不同时间步骤的观测之间的时间关系, 将 LSTM 记忆与提取 MDP 状态隐藏部分的重要特征进行任务。 我们显示, 以部分可见的 MDP 和 LSTM 结构为模型, 大大改进了先前工作中引入的完全可观测的 RL 方法的结果 。